高三第一学期期中数学考试卷（理科）(5)
一、填空题（每题6分，共84分）
1、设P、Q为两个非空实数集合，定义集合
若P＝{－1，0，1}，Q＝{－2，2}，则 集合P·Q中元素的个数是___________
2、已知命题
，命题p的否定为命题q，则q是“
”；q的真假为 （填真，假）。
3、已知f(x)=log2x，则
4、已知a,b为常数，若
，则5a-b= ;
5、设周期函数
是定义在R上的奇函数，若的最小正周期为3，且
，
，则m的取值范围是
;
6、设
，
是两个不共线的向量，若
，
，
，且
三点共线，则
_______
7、已知
则当mn取得最小值时，椭圆
的离心率是___________
8、已知
，则
的值为_____________
|
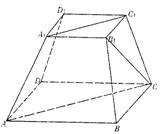
下底面边长为2，高为1，则直线B1C与面ACC1A1所成角
的正切值是 .
10、图中阴影部分的面积为__________。
11、过抛物线
与抛物线交于A、B两点，且△OAB（O为坐标原点）的面积为
=
.
12、9．已知不等式
对任意正实数x，y恒成立，则正实数a的最小值是_______________
13、给出下列四个命题：
①若
②若
③若
④
的最小值为9.
其中正确命题的序号是 .
14、给出以下几个命题：
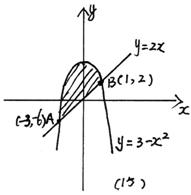
①由曲线y=x2与直线y=2x围成的封闭区域的面积为
.
②已知点A是定圆C上的一个定点，线段AB为圆的动弦，若
，O为坐标原点，则动点P的轨迹为圆；
③把5本不同的书分给4个人，每人至少1本，则不同的分法种数为A54·A41=480种.
④若直线l//平面α，直线l⊥直线m，直线
平面β，则β⊥α，
其中正确命题的序号是 .
二、解答题：（本大题共6小题，共76分）
15、（本小题满分12分）已知a、b、c是△ABC三边长，关于x的方程
的两根之差的平方等于4，△ABC的面积
（Ⅰ）求角C；（Ⅱ）求a、b的值.
16、（本小题满分12分）
已知数列{an}的前n项和为Sn，且满足
（Ⅰ）判断
是否为等差数列？并证明你的结论；
（Ⅱ）求Sn和an
| |
17、（本小题满分12分）甲、乙两公司同时开发同一种新产品，经测算，对于函数f（x）、g（x），当甲公司投入x万元作宣传时，若乙公司投入的宣传费小于f（x）万元，则乙公司对这一新产品的开发有失败的风险，否则没有失败的风险；当乙公司投入x万元作宣传时，若甲公司投入的宣传费小于g（x）万元，则甲公司对这一新产品的开发有失败的风险，否则没有失败的风险。
（Ⅰ）试解释
的实际意义；
（Ⅱ）设
，甲、乙公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能少地投入宣传费用，问甲、乙两公司各应投入多少宣传费？
18、（本小题满分12分）已知函数
，曲线
在点x=1处的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为
，若
时，
有极值．
(I) 求a、b、c的值；
(II) 求在[-3,1]上的最大值和最小值．
19、（本小题满分14分）（普通班学生做） 已知函数
，设
，
（1）求
，
的表达式，并猜想
的表达式（直接写出猜想结果）
（2）若关于
的函数
在区间
上的最小值为6，求
的值。
20、（本小题满分14分）（普通班学生做）在平面直角坐标系xoy中，直线l与抛物线
相交于不同的A、B两点.
（Ⅰ）如果直线l过抛物线的焦点，求
的值；
（Ⅱ）如果
证明直线l必过一定点，并求出该定点.
19、（本小题满分14分）（实验班学生做）已知二次函数
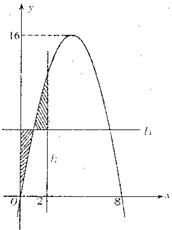
为常数）；
.若直线l1、l2与函数f（x）的图象以及l1，y轴与函数f（x）的图象所围成的封闭图形如阴影所示.
（Ⅰ）求a、b、c的值
（Ⅱ）求阴影面积S关于t的函数S（t）的解析式；
|
问是否存在实数m，使得y=f（x）的图象与y=g（x）的图象有且只有两个不同的交点？若存在，求出m的值；若不存在，说明理由.
20、（本小题满分14分）（实验班学生做）
椭圆G：
的两个焦点F1（－c，0）、F2（c，0），M是椭圆上的一点，且满足
（Ⅰ）求离心率e的取值范围；
（Ⅱ）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为
求此时椭圆G的方程；（ⅱ）设斜率为k（k≠0）的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点
的直线对称？若能，求出k的取值范围；若不能，请说明理由
高三数学（理科）试卷答案
一、填空题
1、3 2、
;假 3、1 4、2 5、
6、
7、
8、
9、
10、
11、2 12、4 13、②④ 14、①
二、解答题
15解：（Ⅰ）设
的两根
则
…………………………………………2分
……………………………………4分
又
……………………………………………6分
（Ⅱ）由
①………………8分
由余弦定理：
即：
②………………………………………………10分
由①②得：a=8，b=5 …………………………………………12分
16、解证：（Ⅰ）
…………………………1分
当n≥2时，
…………2分
故是以2为首项，以2为公差的等差数列.……………………4分
（Ⅱ）由（Ⅰ）得
……………5分
当n≥2时，
………………………6分
当n=1时，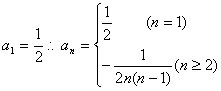
………………8分
（Ⅲ）1°当n=1时，
成立……………………9分
2°假设n=k时，不等式成立，即
成立
则当n=k+1时，
即当n=k+1时，不等式成立
由1°，2°可知对任意n∈N*不等式成立.
（Ⅲ）另证：
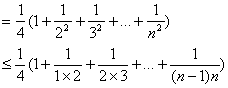
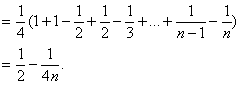
…………………………12分
17、解：（I）f（0）=10表示当甲公司不投入宣传费时，乙公司要避免新产品的开发有失败风险，至少要投入10万元宣传费；g（0）=20表示当乙公司不投入宣传费时，甲公司要避免新产品的开发有失败的风险，至少要投入20万元宣传费。………………………………4分
（Ⅱ）设甲公司投入宣传费x万元，乙公司投入宣传费y万元，依题意，当且仅当
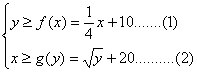成立，双方均无失败的风险……8分
由（1）（2）得
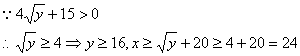
答：要使双方均无失败风险，甲公司至少要投入24万元，乙公司至少要投入16万元。
18、（本小题满分12分）
解：(I)由，得
．……………………………………2分
当x=1时，切线l的斜率为3，可得2a+b=0． ①
当时，有极值，则
，可得4a+3b+4=0．②
由①、②解得 a=2,b=-4．……………………………………5分
设切线l的方程为 
．
由原点到切线l的距离为，
则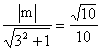
．解得m=±1．
∵切线l不过第四象限，
∴m=1．……………………………………6分
由于l切点的横坐标为x=1，∴
．
∴1+a+b+c=4．
∴c=5．…………………………………………………………………7分
(II)由(I)可得
，
∴
．……………………………………8分
令
，得x=－2, ．
| x | [-3,-2) | -2 | (-2, |
| ( |
|
| + | 0 | - | 0 | + |
| f(x) |
| 极大值 |
| 极小值 |
|
)
…………………………10分
∴f(x)在x=－2处取得极大值f(-2)=13．
在处取得极小值
=
．
又f(-3)=8，f(1)=4．
∴f(x)在[-3,1]上的最大值为13，最小值为．…………………12分
19（普通班学生做）（1）
，
，
猜想
（2）
，
（1）当
，即
时，函数
在区间上是减函数
当
时，
，即
，该方程没有整数解
（2）当
，即
时，
，解得
，综上所述，
20、（普通班学生做）解：（Ⅰ）由题意：抛物线焦点为（1，0）
设
消去x得
则
……………………………………4分
=
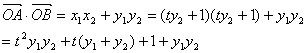
…………………………6分
（Ⅱ）法一：设
消去x，得
则y1+y2=4t y1y2=－4b………………………………8分
=
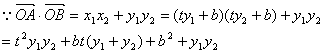
…………………………10分
令
∴直线l过定点（2，0）……………………………………12分
法二：设
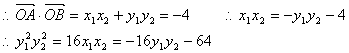
……8分
①当直线l的斜率不存在时，l⊥x轴x1=x2
∵
=4 ∴x1=x2=2
此时直线l过（2，0）点…………………………………………9分
②当直线l的斜率存在时
∴
∴
∴l的方程为：
即 
∴
此时直线l过定点（2，0）
综上，直线l过定点（2，0）. ……………………………………12分
19、（本小题满分14分）（实验班学生做）
解：（I）由图形 知：
，
∴函数f（x）的解析式为
…………………………4分
（Ⅱ）由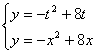
得
∵0≤t≤2
∴直线l1与f（x）的图象的交点坐标为（
………………6分
由定积分的几何意义知：
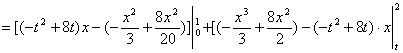
………………………………9分
（Ⅲ）令
因为x＞0，要使函数f（x）与函数g（x）有且仅有2个不同的交点，则函数
的图象与x轴的正半轴有且只有两个不同的交点
当x∈（0，1）时，
是增函数；
当x∈（1，3）时，
是减函数
当x∈（3，+∞）时，是增函数
当x=1或x=3时，
∴
…………………………12分
又因为当x→0时，
当
所以要使
有且仅有两个不同的正根，必须且只须
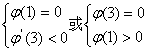
即
∴m=7或
∴当m=7或时，函数f（x）与g（x）的图象有且只有两个不同交点。
20（实验班学生做）
解：（I）设M（x0，y0）
①
又
②……………2分
由②得
代入①式整理得 
又
解得
…………………………………………………………4分
（Ⅱ）（i）当
设H（x，y）为椭圆上一点，则
若0
由
（舍去）………………………6分
若b≥3，当y=－3时，HN2有最大值2b2+18
由2b2+18=50得b2=16
∴所求椭圆方程为
……………………………………8分
（ii）设A（x1，y1），B（x2，y2），Q（x0，y0），则由
③
又直线PQ⊥直线l ∴直线PQ方程为
将点Q（x0，y0）代入上式得，
④………11分
由③④得Q
…………………………………………12分
（解1）而Q点必在椭圆内部 
由此得
故当
时A、B两点关于点P、Q的直线对（14分）
（解2）∴AB所在直线方程为
由
得
显然1+2k2≠0
而
直线l与椭圆有两不同的交点A、B ∴△＞0
解得
故当时，A、B两点关于点P、Q的直线对称。…………………………………………………………14分
（ii）另解；设直线l的方程为y=kx+b
由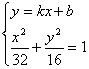
得
设A（x1，y1），B（x2，y2），Q（x0，y0），则
③……9分
又直线PQ⊥直线l ∴直线PQ方程为
将点Q（x0，y0）代入上式得， ④……10分
将③代入④
⑤………………………………11分
∵x1，x2是（*）的两根
⑥……12分
⑤代入⑥得
∴当时，A、B两点关于点P、Q的直线对称。………………………………………………………14分