08年普通高等学校招生全国考试理科数学四川延考卷
一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)集合![]() ,
,![]() 的子集中,含有元素
的子集中,含有元素![]() 的子集共有
的子集共有
(A)2个 (B)4个 (C)6个 (D)8个
解:![]() 的子集共
的子集共![]() 个,含有元素0的和不含元素0的子集各占一半,有4个.选B
个,含有元素0的和不含元素0的子集各占一半,有4个.选B
(2)已知复数![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:![]()
![]()
(3)![]() 的展开式中含
的展开式中含![]() 的项的系数为
的项的系数为
(A)4 (B)6 (C)10 (D)12
解:![]() 展开式中含
展开式中含![]() 项的系数为
项的系数为![]()
(4)已知![]() ,则不等式
,则不等式![]() 的解集为
的解集为
(A)![]() ≥199,
≥199,![]() (B)
(B)![]() ≥200,
≥200,![]()
(C)![]() ≥201,
≥201,![]() (D)
(D)![]() ≥202,
≥202,![]()
解:![]()
![]()
(5)已知![]() ,则
,则![]() (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解: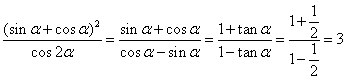 ,选C
,选C
(6)一个正三棱锥的底面边长等于一个球的半径,该正三棱锥的高等于这个球的直径,则球的体积与正三棱锥体积的比值为(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解: 设球的半径为![]()
![]() ;正三棱锥的底面面积
;正三棱锥的底面面积![]() ,
,![]() ,
,
![]() 。所以
。所以 ![]() ,选A
,选A
(7)若点![]() 到双曲线
到双曲线![]() 的一条淅近线的距离为
的一条淅近线的距离为![]() ,则双曲线的离心率为
,则双曲线的离心率为
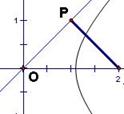 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:设过一象限的渐近线倾斜角为![]()
![]()
所以![]()
![]() ,因此
,因此![]() ,选A。
,选A。
(8)在一次读书活动中,一同学从4本不同的科技书和2本不同的文艺书中任选3本,则所选的书中既有科技书又有文艺书的概率为(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:因文艺书只有2本,所以选3本必有科技书。问题等价于选3本书有文艺书的概率:
![]()
(9)过点![]() 的直线与圆
的直线与圆![]() 相交于
相交于![]() 两点,则
两点,则![]() 的最小值为
的最小值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解: 弦心距最大为![]() ,
,![]() 的最小值为
的最小值为![]()
(10)已知两个单位向量![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() 的充要条件是
的充要条件是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解:![]()
![]() ,选C
,选C
(11)设函数![]()
![]() 的图象关于直线
的图象关于直线![]() 及直线
及直线![]() 对称,且
对称,且![]() 时,
时,![]() ,则
,则![]() (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:![]()
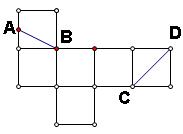 (12)一个正方体的展开图如图所示,
(12)一个正方体的展开图如图所示,![]() 为原正方体的顶点,
为原正方体的顶点,![]() 为原正方体一条棱的中点。在原来的正方体中,
为原正方体一条棱的中点。在原来的正方体中,![]() 与
与![]() 所成角的余弦值为 (A)
所成角的余弦值为 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
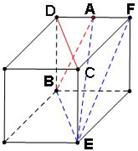 解:还原正方体如右图所示设
解:还原正方体如右图所示设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,
,![]() 与
与![]() 所成角等于
所成角等于![]() 与
与![]() 所成角,
所成角,
所以余弦值为![]() ,选 D
,选 D
二.填空题:本大题共4小题,每小题4分,共16分。把答案填在题中模式横线上。
(13)函数![]()
![]() 的反函数为 。
的反函数为 。
解:![]() ,所以反函数
,所以反函数![]() ,
,
(14)设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。若
。若![]() ,则
,则![]() 。
。
解:![]() ,取特殊值
,取特殊值
令![]()
![]()
![]() ,所以
,所以![]()
(15)已知函数![]()
![]() 在
在![]() 单调增加,在
单调增加,在![]() 单调减少,则
单调减少,则![]() 。
。
解:由题意![]()
![]()
又![]() ,令
,令![]() 得
得![]() 。(如
。(如![]() ,则
,则![]() ,
,![]() 与已知矛盾)
与已知矛盾)
(16)已知![]() ,
,![]() 为空间中一点,且
为空间中一点,且![]() ,则直线
,则直线![]() 与平面
与平面![]()
所成角的正弦值为 。
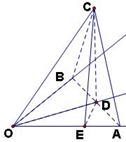 解:由对称性点
解:由对称性点![]() 在平面
在平面![]() 内的射影
内的射影![]() 必在
必在![]() 的平分线上作
的平分线上作![]() 于
于![]() ,连结
,连结![]() 则由三垂线定理
则由三垂线定理![]() ,
,
设![]()
![]() ,又
,又![]() ,所以
,所以![]() ,因此直线
,因此直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]()
三.解答题:本大题共6个小题,共74分。解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)在△![]() 中,内角
中,内角![]() 对边的边长分别是
对边的边长分别是![]() ,已知
,已知![]() 。
。
(Ⅰ)若![]() ,且
,且![]() 为钝角,求内角
为钝角,求内角![]() 与
与![]() 的大小;
的大小;
(Ⅱ)若![]() ,求△
,求△![]() 面积的最大值。
面积的最大值。
解:(Ⅰ)由题设及正弦定理,有![]() 。
。
故![]() 。因
。因![]() 为钝角,所以
为钝角,所以![]() 。
。
由![]() ,可得
,可得![]() ,得
,得![]() ,
,![]() 。
。
(Ⅱ)由余弦定理及条件![]() ,有
,有![]() ,故
,故![]() ≥
≥![]() 。
。
由于△![]() 面积
面积![]() ,
,
又![]() ≤
≤![]() ,
,![]() ≤
≤![]() ,
,
当![]() 时,两个不等式中等号同时成立,
时,两个不等式中等号同时成立,
所以△![]() 面积的最大值为
面积的最大值为![]() 。
。
(18)(本小题满分12分)一条生产线上生产的产品按质量情况分为三类:![]() 类、
类、![]() 类、
类、![]() 类。检验员定时从该生产线上任取2件产品进行一次抽检,若发现其中含有
类。检验员定时从该生产线上任取2件产品进行一次抽检,若发现其中含有![]() 类产品或2件都是
类产品或2件都是![]() 类产品,就需要调整设备,否则不需要调整。已知该生产线上生产的每件产品为
类产品,就需要调整设备,否则不需要调整。已知该生产线上生产的每件产品为![]() 类品,
类品,![]() 类品和
类品和![]() 类品的概率分别为
类品的概率分别为![]() ,
,![]() 和
和![]() ,且各件产品的质量情况互不影响。
,且各件产品的质量情况互不影响。
(Ⅰ)求在一次抽检后,设备不需要调整的概率;
(Ⅱ)若检验员一天抽检3次,以![]() 表示一天中需要调整设备的次数,求
表示一天中需要调整设备的次数,求![]() 的分布列和数学期望。
的分布列和数学期望。
解:(Ⅰ)设![]() 表示事件“在一次抽检中抽到的第
表示事件“在一次抽检中抽到的第![]() 件产品为
件产品为![]() 类品”,
类品”,![]()
![]() 表示事件“在一次抽检中抽到的第
表示事件“在一次抽检中抽到的第![]() 件产品为
件产品为![]() 类品”,
类品”,![]()
![]() 表示事件“一次抽检后,设备不需要调整”。
表示事件“一次抽检后,设备不需要调整”。
则![]() 。
。
由已知![]() ,
,![]()
![]()
所以,所求的概率为![]()
![]() 。
。
(Ⅱ)由(Ⅰ)知一次抽检后,设备需要调整的概率为
![]() ,依题意知
,依题意知![]() ,
,![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
|
| 0.729 | 0.243 | 0.027 | 0.001 |
![]() 。
。
(19)(本小题满分12分)
如图,一张平行四边形的硬纸片![]() 中,
中,![]() ,
,![]() 。沿它的对角线
。沿它的对角线![]() 把
把
△![]() 折起,使点
折起,使点![]() 到达平面
到达平面![]() 外点
外点![]() 的位置。
的位置。
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)如果△![]() 为等腰三角形,求二面角
为等腰三角形,求二面角![]() 的大小。
的大小。
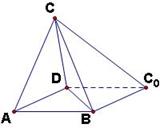 解:(Ⅰ)证明:因为
解:(Ⅰ)证明:因为![]()
![]() ,
,![]() ,
,
所以![]() ,
,![]() 。
。
因为折叠过程中,![]() ,
,
所以![]() ,又
,又![]() ,故
,故![]() 平面
平面![]() 。
。
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() 。
。
(Ⅱ)解法一:如图,延长![]() 到
到![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() 。
。
因为![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() 为正方形,
为正方形,![]() 。
。
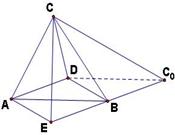 由于
由于![]() ,
,![]() 都与平面
都与平面![]() 垂直,所以
垂直,所以![]() ,可知
,可知![]() 。
。
因此只有![]() 时,△
时,△![]() 为等腰三角形。
为等腰三角形。
在![]() △
△![]() 中,
中,![]() ,又
,又![]() ,
,
所以△![]() 为等边三角形,
为等边三角形,![]() 。
。
由(Ⅰ)可知,,所以![]() 为二面角
为二面角![]() 的平面角,即二面角
的平面角,即二面角![]() 的大小为
的大小为![]() 。
。
解法二:以![]() 为坐标原点,射线
为坐标原点,射线![]() ,
,![]() 分别为
分别为![]() 轴正半轴和
轴正半轴和![]() 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() 。
。
由(Ⅰ)可设点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() ,则有
,则有![]() 。 ①
。 ①
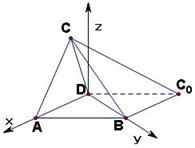 因为△
因为△![]() 为等腰三角形,所以
为等腰三角形,所以![]() 或
或![]() 。
。
若![]() ,则有
,则有![]() 。
。
则此得![]() ,
,![]() ,不合题意。
,不合题意。
若![]() ,则有
,则有![]() 。
②
。
②
联立①和②得![]() ,
,![]() 。故点
。故点![]() 的坐标为
的坐标为![]() 。
。
由于![]() ,
,![]() ,所以
,所以![]() 与
与![]() 夹角的大小等于二面角
夹角的大小等于二面角![]() 的大小。
的大小。
又![]() ,
,![]() ,
,![]()
所以![]() 即二面角
即二面角![]() 的大小为
的大小为![]() 。
。
(20)(本小题满分12分)在数列![]() 中,
中,![]() ,
,![]() 。
。
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
(Ⅲ)求数列![]() 的前
的前![]() 项和
项和![]() 。
。
解:(Ⅰ)由条件得![]() ,又
,又![]() 时,
时,![]() ,
,
故数列![]() 构成首项为1,公式为
构成首项为1,公式为![]() 的等比数列.从而
的等比数列.从而![]() ,即
,即![]() .
.
(Ⅱ)由![]() 得
得![]() ,
,
![]() ,
,
两式相减得 : ![]() , 所以
, 所以 ![]() .
.
(Ⅲ)由![]() 得
得
![]()
所以![]()
![]() .
.
(21)(本小题满分12分)
已知椭圆![]() 的中心和抛物线
的中心和抛物线![]() 的顶点都在坐标原点
的顶点都在坐标原点![]() ,
,![]() 和
和![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 的长轴长、短轴长及点
的长轴长、短轴长及点![]() 到
到![]() 右准线的距离成等比数列。
右准线的距离成等比数列。
(Ⅰ)当![]() 的准线与
的准线与![]() 右准线间的距离为
右准线间的距离为![]() 时,求
时,求![]() 及
及![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 于
于![]() ,
,![]() 两点。当
两点。当![]() 时,求
时,求![]() 的值。
的值。
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由(Ⅰ)知![]() ,即
,即![]()
由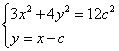 , 知
, 知![]() 满足
满足 ![]() ,
,
从而![]()
由条件![]() ,得
,得![]() , 故
, 故![]() :
:![]() .
.
由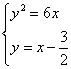 得
得![]() ,所以
,所以![]()
于是![]()
(22)(本小题满分14分)
设函数![]() 。
。
(Ⅰ)求![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对一切![]() ,
,![]() ,求
,求![]() 的最大值。
的最大值。
解:(Ⅰ)![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
故![]() 在
在![]() 单调增加,在
单调增加,在![]() 单调减少。
单调减少。
![]() 的极小值
的极小值![]() ,极大值
,极大值![]()
(Ⅱ)由![]() 知
知
![]() 即
即 ![]()
由此及(Ⅰ)知![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]()
因此对一切![]() ,
,![]() 的充要条件是,
的充要条件是,
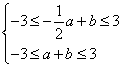
即![]() ,
,![]() 满足约束条件
满足约束条件
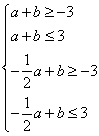 ,
,
由线性规划得,![]() 的最大值为5.
的最大值为5.