09届高三(文科)数学周周练(一)
命题人:袁春伟
2008-7-22
一、
|
1、已知集合![]() =
=![]() ,
,![]() ,则
,则![]() = ▲ __
= ▲ __
2、函数![]() 的单调增区间是
▲
的单调增区间是
▲
3、函数![]() 的定义域为
的定义域为![]() ,则
,则![]() 的定义域为___ ▲ __
的定义域为___ ▲ __
4、设函数![]() 是奇函数且周期为3,
是奇函数且周期为3,![]() = ▲
= ▲
5、若![]() 对任意的正实数x成立,则
对任意的正实数x成立,则![]()
![]()
![]() ▲
▲
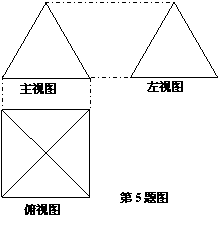 6、如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是 ▲
6、如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是 ▲
7、若椭圆![]() (0<m<1)的离心率为
(0<m<1)的离心率为![]() ,则它的长轴长为 ▲
,则它的长轴长为 ▲
8、若不等式1-![]() <0有解,则实数a的范围是
<0有解,则实数a的范围是
 9、若三条直线
9、若三条直线![]() 不能构成三角形,则m可取得的值构成的集合是
▲
不能构成三角形,则m可取得的值构成的集合是
▲
10、圆![]() 上一点到直线
上一点到直线![]() 的距离的最小值为 ▲
的距离的最小值为 ▲
11、给出下列关于互不相同的直线![]() 和平面
和平面![]() 的四个命题:
的四个命题:
(1)![]() 则
则![]() 与m不共面;
与m不共面;
(2)![]() 、m是异面直线,
、m是异面直线,![]() ;
;
(3)若![]() ,则
,则![]()
 (4)若
(4)若![]() 其中真命题是 ▲ (填序号)
其中真命题是 ▲ (填序号)
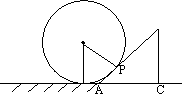
12、水平地面上有一个球,现用如下方法测量球的表面积,用锐角![]() 的等腰直角三角板的斜边紧靠球面,P为切点,一条直角边AC紧靠地面,并使三角板与地面垂直,如果测得PA=1m,则球的表面积等于 ▲
的等腰直角三角板的斜边紧靠球面,P为切点,一条直角边AC紧靠地面,并使三角板与地面垂直,如果测得PA=1m,则球的表面积等于 ▲
13、函数![]() 在
在![]() 上的单调递增区间为 ▲
上的单调递增区间为 ▲
14、已知(![]() ,
,![]() )是直线
)是直线![]() 与圆
与圆![]() 的交点,则
的交点,则![]() 的取值范围为 ▲
的取值范围为 ▲
二、解答题: 本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤
15、(本题满分14分)直线![]() 经过点A(2,4),且被平行直线x-y+1=0与x-y-1=0所截得的线段的中点在直线x+y-3=0上,求直线
经过点A(2,4),且被平行直线x-y+1=0与x-y-1=0所截得的线段的中点在直线x+y-3=0上,求直线![]() 的方程
的方程
 16、(本题满分14分)已知集合A={xx2-2x-8≤0,x∈R},B={xx2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
16、(本题满分14分)已知集合A={xx2-2x-8≤0,x∈R},B={xx2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若AÌ∁RB,求实数m的取值范围.
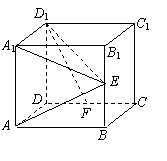
17、(本题满分15分)在正方体ABCD-A1B1C1D1中,
E、F分别是BB1、CD的中点.
(1)求证AE⊥D1F;
(2)证明平面AED⊥平面A1FD1.
18、(本题满分15分)已知过点A(0,1),且方向向量为![]() ,相交于M、N两点.
,相交于M、N两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() ;
;
(3)若O为坐标原点,且![]()
19、(本题满分16分)已知直线![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到点
上的点到点![]() 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆![]() 的标准方程;(7分)
的标准方程;(7分)
(Ⅱ)已知圆![]() ,直线
,直线![]() .试证明当点
.试证明当点![]() 在椭圆
在椭圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 恒相交;并求直线
恒相交;并求直线![]() 被圆
被圆![]() 所截得的弦长的取值范围.
所截得的弦长的取值范围.
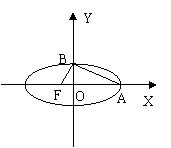
20、(本题满分16分)圆![]() 与x轴交于F1、F2两点,P为圆上一点.椭圆
与x轴交于F1、F2两点,P为圆上一点.椭圆![]() 以F1、F2为焦点且过点P.
以F1、F2为焦点且过点P.
(Ⅰ)当P点坐标为![]() 时,求x0的值及椭圆方程;
时,求x0的值及椭圆方程;
(Ⅱ)当P点在圆上运动时(不与F1、F2重合),求椭圆离心率e的取值范围;
高三(文科)数学周周练(一)答案:
1、![]() 2、
2、![]() 3、
3、![]() 4、1 5、2009 6、
4、1 5、2009 6、![]() 7、4
8、(0,1)
7、4
8、(0,1)![]()
9、{-3,-1,2} 10、2 11、(1)、(2)、(3)12、(12+![]() 13、
13、![]() 14、
14、![]()
15、解:中点在x+y-3=0上,同时它在到两平行直线距离相等的直线x-y=0上,从而求得中点坐标为(![]() ,
,![]() ),由直线
),由直线![]() 过点(2,4)和点(
过点(2,4)和点(![]() ,
,![]() ),得直线
),得直线![]() 的方程为5x-y-6=0
的方程为5x-y-6=0
16、由已知得A=[-2,4],B=[m-3,m].
(1)∵A∩B=[2,4],∴∴m=5.
(2)∵B=[m-3,m],∴∁RB=(-∞,m-3)∪(m,+∞).
∵AÌ∁RB,∴m-3>4或m<-2.∴m>7或m<-2.∴m∈(-∞,-2)∪(7,+∞).
17、(1)取AB的中点G,则易证得A1G∥D1F.又正方形A1ABB1中,E、G分别是相应边的中点,
∴A1G⊥AE,∴D1F⊥AE.
(2)由正方体可知:A1 D1⊥面A1ABB1,∴A1D1⊥AE .又由(1)已证:D1F⊥AE.
∵A1D1∩D1F= D1,∴AE⊥平面A1FD1 .又![]() 平面AED, ∴平面AED⊥平面A1FD1 .
平面AED, ∴平面AED⊥平面A1FD1 .
18、解:(1)![]()
![]()
由![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
19、解: (Ⅰ)由![]() ,得
,得![]() ,
,
则由![]() ,解得F(3,0). 设椭圆
,解得F(3,0). 设椭圆![]() 的方程为
的方程为![]() ,则
,则
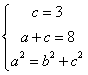 ,解得
,解得![]() 所以椭圆
所以椭圆![]() 的方程为
的方程为![]()
(Ⅱ)因为点![]() 在椭圆
在椭圆![]() 上运动,所以
上运动,所以![]() , 从而圆心
, 从而圆心![]() 到直线
到直线![]() 的距离
的距离![]() . 所以直线
. 所以直线![]() 与圆
与圆![]() 恒相交
恒相交
又直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]()
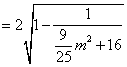
由于![]() ,所以
,所以![]() ,则
,则![]() ,
,
即直线![]() 被圆
被圆![]() 截得的弦长的取值范围是
截得的弦长的取值范围是![]()
20、解:(Ⅰ)由圆与x轴的交点为![]() 得椭圆的焦距2c=2
得椭圆的焦距2c=2![]()
∴![]() ∴椭圆的方程可化为
∴椭圆的方程可化为![]() ①
①
将![]() 代入圆得
代入圆得 ![]() ∴
∴![]() ,
,
∴![]() 代入①式得
代入①式得 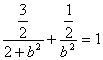
∴b2=1 ∴所求椭圆的方程为 ![]()
(Ⅱ)设![]() ∵P是圆上点 ∴有
∵P是圆上点 ∴有![]() ②
②
由r1+r2=2a 得![]() ③
③
由②③得 ![]() ∵
∵![]() 当且仅当r1=r2时等号成立
当且仅当r1=r2时等号成立
∴有![]() ∴
∴![]()
由e<1 ∴椭圆的离心率e的取值范围是 ![]()