09届高三数学(文科)周考三
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合![]() ,
,![]() ,
,![]() ,则
,则![]() =( D
)
=( D
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若命题p:x∈A∪B,则![]() p是( A
)
p是( A
)
A.x ![]() A且x
A且x ![]() B B.x
B B.x ![]() A或x
A或x ![]() B C.
B C.![]() D.
D.![]()
3.若![]() ,
,![]() , 则
, 则![]() ( B
)
( B
)
A.(1,1) B.(-1,-1) C.(3,7) D.(-3,-7)
4.已知平面向量![]() ,
,![]() ,且
,且![]() //
//![]() ,则
,则![]() =( C )
=( C )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、已知平面向量![]() =(1,-3),
=(1,-3),![]() =(4,-2),
=(4,-2),![]() 与
与![]() 垂直,则
垂直,则![]() 是( D
)
是( D
)
A. 2 B. 1 C. -2 D. -1
6、平面向量![]() ,
,![]() 共线的充要条件是( B )
共线的充要条件是( B )
A. ![]() ,
, ![]() B.
存在不全为零的实数
B.
存在不全为零的实数![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() 方向相同 D.
方向相同 D. ![]() ,
,![]() 两向量中至少有一个为零向量
两向量中至少有一个为零向量
7.“若一个数不是负数,则它的平方不是正数.”和这个命题真值相同的命题为 ( C )
A.“若一个数是负数,则它的平方是正数.”
B.“若一个数的平方不是正数,则它不是负数.”
C.“若一个数的平方是正数,则它是负数.”
D.“若一个数不是负数,则它的平方是非负数.”
8. 命题“若函数![]() 在其定义域内是减函数,则
在其定义域内是减函数,则![]() ”的逆否命题是( A )
”的逆否命题是( A )
A、若![]() ,则函数
,则函数![]() 在其定义域内不是减函数
在其定义域内不是减函数
B、若![]() ,则函数
,则函数![]() 在其定义域内不是减函数
在其定义域内不是减函数
C、若![]() ,则函数
,则函数![]() 在其定义域内是减函数
在其定义域内是减函数
D、若![]() ,则函数
,则函数![]() 在其定义域内是减函数
在其定义域内是减函数
9.在![]() 中,
中,![]() ,
,![]() .若点
.若点![]() 满足
满足![]() ,则
,则![]() =( B
)
=( B
)
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、函数![]() 的最小值和最大值分别为( B
)
的最小值和最大值分别为( B
)
A. -3,1
B. -3,![]() C. -2,2 D. -2,
C. -2,2 D. -2,![]()
11.给出下列三个命题 :
①若![]() ,则
,则![]() ;
;
②若正整数m和n满足![]() ,则
,则![]() ;
;
③设![]() 为圆
为圆![]() 上任一点,圆
上任一点,圆![]() 以
以![]() 为圆心且半径为1.当
为圆心且半径为1.当![]() 时,圆
时,圆![]() 与圆
与圆![]() 相切;其中假命题的个数为( B )
相切;其中假命题的个数为( B )
A.0 B.1 C.2 D.3
12.计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:E+D=1B,则A×B=( A )
A.6E B.B0 C.5F D.72
二、填空题(本大题共4小题,每小题4分,共16分把答案填在题中横线上)
13.设向量![]() ,若向量
,若向量![]() 与向量
与向量![]() 共线,则
共线,则![]() .2
.2
14.已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,那么
,那么![]() 的值为________.
的值为________.![]()
15.已知集合![]() ,
,![]() ,则
,则![]() =
;
=
;![]()
16.如图,正六边形![]() 中,有下列四个命题:
中,有下列四个命题:
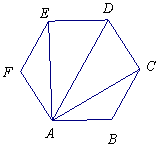 A.
A.![]()
B.![]()
C.![]()
D.![]()
其中真命题的代号是
(写出所有真命题的代号).![]()
三、解答题(共6小题,共74分)
17.(本小题满分12分)
已知ΔABC三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(![]() ,0).
,0).
(1)若![]() ,求
,求![]() 的值;(2)若
的值;(2)若![]() ,求sinA的值。
,求sinA的值。
17.解: (1) ![]()
![]()
由 ![]() 得
得 ![]() ……6分
……6分
(2)![]()
![]()
![]() ……12分
……12分
18.(本小题满分12分)
已知向量a=(sinθ,1),b=(1,cosθ),- <θ<。
(1)若a⊥b,求θ; (2)求|a+b|的最大值.
18.解:(1)若a⊥b,则sinθ+cosθ=0,…3分
由此得 tanθ=-1(-<θ<=,所以 θ=-;…6分
(2)由a=(sinθ,1),b=(1,cosθ)得|a+b|===,…10分 当sin(θ+)=1时,a+b取得最大值,即当θ=时,a+b最大值为+1.…12分
19.(本小题满分12分)
已知函数![]()
(1)求函数![]() 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(2)求函数![]() 在区间
在区间![]() 上的值域
上的值域
解:(1)![]()
![]()
![]()
![]()
![]()
![]() ……4分
……4分
令![]() 得
得![]() 的对称轴方程为
的对称轴方程为![]() ……6分
……6分
(2)![]() 因为
因为![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,所以 当
上单调递减,所以 当![]() 时,
时,![]() 取最大值 1又
取最大值 1又 ![]() ,
,![]() 当
当![]() 时,
时,![]() 取最小值
取最小值![]()
所以 函数 ![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ……12分
……12分
20.(本小题满分12分)
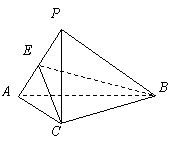
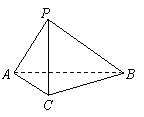 如图,在三棱锥
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
解法一:
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,![]() .
.
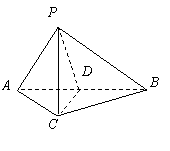
![]() ,
,![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .……6分
.……6分
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
 又
又![]() ,
,![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.![]() 二面角
二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .……12分
.……12分
21.(本小题满分12分)
等差数列{![]() }的前n项和记为Sn.已知
}的前n项和记为Sn.已知![]()
(1)求通项![]() ; (2)若Sn=242,求n.
; (2)若Sn=242,求n.
21.解:(1)由![]() 得方程组
得方程组
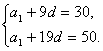 ……4分 解得
……4分 解得![]() 所以
所以 ![]() ……6分
……6分
(2)由![]() 得方程
得方程
![]() ……10分
解得
……10分
解得![]() ………12分
………12分
22.(本小题满分14分)
已知函数![]() 的图像与函数
的图像与函数![]() 的图象相切,记
的图象相切,记![]()
(1)求实数b的值及函数F(x)的极值;
(2)若关于x的方程F(x)=k恰有三个不等的实数根,求实数k的取值范围.
22.解:(1)依题意,令![]() ,得
,得![]()

列表如下:
|
|
|
|
| -1 |
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值0 | ↗ |
从上表可知![]() 处取得极小值. ………7分
处取得极小值. ………7分
(2)由(1)可知函数![]() 作函数
作函数![]() 的图象,当
的图象,当![]() 的图象与函数
的图象与函数![]() 的图象有三个交点时,关于x的方程
的图象有三个交点时,关于x的方程![]()
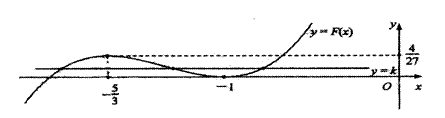
![]() ………14分
………14分