求指数、对数函数的导数
例 求下列函数的导数：
1．
；2．
；
3．
； 4．
分析：对于比较复杂的函数求导，除了利用指数、对数函数求导公式之外，还需要考虑应用复合函数的求导法则来进行．求导过程中，可以先适当进行变形化简，将对数函数的真数位置转化为有理函数的形式后再求导数．
解：1．解法一：可看成
复合而成．
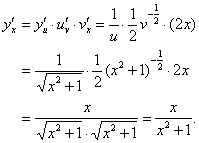
解法二：
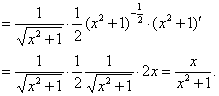
解法三：
，
2．解法一：设
，则
解法二：
3．解法一：设
，则
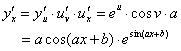
解法二：
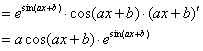
4．
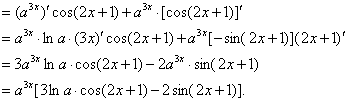
说明：深刻理解，掌握指数函数和对数函数的求导公式的结构规律，是解决问题的关键，解答本题所使用的知识，方法都是最基本的，但解法的构思是灵魂，有了它才能运用知识为解题服务，在求导过程中，学生易犯漏掉符合或混淆系数的错误，使解题走入困境．
解题时，能认真观察函数的结构特征，积极地进行联想化归，才能抓住问题的本质，把解题思路放开．
变形函数解析式求导
例 求下列函数的导数：
（1）
； （2）
；
（3）
； （4）
．
分析：先将函数适当变形，化为更易于求导的形式，可减少计算量．
解：（1）
．
（2）
，
（3）
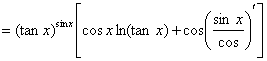
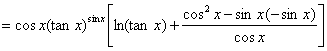
（4）
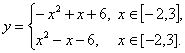
当
时
不存在．
说明：求
（其中
为多项式）的导数时，若
的次数不小于
的次数，则由多项式除法可知，存在
，使
．从而
，这里均为多项式，且
的次数小于的次数．再求导可减少计算量．
对函数变形要注意定义域．如
，则定义域变为
，所以虽然
的导数
与
的导数
结果相同，但我们还是应避免这种解法．
函数求导法则的综合运用
例 求下列函数的导数：
1．
；2．
；
3．
；4．
分析：式中所给函数是几个因式积、商、幂、开方的关系．对于这种结构形式的函数，可通过两边取对数后再求导，就可以使问题简单化或使无法求导的问题得以解决．但必须注意取寻数时需要满足的条件是真数为正实数，否则将会出现运算失误．
解：1．取y的绝对值，得
，两边取寻数，得
根据导数的运算法则及复合函数的求导法则，两端对x求导，得
，
∴
2．注意到
，两端取对数，得
∴
∴
3．两端取对数，得
，
两端对x求导，得
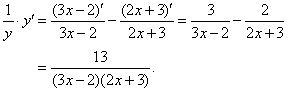
4．两端取对数，得
，
两边对x求导，得
∴
说明：对数求导法则实质上是复合函数求导法则的应用．从多角度分析和探索解决问题的途径，能运用恰当合理的思维视力，把问题的隐含挖掘出来加以利用，会使问题的解答避繁就简，化难为易，收到出奇制胜的效果．解决这类问题常见的错误是不注意
是关于x的复合函数．
指对数函数的概念揭示了各自存在的条件、基本性质及其几何特征，恰当地引入对数求导的方法，从不同的侧面分析转化，往往可避免繁琐的推理与运算，使问题得以解决．