数列的通项以及用归纳法证明不等式
例 在1与2之间插入![]() 个正数
个正数![]() ,使这
,使这![]() 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入![]() 个正数
个正数![]() ,使这
,使这![]() 个数成等差数列.记
个数成等差数列.记![]() .求:
.求:
(1)求数列![]() 和
和![]() 的通项;
的通项;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
分析:本题考查等差数列,等比数列的知识,以及观察、分析、归纳的能力和数学归纳法.
解:(1)![]() 成等比数列,
成等比数列,
![]()
![]()
![]()
![]() 成等差数列,
成等差数列,
![]()
![]()
所以数列![]() 的通项
的通项![]() ,数列
,数列![]() 的通项
的通项![]()
(2)![]() 要比较
要比较![]() 与
与![]() 的大小,只需比较
的大小,只需比较![]() 的大小,也就是比较当
的大小,也就是比较当![]() 时,
时,![]() 与
与![]() 的大小.
的大小.
当![]() 时,
时,![]() ,知
,知![]()
经验证,![]() 时,均有
时,均有![]() 成立,猜想,当
成立,猜想,当![]() 时有
时有![]() 下面用数学归纳法证明:
下面用数学归纳法证明:
(ⅰ)![]() 时已证
时已证![]()
(ⅱ)假设![]() 时不等式成立,即
时不等式成立,即![]() ,好么
,好么![]()
![]() 故
故![]() .即
.即![]() 时不等式也成立.
时不等式也成立.
根据(ⅰ)和(ⅱ)当![]() 时,
时,![]() 成立,即
成立,即![]()
说明:开放题求解要注意观察题目的特点,可以先通过特殊数尝试可能的结果,然后总结归纳出一般规律,利用归纳法证明结论.
猜想数列通项、利用归纳法证明不等式
例 设数列![]() 满足
满足![]()
(1)当![]() 时,求
时,求![]() ,并由此猜想出
,并由此猜想出![]() 的一个通项公式;
的一个通项公式;
(2)当![]() 时,证明对所有的
时,证明对所有的![]() ,有(ⅰ)
,有(ⅰ)![]()
(ⅱ)![]()
分析:本小题主要考查数列和不等式等知识,考查猜想、归纳、推理以及分析问题和解决问题的能力.
解:(1)由![]() 得
得![]()
由![]() 得
得![]()
由![]() ,得
,得![]()
由此猜想![]() 的一个通项公式:
的一个通项公式:![]()
(2)(ⅰ)用数学归纳法证明:
①当![]() ,不等式成立.
,不等式成立.
②假设当![]() 时不等式成立,即
时不等式成立,即![]() ,那么,
,那么,![]() 也就是说,当
也就是说,当![]() 时,
时,![]()
根据①和②,对于所有![]() ,有
,有![]()
(ⅱ)由![]() 及(ⅰ),对
及(ⅰ),对![]() ,有
,有![]() ……
……
![]()
于是![]()
![]()
![]()
![]()
说明:证明不等式的题型多种多样,所以不等式证明是一个难点,在由n=k成立,推导n=k+1不等式也成立时,过去讲的证明不等式的方法再次都可以使用,如比较法、放缩法、分析法、反证法等,有时还要考证与原不等式的等价的命题.
数列与归纳法的综合题
例 设![]() 为常数,且
为常数,且![]()
(Ⅰ)证明对任意![]()
(Ⅱ)假设对任意![]() 有
有![]() ,求
,求![]() 的取值范围.
的取值范围.
分析: 本小题主要考查数列、等比数列的概念,考查数学归纳法,考考灵活运用数学知识分析问题和解决问题的能力.
证明:(Ⅰ)证法一:(1)当![]() 时,由已知
时,由已知![]() ,等式成立.
,等式成立.
(ⅱ)假设当![]() 等式成立,即
等式成立,即![]()
那么![]()
![]()
也就是说,当![]() 时,等式也成立.
时,等式也成立.
根据(ⅰ)和(ⅱ)可知
证法二:如果设![]()
用![]() 代入,可解出
代入,可解出![]()
所以![]() 是公比的-2,首项为
是公比的-2,首项为![]() 的等比数列.
的等比数列.
![]()
即![]()
(Ⅱ)解法一:由![]() 通项公式
通项公式
![]()
![]() ①
①
(ⅰ)当![]() 时,①式即为
时,①式即为![]()
即为![]() ②
②
②式对![]() 都成立,有
都成立,有![]()
(ⅱ)当![]() 时,
时,![]()
即为![]() ③
③
③式对![]() 都成立,有
都成立,有![]()
综上,①式对任意![]() 成立,有
成立,有![]()
故![]() 的取值范围为
的取值范围为![]()
解法二:如果![]() 成立,特别取
成立,特别取![]() 有
有![]()
![]()
因此 ![]()
下面证明当![]() 时,对任意
时,对任意![]() ,有
,有![]()
由![]() 通项公式
通项公式
![]() ,时
,时
![]()
(2)当![]() 时,
时,
![]()
故![]() 的取值范围为
的取值范围为![]()
判断证明过程的正误
例 试判断下面的证明过程是否正确:
用数学归纳法证明:
![]()
证明:(1)当![]() 时,左边=1,右边=1
时,左边=1,右边=1
∴当![]() 时命题成立.
时命题成立.
(2)假设当![]() 时命题成立,即
时命题成立,即
![]()
则当![]() 时,需证
时,需证
![]()
由于左端等式是一个以1为首项,公差为3,项数为![]() 的等差数列的前
的等差数列的前![]() 项和,其和为
项和,其和为
![]()
∴![]() 式成立,即
式成立,即![]() 时,命题成立.根据(1)(2)可知,对一切
时,命题成立.根据(1)(2)可知,对一切![]() ,命题成立.
,命题成立.
分析:看一个用数学归纳法证明数学问题是否正确.关键要看两个步骤是否齐全,特别是第二步归纳假设是否被应用,如果没有用到归纳假设,那就是不正确的.
解: 以上用数学归纳法证明的过程是错误的.
在证明当![]() 时等式成立时,没有用到当
时等式成立时,没有用到当![]() 时命题成立的归纳假设,故不符合数学归纳法证题的要求.
时命题成立的归纳假设,故不符合数学归纳法证题的要求.
第二步正确的证明方法是:
假设当![]() 时命题成立,即
时命题成立,即
![]() 则当
则当![]() 时,
时,
![]()
![]()
即当![]() 时,命题成立.
时,命题成立.
说明:用数学归纳法证题的两个步骤相辅相成缺一不可.尽管有些与正整数有关的命题用其它方法也可以解决,但题目若要求用数学归纳法证明,则必须严格按照数学归纳法的步骤进行,否则是不正确的.
用数学归纳法证明等式
例 用数学归纳法证明
![]()
分析:用数学归纳法证明一个与整数有关的命题,关键是第二步,要注意当![]() 时,等式两边的式子与
时,等式两边的式子与![]() 时等式两边的式子的联系,增加了哪些项,减少了哪些项,问题就会顺利解决.
时等式两边的式子的联系,增加了哪些项,减少了哪些项,问题就会顺利解决.
证明:(1)当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,赞美式成立.
,赞美式成立.
(2)假设当![]() 时,等式成立,即
时,等式成立,即
![]() 则当
则当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
即当![]() 时,等式成立.
时,等式成立.
根据(1)、(2)可知,对一切![]() ,等式成立.
,等式成立.
说明:解题过程中容易将![]() 时,等式右边错写为
时,等式右边错写为![]() ,从而导致证明错误或无法进行.特别要注意等式右边的每一个式子都在随
,从而导致证明错误或无法进行.特别要注意等式右边的每一个式子都在随![]() 的变化而变化.
的变化而变化.
利用数学归纳法证明正切等式
例 用数学归纳法证明
![]() 分析:在由假设
分析:在由假设![]() 时等式成立,推导当
时等式成立,推导当![]() 时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:
时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:
![]() ,问题就会迎刃而解.
,问题就会迎刃而解.
证明:(1)当![]() 时,左边
时,左边![]()
右边![]() ,等式成立.
,等式成立.
(2)假设当![]() 时,
时,![]() 等式成立,即
等式成立,即
![]()
则当![]() 时,
时,
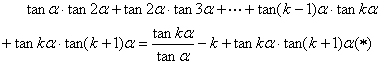
由![]() 得
得![]()
代入![]() 式,得
式,得
右边![]()
即![]()
![]()
这就是说,当![]() 时等式成立.
时等式成立.
根据(1)、(2)可知,对任意![]() ,等式成立.
,等式成立.
说明:灵活应用三角公式是解决三角问题常用的方法和技巧,恰当的应用公式是关键.如果应用公式![]() 来变形,本题就会出现困难.解决有关
来变形,本题就会出现困难.解决有关![]() 的式子时,经常要用到
的式子时,经常要用到![]() 展开式及其变形公式.
展开式及其变形公式.
利用归纳法证明整除问题
例 用数学归纳法证明:![]() 能被9整除.
能被9整除.![]() .
.
分析:证明一个与![]() 有关的式子
有关的式子![]() 能被一个数
能被一个数![]() (或一个代数式
(或一个代数式![]() )整除,主要是找到
)整除,主要是找到![]() 与
与![]() 的关系,设法找到式子
的关系,设法找到式子![]() ,使得
,使得![]() ,就可证昨命题成立.
,就可证昨命题成立.
证明:(1)当![]() 时,
时,![]() ,能被9整除,命题成立.
,能被9整除,命题成立.
(2)假设当![]() 时,
时,![]() 能被9整除,当
能被9整除,当![]() 时,
时,
![]()
![]()
![]() 和
和![]() 都能被9整除.
都能被9整除.
![]() 都能被9整除.
都能被9整除.
即![]() 能被9整除.
能被9整除.
即当![]() 时,命题成立.
时,命题成立.
由(1)、(2)可知,对任何![]() 命题都成立.
命题都成立.
说明:如果将![]() 时,
时,![]() 变为
变为![]() 能被9整除,困难就大一些.本题也可用二项式定理把
能被9整除,困难就大一些.本题也可用二项式定理把![]() 写成
写成![]() 展开后,再证明.
展开后,再证明.
用归纳法证明直线分割平面问题
例 平面内有![]() 条直线,其中任何两条不平行,任何三条不过同一点,证明这
条直线,其中任何两条不平行,任何三条不过同一点,证明这![]() 条直线把平面分成
条直线把平面分成![]() 个部分.
个部分.
分析:用数学归纳法证明几何问题,主要搞清楚当![]() 时比当
时比当![]() 时,分点增加了多少个,区城增加了多少块,线段增加了多少条.本问题中第
时,分点增加了多少个,区城增加了多少块,线段增加了多少条.本问题中第![]() 条直线与前
条直线与前![]() 条直线有
条直线有![]() 个分点,平面区域增加了
个分点,平面区域增加了![]() 块.
块.
证明:(1)当![]() 时,平面被分成2部分.
时,平面被分成2部分.
又![]() ,命题成立.
,命题成立.
(2)假设当![]() 时命题成立.即符合条件的
时命题成立.即符合条件的![]() 条直线把平面分成
条直线把平面分成![]() 个部分.现在来考虑平面内有
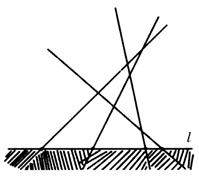
个部分.现在来考虑平面内有![]() 条直线的情况.任取其中的一条直线,记为
条直线的情况.任取其中的一条直线,记为![]() (如下图)图
(如下图)图![]() 与其它
与其它![]() 条直线有
条直线有![]() 个交点,平面区域增加了
个交点,平面区域增加了![]() 块,从而这
块,从而这![]() 条直线把平面分成了
条直线把平面分成了
![]()
![]()
![]()
根据(1)、(2)可知,命题对任何正整数都成立.
说明:不能错误地认为第![]() 条直线被其它
条直线被其它![]() 条直线分成
条直线分成![]() 段,区域增加了
段,区域增加了![]() 部分或2
部分或2![]() 部分.
部分.
证明有关几何问题,哪![]() 边形内角和公式,
边形内角和公式,![]() 边形对角线条数公式,还要确定初始值
边形对角线条数公式,还要确定初始值![]() 应为多少.由
应为多少.由![]() 到
到![]() 时又是如何变化的.
时又是如何变化的.
猜想并证明数列的通项
例 对于数列![]() ,若
,若![]()
(1)求![]() ,并猜想
,并猜想![]() 的表达式;
的表达式;
(2)用数学归纳法证明你的猜想.
分析:由已知条件,可直接求出![]() 式,通过观察归纳,猜想出
式,通过观察归纳,猜想出![]() 的表达式,再用数学归纳法加以证明.
的表达式,再用数学归纳法加以证明.
解:(1)![]()
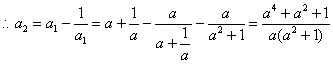
![]()
同理可得
![]()
猜想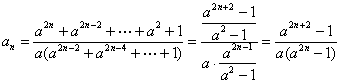
(2)(ⅰ)当![]() 时,右边
时,右边![]() ,等式成立.
,等式成立.
(ⅱ)假设当![]() 时
时![]() ,等式成立,即
,等式成立,即
![]() ,则当
,则当![]() 时,
时,
![]()
![]()
![]()
这就是说,当![]() 时,等式也成立.
时,等式也成立.
根据(ⅰ)、(ⅱ)可知,对于一切![]() ,
,![]() 成立.
成立.
说明:这类题型是常见题型,尤其是用数学归纳法证明与递推关系有关系的命题时,依归纳假设证明当![]() 时命题也成立时,除了用上假设之外,一定还得用上递推关系,否则假设也没法用.这是用数学归纳法证明递推关系时值得注意的地方.
时命题也成立时,除了用上假设之外,一定还得用上递推关系,否则假设也没法用.这是用数学归纳法证明递推关系时值得注意的地方.