2.3 直线、平面垂直的判定及其性质
一、选择题
1、“直线![]() 垂直于平面a内的无数条直线”是“
垂直于平面a内的无数条直线”是“![]() ⊥a”的
( )
⊥a”的
( )
A、充分条件B、必要条件C、充要条件D、既不充分也不必要条件
2、如果一条直线![]() 与平面a的一条垂线垂直,那么直线
与平面a的一条垂线垂直,那么直线![]() 与平面a的位置关系是 ( )
与平面a的位置关系是 ( )
A、![]() Ìa B、
Ìa B、![]() ⊥a C、
⊥a C、![]() ∥a D、
∥a D、![]() Ìa或
Ìa或![]() ∥a
∥a
3、若两直线a⊥b,且a⊥平面a,则b与a的位置关系是 ( )
A、相交 B、b∥a C、bÌa D、b∥a,或bÌa
4、a∥![]() ,则a平行于
,则a平行于![]() 内的( )
内的( )
A、一条确定的直线 B、任意一条直线
C、所有直线 D、无数多条平行线
5、如果直线a∥平面![]() ,那么直线a与平面
,那么直线a与平面![]() 内的
( )
内的
( )
A、一条直线不相交 B、两条直线不相交
C、无数条直线不相交 D、任意一条直线都不相交
6、若直线l上有两点P、Q到平面![]() 的距离相等,则直线l与平面
的距离相等,则直线l与平面![]() 的位置关系是( )
的位置关系是( )
A、平行 B、相交
C、平行或相交
D、平行、相交或在平面![]() 内
内
二、填空题
7、过直线外一点作直线的垂线有 条;垂面有 个;平行线有 条;平行平面
有 个.
8、过平面外一点作该平面的垂线有 条;垂面有 个;平行线有 条;平行平面有 个.
9、过一点可作________个平面与已知平面垂直.
10、过平面α的一条斜线可作_________个平面与平面α垂直.
11、过平面α的一条平行线可作_________个平面与平面α垂直.
三、解答题
12、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面![]()
13、过一点和已知平面垂直的直线只有一条![]()
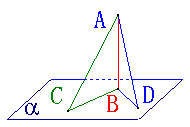
14、有一根旗杆![]() 高
高![]() ,它的顶端
,它的顶端![]() 挂一条长
挂一条长![]() 的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上)
的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上)![]() ,如果这两点都和旗杆脚
,如果这两点都和旗杆脚![]() 的距离是
的距离是![]() ,那么旗杆就和地面垂直,为什么?
,那么旗杆就和地面垂直,为什么?
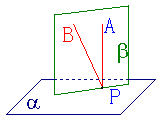
15、已知直线![]() ⊥平面α,垂足为A,直线AP⊥
⊥平面α,垂足为A,直线AP⊥![]()
![]()
求证:AP在α内![]()
参考答案
一、选择题
1、B;2、D;3、D;4、D;5、D;6、D
二、填空题
7、无数,一,一,无数
8、一,无数,无数,一
9、无数
10、一个
11、一个
三、解答题
12、已知:a∥b,a⊥![]()
求证:b⊥α![]()
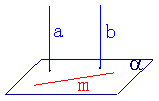 证明:设
证明:设![]() 是
是![]() 内的任意一条直线
内的任意一条直线![]()
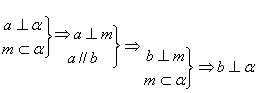
 13、已知:平面
13、已知:平面![]() 和一点P
和一点P![]()
求证:过点P与![]() 垂直的直线只有一条
垂直的直线只有一条![]()
证明:不论![]() 在平面
在平面![]() 内或外,设直线
内或外,设直线![]() ,垂足为
,垂足为![]() (或
(或![]() )
)
若另一直线![]() ,设
,设![]() 确定的平面为
确定的平面为![]() ,且
,且![]()
 ∴
∴![]()
又∵![]() 在平面
在平面![]() 内,与平面几何中的定理矛盾
内,与平面几何中的定理矛盾
所以过点![]() 与
与![]() 垂直的直线只有一条
垂直的直线只有一条![]()
14、解:在![]() 和
和![]() 中,
中,
 ∵
∵![]()
∴![]()
![]()
∴![]()
即![]()
又∵![]() 不共线
不共线
∴![]() 平面
平面![]() ,即旗杆和地面垂直;
,即旗杆和地面垂直;
15、证明:设AP与![]() 确定的平面为β
确定的平面为β![]() 如果AP不在α内,
如果AP不在α内,
则可设α与β相交于直线AM![]()
∵![]() ⊥α,∴
⊥α,∴![]()
![]() AM
AM![]()
又AP⊥![]() ,于是在平面β内过点A有两条直线垂直于
,于是在平面β内过点A有两条直线垂直于![]() ,这是不可能的
,这是不可能的![]()
所以AP一定在α内![]()