分段函数的极限和连续性
例 设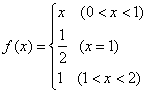
(1)求![]() 在点
在点![]() 处的左、右极限,函数
处的左、右极限,函数![]() 在点
在点![]() 处是否有极限?
处是否有极限?
(2)函数![]() 在点
在点![]() 处是否连续?
处是否连续?
(3)确定函数![]() 的连续区间.
的连续区间.
分析:对于函数![]() 在给定点
在给定点![]() 处的连续性,关键是判断函数当
处的连续性,关键是判断函数当![]() 时的极限是否等于
时的极限是否等于![]() ;函数在某一区间上任一点处都连续,则在该区间上连续.
;函数在某一区间上任一点处都连续,则在该区间上连续.
解:(1)![]()
![]()
∴![]()
函数![]() 在点
在点![]() 处有极限.
处有极限.
(2)![]()
函数![]() 在点
在点![]() 处不连续.
处不连续.
(3)函数![]() 的连续区间是(0,1),(1,2).
的连续区间是(0,1),(1,2).
说明:不能错误地认为![]() 存在,则
存在,则![]() 在
在![]() 处就连续.求分段函数在分界点
处就连续.求分段函数在分界点![]() 的左右极限,一定要注意在分界点左、右的解析式的不同.只有
的左右极限,一定要注意在分界点左、右的解析式的不同.只有![]() 才存在.
才存在.
函数的图象及连续性
例 已知函数![]() ,
,
(1)求![]() 的定义域,并作出函数的图象;
的定义域,并作出函数的图象;
(2)求![]() 的不连续点
的不连续点![]() ;
;
(3)对![]() 补充定义,使其是R上的连续函数.
补充定义,使其是R上的连续函数.
分析:函数![]() 是一个分式函数,它的定义域是使分母不为零的自变量x的取值范围,给函数
是一个分式函数,它的定义域是使分母不为零的自变量x的取值范围,给函数![]() 补充定义,使其在R上是连续函数,一般是先求
补充定义,使其在R上是连续函数,一般是先求![]() ,再让
,再让![]() 即可.
即可.
解:(1)当![]() 时,有
时,有![]() .
.
因此,函数的定义域是![]()
当![]() 时,
时,![]()
其图象如下图.
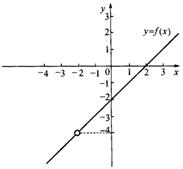
(2)由定义域知,函数![]() 的不连续点是
的不连续点是![]() .
.
(3)因为当![]() 时,
时,![]()
所以![]()
因此,将![]() 的表达式改写为
的表达式改写为
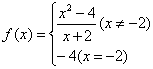
则函数![]() 在R上是连续函数.
在R上是连续函数.
说明:要作分式函数的图象,首先应对函数式进行化简,再作函数的图象,特别要注意化简后的函数与原来的函数定义域是否一致.
利用函数图象判定方程是否存在实数根
例
利用连续函数的图象特征,判定方程![]() 是否存在实数根.
是否存在实数根.
分析:要判定方程![]() 是否有实根,即判定对应的连续函数
是否有实根,即判定对应的连续函数![]() 的图象是否与x轴有交点,因此只要找到图象上的两点,满足一点在x轴上方,另一点在x轴下方即可.
的图象是否与x轴有交点,因此只要找到图象上的两点,满足一点在x轴上方,另一点在x轴下方即可.
解:设![]() ,则
,则![]() 是R上的连续函数.
是R上的连续函数.
又![]() ,因此在
,因此在![]() 内必存在一点
内必存在一点![]() ,使
,使![]() ,所以
,所以![]() 是方程
是方程![]() 的一个实根.
的一个实根.
所以方程![]() 有实数根.
有实数根.
说明:作出函数![]() 的图象,看图象是否与x轴有交点是判别方程
的图象,看图象是否与x轴有交点是判别方程![]() 是否有实数根的常用方法,由于函数
是否有实数根的常用方法,由于函数![]() 是三次函数,图象较难作出,因此这种方法对本题不太适用.
是三次函数,图象较难作出,因此这种方法对本题不太适用.
函数在区间上的连续性
例 函数![]() 在区间(0,2)内是否连续,在区间
在区间(0,2)内是否连续,在区间![]() 上呢?
上呢?
分析:开区间内连续是指内部每一点处均连续,闭区间上连续指的是内部点连续,左点处右连续,右端点处左连续.
解:![]() (
(![]() 且
且![]() )
)
任取![]() ,则
,则![]()
∴ ![]() 在(0,2)内连续.
在(0,2)内连续.
但![]() 在
在![]() 处无定义,∴
处无定义,∴ ![]() 在
在![]() 处不连续.
处不连续.
从而![]() 在
在![]() 上不连线
上不连线
说明:区间上的连续函数其图象是连续而不出现间断曲线.
函数在某一点处的连续性
例 讨论函数![]() 在
在![]() 与
与![]() 点处的连续性
点处的连续性
分析:分类讨论不仅是解决问题的一种逻辑方法,也是一种重要的数学思想.
明确讨论对象,确立分类标准,正确进行分类,以获得阶段性的结论,最后归纳综合得出结果,是分类讨论的实施方法.本题极限式中,若不能对x以1为标准,分三种情况分别讨论,则无法获得![]() 的表达式,使解答搁浅.
的表达式,使解答搁浅.
讨论![]() 在
在![]() 与
与![]() 点处的连续性,若作出
点处的连续性,若作出![]() 的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.
的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.
由于![]() 的表达式并非显式,所以须先求出
的表达式并非显式,所以须先求出![]() 的解析式,再讨论其连续性,其中极限式中含
的解析式,再讨论其连续性,其中极限式中含![]() ,故须分类讨论.
,故须分类讨论.
解:(1)求![]() 的表达式:
的表达式:
①当![]() 时,
时,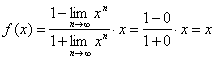
②当![]() 时,
时,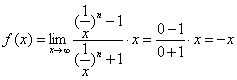
③当![]() 时,
时,![]()
∴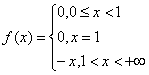
(2)讨论![]() 在
在![]() 点处的连续性:
点处的连续性:
![]()
∴![]() 不存在,
不存在,![]() 在
在![]() 点处不连续
点处不连续
(3)讨论![]() 在
在![]() 点处的连续性:
点处的连续性:
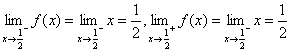
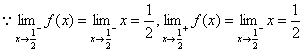
∴![]() ,
,![]() 在
在![]() 点处连续.
点处连续.
根据函数的连续性确定参数的值
例 若函数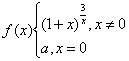 在
在![]() 处连续,试确定a的值
处连续,试确定a的值
解:![]()
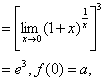
欲![]() 在
在![]() 处连续,
处连续,
必须使![]() ,故
,故![]()
说明:利用连续函数的定义,可把极限转化为函数值求解.