例1计算
。
解法1：原式
解法2：原式
小结：一定要熟记
，
，
，
等。
例2 复数
等于（ ）
A．
B．
C．
D．
分析：
可利用
与
形式非常接近，可考虑
，利用的性质去简化计算．
解：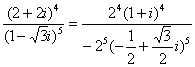
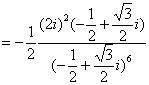
∴ 应选B．
注意：要记住1的立方根，1，
，
，以及它们的性质，对解答有关问题非常有益．
例３ 求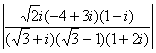
分析1：可将复数式进行乘、除运算化为最简形式，才取模．
解法1：原式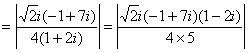
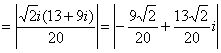
分析2：积或商的模可利用模的性质
，
（
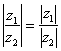）进行运算．
解法2：原式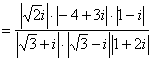
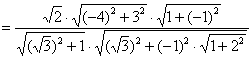
小结：比较解法1和解法2，可以看到后一种解法好．解此类问题应选用后种解法．
例4 已知
是纯虚数，求
在复平面内对应点的轨迹．
分析：利用Z为纯虚数
来解．
解法2：∵
是纯虚数，
∴
（且
，
）
∴ 
，
∴ 
设
（
）
则
（
）
∴ 
的对应点的轨迹以（
，0）为圆心，为半径的圆，并去掉点（0，0）和点（1，0）．
例５ 设为复数，
，那么（ ）
A．
{纯虚数} B．{实数}
C．{实数}
{复数} D．{虚数}
解：∵ 
，即
，
∴ 
，故
，或
所以为实数．
∴ 应选B．
小结：在复数集中，要证复数为实数，只须证我们有如下结论．复数为实数的充要条件是
例６ 若
，
，试求
解：∵ ，
∴ 
又知，
∴ 
设
（
），则
，
∴ 
即
，
由复数相等定义
解得
∴ 
故
小结：下面这些共轭复数运算式，对于解答有关共轭复数问题十分重要，应掌握好．
设（）的共轭复数为
，则：
；
；
；
；
；
；
（
）；
（
）
例７ （1）已知
，
，求证：
（2）已知，，且
求证：
，
中至少有一个是1．
证明：（1）
∴
（2）∵
，∴
即
变形为 
，
或
，可得
，或
，
∴，中至少有一个是1．
小结：掌握好模的性质
（1）
（2）
，，
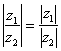（3）
（4）
对解题大有裨益．