1.6 三角函数模型简单应用
一、选择题
1．函数的
最小值为（ ）
A．2 B．0 C．
D．6
2．
，若
，则
的值为（ ）．
A．－a B．2＋a C．2－a D．4－a
3．设A、B都是锐角，且cosA＞sinB则A+B的取值是 （ ）
A．
B．
C．
D．
4．若函数
是奇函数，且当
时，有
，则当
时，的表达式为（ ）
A．
B．
C．
D．
5．下列函数中是奇函数的为( )
A．y=
B．y=
C．y=2cosx D．y=lg(sinx+
)
二、填空题
6．在满足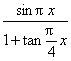
＝0的x中，在数轴上求离点
最近的那个整数值是 ．
7．已知
（其中a、b为常数），若
，则
__________．
8．若
，则锐角
的取值范围是_________．
9．由函数
与函数y＝2的图象围成一个封闭图形，这个封闭图形的面积是_________．
10．函数
的图象关于
轴对称的充要条件是
三、解答题
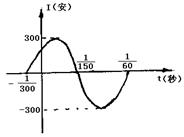
11．如图，表示电流强度I与时间t的关系式
在一个周期内的图象.
|
的解析式
②为了使中t在任意一段
秒的时间内I能同时取最大值A和最小值－A，
那么正整数
的最小值为多少？
12．讨论函数y=lgcos2x的的定义域、值域、奇偶性、周期性和单调性等函数的基本性质
13．函数
的最小值为
（1）求
（2）若
，求
及此时的最大值
14．已知f(x)是定义在R上的函数，且
(1)试证f(x)是周期函数. (2)若f(3)=
，求f(2005)的值.
15．已知函数
是R上的偶函数，其图象关于点
上是单调函数，求
的值．
参考答案
一、选择题
1．Ｂ 2．D 3．C 4．B 5．Ｄ
二、填空题
6．1 7．3 8．
9．
10．
三、解答题
11．（1）
（2）
12．定义域：(kπ-
,kπ+),k∈Z;值域
；奇偶性：偶函数；周期性：周期函数，且T=π;单调性：在(kπ-,kπ
(k∈Z)上递增，在［kπ,kπ+
上递减
13．
(1)函数的最小值为
，
，
，
，
＝
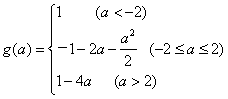
(2)
14．(1)由，故f(x+4)=
=
f(x+8)=f(x+4+4)=
=f(x)，即8为函数
的周期
(2)由 f(x+4) =，得f(5) =
∴f(2005)=f(5+250×8)=f(5)=
15． 由f（x）为偶函数，知f（0）=1,结合
，可求出
．
又由图象关于
对称，知
，即
又
及
．
当k=0,1即
，2时，易验证f（x）在
上单减；k≥2时，f（x）在上不是单调的函数．综上所述