高三文科数学第二次模拟考试试题
一、本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知![]() ,那么角
,那么角![]() 是( )
是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
2.函数![]() 的反函数的定义域为( )
的反函数的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,两条准线与
,两条准线与![]() 轴的交点分别为
轴的交点分别为![]() ,若
,若![]() ,则该椭圆离心率的取值范围是( )
,则该椭圆离心率的取值范围是( )
A.![]() B.
B.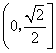 C.
C.![]() D.
D.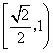
5.在等比数列![]() (
(![]() )中,若
)中,若![]() ,
,![]() ,则该数列的前10项和为( )
,则该数列的前10项和为( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
6.若不等式组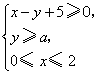 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
7.平面![]() 平面
平面![]() 的一个充分条件是( )
的一个充分条件是( )
A.存在一条直线![]()
B.存在一条直线![]()
C.存在两条平行直线![]()
D.存在两条异面直线![]()
8.对于函数①![]() ,②
,②![]() ,③
,③![]() ,判断如下两个命题的真假:
,判断如下两个命题的真假:
命题甲:![]() 是偶函数;
是偶函数;
命题乙:![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
能使命题甲、乙均为真的所有函数的序号是( )
A.①② B.①③ C.② D.③
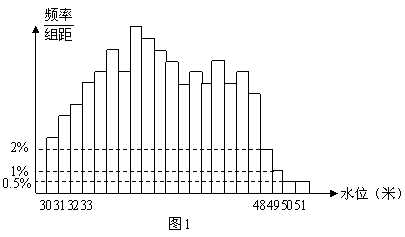
9.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图(如图1).从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是( )
A.48米 B.49米 C.50米 D.51米
10.函数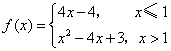 的图象和函数
的图象和函数![]() 的图象的交点个数是( )
的图象的交点个数是( )
A.1 B.2 C.3 D.4
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
11.![]() 是
是![]() 的导函数,则
的导函数,则![]() 的值是 .
的值是 .
12.若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 .
,则此数列的通项公式为 .
13.已知向量![]() .若向量
.若向量![]() ,则实数
,则实数![]() 的值是 .
的值是 .
请考生在14,15两题中任选一题作答,如果多做,则按所做的第一题记分.
14.在极坐标系中,直线![]() 的方程为
的方程为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为 .
的距离为 .
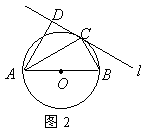
15.如图2所示,圆![]() 的直径
的直径![]() ,
,![]() 为圆周上一点,
为圆周上一点,![]() ,过
,过![]() 作圆的切线
作圆的切线![]() ,过
,过![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() .
.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
 16.(本小题满分14分)
16.(本小题满分14分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,![]() .
.
(Ⅰ)求B的大小;
(Ⅱ)若![]() ,
,![]() ,求b.
,求b.
17.(本小题满分14分)
某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.
18.(本小题满分14分)
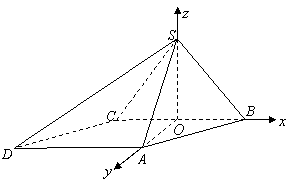
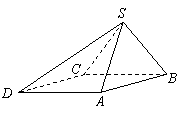 四棱锥
四棱锥![]() 中,底面ABCD为平行四边形,侧面
中,底面ABCD为平行四边形,侧面![]() 底面ABCD,已知
底面ABCD,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)求直线SD与平面SBC所成角的正弦值.
19.(本小题满分14分)
设函数![]() 在
在![]() 及
及![]() 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的![]() ,都有
,都有![]() 成立,求c的取值范围.
成立,求c的取值范围.
20.(本小题满分12分)
设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() ,
,![]()
(Ⅰ)求![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() .
.
21.(本小题满分12分)
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线交椭圆于B,D两点,过
的直线交椭圆于B,D两点,过![]() 的直线交椭圆于A,C两点,且
的直线交椭圆于A,C两点,且![]() ,垂足为P.
,垂足为P.
(Ⅰ)设P点的坐标为![]() ,证明:
,证明:![]() ;
;
(Ⅱ)求四边形ABCD的面积的最小值.
2007-2008年高三文科数学第二次模拟考试试题
参考答案
一、选择题
1.C 2.B 3.B 4.D 5.B 6.C
7.D 8.C 9.C 10.C
二、填空题
11.![]() 12.
12.![]() 13.
13.![]() 14.2 15.30°
14.2 15.30°
三、解答题
16.解:(Ⅰ)由![]() ,根据正弦定理得
,根据正弦定理得![]() ,所以
,所以![]() ,
,
由![]() 为锐角三角形得
为锐角三角形得![]() .………………………………………………7分
.………………………………………………7分
(Ⅱ)根据余弦定理,得![]()
![]()
![]() .
.
所以,![]() .………………………………………………14分
.………………………………………………14分
17.解:(Ⅰ)记![]() 表示事件:“
表示事件:“![]() 位顾客中至少
位顾客中至少![]() 位采用一次性付款”,则
位采用一次性付款”,则![]() 表示事件:“
表示事件:“![]() 位顾客中无人采用一次性付款”.
位顾客中无人采用一次性付款”.
![]() ,
,
![]() .………………………………………………7分
.………………………………………………7分
(Ⅱ)记![]() 表示事件:“
表示事件:“![]() 位顾客每人购买
位顾客每人购买![]() 件该商品,商场获得利润不超过
件该商品,商场获得利润不超过![]() 元”.
元”.
![]() 表示事件:“购买该商品的
表示事件:“购买该商品的![]() 位顾客中无人采用分期付款”.
位顾客中无人采用分期付款”.
![]() 表示事件:“购买该商品的
表示事件:“购买该商品的![]() 位顾客中恰有
位顾客中恰有![]() 位采用分期付款”.
位采用分期付款”.
则![]() .
.
![]() ,
,![]() .
.
![]()
![]()
![]()
![]() .……………………………………14分
.……………………………………14分
18.解法一:(1)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() .
.
 因为
因为![]() ,所以
,所以![]() ,又
,又![]() ,故
,故![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
由三垂线定理,得![]() .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)知![]() ,
,
依题设![]() ,
,
故![]() ,由
,由![]() ,
,![]() ,
,![]() .
.
又![]() ,作
,作![]() ,垂足为
,垂足为![]() ,
,
则![]() 平面
平面![]() ,连结
,连结![]() .
.![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
![]()
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .………………………………………………14分
.………………………………………………14分
解法二:(Ⅰ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() .
.
 又
又![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
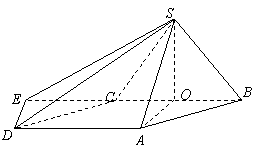
如图,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正向,建立直角坐标系
轴正向,建立直角坐标系![]() ,
,
因为![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .…………………7分
.…………………7分
(Ⅱ)![]() ,
,![]() .
.
![]() 与
与![]() 的夹角记为
的夹角记为![]() ,
,![]() 与平面
与平面![]() 所成的角记为
所成的角记为![]() ,因为
,因为![]() 为平面
为平面![]() 的法向量,所以
的法向量,所以![]() 与
与![]() 互余.
互余.
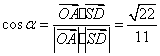 ,
,![]() ,
,
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .………………………14分
.………………………14分
19.解:(Ⅰ)![]() ,
,
因为函数![]() 在
在![]() 及
及![]() 取得极值,则有
取得极值,则有![]() ,
,![]() .
.
即![]()
解得![]() ,
,![]() .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)可知,![]() ,
,
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,又
,又![]() ,
,![]() .
.
则当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
因为对于任意的![]() ,有
,有![]() 恒成立,
恒成立,
所以 ![]() ,
,
解得 ![]() 或
或![]() ,
,
因此![]() 的取值范围为
的取值范围为![]() .………………………14分
.………………………14分
20.解:(Ⅰ)设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则依题意有
,则依题意有![]() 且
且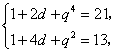
解得![]() ,
,![]() .
.
所以![]() ,
,
![]() .………………………6分
.………………………6分
(Ⅱ)![]() .
.
![]() ,①
,①
![]() ,②
,②
②-①得![]() ,
,
![]()
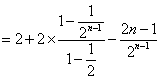
![]() .………………………12分
.………………………12分
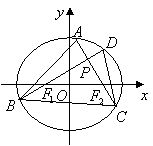 21.证明:(Ⅰ)椭圆的半焦距
21.证明:(Ⅰ)椭圆的半焦距![]() ,
,
由![]() 知点
知点![]() 在以线段
在以线段![]() 为直径的圆上,
为直径的圆上,
故![]() ,
,
所以,![]() .………………………6分
.………………………6分
(Ⅱ)(ⅰ)当![]() 的斜率
的斜率![]() 存在且
存在且![]() 时,
时,![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程![]() ,并化简得
,并化简得![]() .
.
设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
![]() ;
;
因为![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() 的斜率为
的斜率为![]() .
.
所以,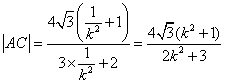 .
.
四边形![]() 的面积
的面积
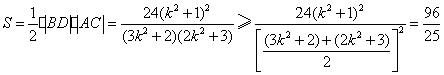 .
.
当![]() 时,上式取等号.………………………10分
时,上式取等号.………………………10分
(ⅱ)当![]() 的斜率
的斜率![]() 或斜率不存在时,四边形
或斜率不存在时,四边形![]() 的面积
的面积![]() .……………………11分
.……………………11分
综上,四边形![]() 的面积的最小值为
的面积的最小值为![]() .………………………12分
.………………………12分