高三理科数学教学质量抽测试题
本试卷共4页,21小题,满分150分.考试用时120分钟.
注意事项:
1.答选择题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、考试科目填写在答题卡上,并用2B铅笔将相应的信息点涂黑.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]() .
.
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() .
.
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么在
,那么在![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]() .
.
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合![]() 的真子集的个数为
的真子集的个数为
A.6 B.7 C.8 D.9
2.不等式![]() 的解集是
的解集是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的一个单调递增区间为
的一个单调递增区间为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设复数![]() 满足
满足![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知向量![]() ,
,![]() ,若
,若![]() ,则
,则![]()
 A.
A.![]() B.
B.![]()
C.1 D.3
6.如图1所示,是关于判断闰年的流程图,则以
下年份是闰年的为
A.1996年
B.1998年
C.2010年
D.2100年
7.已知![]() ,
,![]() 是平面,
是平面,![]() ,
,![]() 是直线,给出下
是直线,给出下
列命题
①若![]() ,
,![]() ,则
,则![]() .
.
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
③如果![]() 、n是异面直线,那么
、n是异面直线,那么![]() 相交.
相交.
④若![]() ,
,![]() ∥
∥![]() ,且
,且![]() ,则
,则![]() ∥
∥![]() 且
且![]() ∥
∥![]() .
.
其中正确命题的个数是
A.4 B.3 C.2 D.1
8.函数![]() ,若
,若![]() (其中
(其中![]() 、
、![]() 均大于2),则
均大于2),则![]() 的最小值为
的最小值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9.某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人.
10.已知等比数列![]() 的前三项依次为
的前三项依次为![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
11.抛物线![]() 上一点
上一点![]() 到焦点的距离为3,则点
到焦点的距离为3,则点![]() 的横坐标
的横坐标![]() .
.
12.已知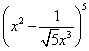 的展开式中的常数项为
的展开式中的常数项为![]() ,
,![]() 是以
是以![]() 为周期的偶函数,且当
为周期的偶函数,且当![]() 时,
时,![]() ,若在区间
,若在区间![]() 内,函数
内,函数![]() 有4个零点,则实数
有4个零点,则实数![]() 的取值范围是 .
的取值范围是 .
 13.(坐标系与参数方程选做题)在极坐标系中,点
13.(坐标系与参数方程选做题)在极坐标系中,点![]() 到直线
到直线![]() 的距离为
.
的距离为
.
14.(不等式选讲选做题)不等式![]() 的解集
的解集
是 .
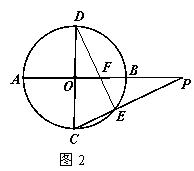
15.(几何证明选讲选做题)如图2所示,![]() 与
与![]() 是
是![]() 的直径,
的直径,![]()
![]()
![]() ,
,![]() 是
是![]() 延长线上一点,连
延长线上一点,连![]() 交
交![]() 于点
于点![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
在△![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
17.(本小题满分12分)
已知射手甲射击一次,击中目标的概率是![]() .
.
(1)求甲射击5次,恰有3次击中目标的概率;
(2)假设甲连续2次未击中目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率.
 18.(本小题满分14分)
18.(本小题满分14分)
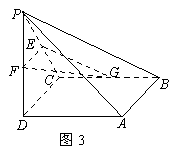
如图3所示,四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为
![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角D-FG-E的余弦值.
19.(本小题满分14分)
设函数![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数![]() 的取值范围.
的取值范围.
20.(本小题满分14分)
已知点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() 相交于点M,且它们的斜率之积为
相交于点M,且它们的斜率之积为![]() .
.
(1)求点M轨迹![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() (
(![]() 在
在![]() 、
、![]() 之间),试求
之间),试求![]() 与
与![]() 面积之比的取值范围(
面积之比的取值范围(![]() 为坐标原点).
为坐标原点).
21.(本小题满分14分)
已知数列![]() 中,
中,![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足
![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
参考答案及评分标准
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | C | D | A | D | A | C | B |
8.方法1:由![]() ,得
,得![]() ,
,
即![]() .
.
于是![]() ,
,
所以![]() .
.
方法2:由![]() ,得
,得![]() ,
,
即![]() .
.
于是![]() ,
,
则![]() (其中
(其中![]() ),再利用导数的方法求解.
),再利用导数的方法求解.
二、填空题:本大题主要考查基本知识和基本运算.共7小题,每小题5分,满分30分.
9.760 10.![]() 11.2
12.
11.2
12.![]()
13.![]() 14.
14.![]() 15.3
15.3
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
(本小题主要考查正弦定理、余弦定理、解三角形等基础知识,考查运算求解能力)
解:(1)由余弦定理,![]() ,………………………………………2分
,………………………………………2分
得![]() ,…………………………………………………4分
,…………………………………………………4分
![]()
![]() .……………………………………………………………………………6分
.……………………………………………………………………………6分
(2)方法1:由余弦定理,得![]() ,………………………………8分
,………………………………8分
![]() ,………………………10分
,………………………10分
∵![]() 是
是![]() 的内角,
的内角,
∴![]() .………………………………………………………12分
.………………………………………………………12分
方法2:∵![]() ,且
,且![]() 是
是![]() 的内角,
的内角,
∴![]() .………………………………………………………8分
.………………………………………………………8分
根据正弦定理,![]() ,……………………………………………………10分
,……………………………………………………10分
得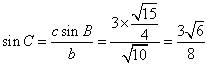 . ……………………………………………12分
. ……………………………………………12分
17.(本小题满分12分)
(本小题主要考查独立重复试验等基础知识,考查或然与必然的数学思想与方法,以及运算求解能力)
解:(1)设“甲射击5次,恰有3次击中目标”为事件A,则
![]() .
.
答:甲射击5次,恰有3次击中目标的概率为![]() .………………………………6分
.………………………………6分
(2)方法1:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
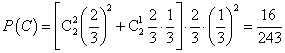 .
.
答:甲恰好射击5次后,被中止射击的概率为![]() .……………………………12分
.……………………………12分
方法2:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
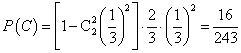 .
.
答:甲恰好射击5次后,被中止射击的概率为![]() .……………………………12分
.……………………………12分
18.(本小题满分14分)
(本小题主要考查空间中线面关系,二面角及其平面角、坐标方法的运用等基础知识,考查数形结合的数学思想和方法,以及空间想象能力、逻辑推理能力和运算求解能力)
(1)证法1:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 为正方形,∴
为正方形,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .……………………………………………3分
.……………………………………………3分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .…………………………………………………………6分
.…………………………………………………………6分
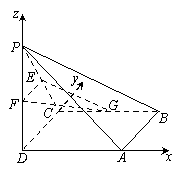
证法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
…………………………………………………4分
 ∵
∵![]() ,
,
∴![]() .………………………………………6分
.………………………………………6分
(2)解法1:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .………………………………8分
.………………………………8分
设平面DFG的法向量为![]() ,
,
∵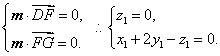
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.…………………………10分
的一个法向量.…………………………10分
设平面EFG的法向量为![]() ,
,
∵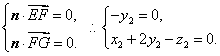
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.……………………………12分
的一个法向量.……………………………12分
∵![]() .
.
设二面角![]() 的平面角为θ,则
的平面角为θ,则![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .………………………………………14分
.………………………………………14分
解法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .………………………………8分
.………………………………8分
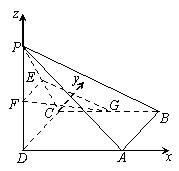 过
过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() ,解得
,解得![]() .
.
∴![]() .…………10分
.…………10分
再过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() ,解得
,解得![]() .
.
∴![]() .……………………………………………12分
.……………………………………………12分
∴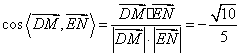 .
.
∵![]() 与
与![]() 所成的角就是二面角
所成的角就是二面角![]() 的平面角,
的平面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .………………………………………14分
.………………………………………14分
19.(本小题满分14分)
(本小题主要考查函数、微积分基本定理和导数的应用,考查综合运用数学知识分析和解决问题的能力)
解:(1)函数![]() 的定义域为
的定义域为![]() ,…………………………………………………1分
,…………………………………………………1分
∵![]() ,………………………………………2分
,………………………………………2分
∵![]() ,则使
,则使![]() 的
的![]() 的取值范围为
的取值范围为![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() . ……………………………………………4分
. ……………………………………………4分
(2)方法1:∵![]() ,
,
∴![]() .…………………………6分
.…………………………6分
令![]() ,
,
∵![]() ,且
,且![]() ,
,
由![]() .
.
∴![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,……………………9分
内单调递增,……………………9分
故![]() 在区间
在区间![]() 内恰有两个相异实根
内恰有两个相异实根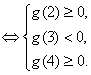 ……12分
……12分
即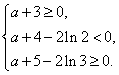 解得:
解得:![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .………………………………14分
.………………………………14分
方法2:∵![]() ,
,
∴![]() .…………………………6分
.…………………………6分
即![]() ,
,
令![]() ,
,
∵![]() ,且
,且![]() ,
,
由![]() .
.
∴![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.……………………9分
内单调递减.……………………9分
∵![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
故![]() 在区间
在区间![]() 内恰有两个相异实根
内恰有两个相异实根![]() .
.
……………………………………12分
即![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() . ……………………………14分
. ……………………………14分
20.(本小题满分14分)
(本小题主要考查椭圆的概念、椭圆的方程等基础知识,考查待定系数法、数形结合的数学思想与方法,以及运算求解能力)
解:(1)设点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,∴
,∴![]() . ………………………………………2分
. ………………………………………2分
整理,得![]() (
(![]() ),这就是动点M的轨迹方程.……………………4分
),这就是动点M的轨迹方程.……………………4分
(2)方法1:如图,由题意知直线![]() 的斜率存在,
的斜率存在,
设![]() 的方程为
的方程为![]() (
(![]() ) …… ①…………………………………5分
) …… ①…………………………………5分
将①代入![]() ,
,
得![]() ,
,
………………6分
由![]() ,解得
,解得![]() .…………………………………………………………7分
.…………………………………………………………7分
设![]() ,
,![]() ,则
,则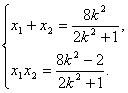 …… ② ……………………8分
…… ② ……………………8分
令![]() ,则
,则![]() ,即
,即![]() ,即
,即![]() ,且
,且![]()
……………………9分
由②得,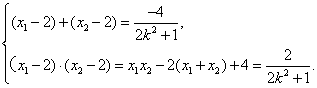
即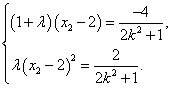
![]() .……………………………………………11分
.……………………………………………11分
![]() 且
且![]()
![]() 且
且![]() .
.
解得![]() 且
且![]() ………………………………………………13分
………………………………………………13分
![]() ,
,![]() 且
且![]() .
.
∴△OBE与△OBF面积之比的取值范围是![]() .……………14分
.……………14分
方法2:如图,由题意知直线![]() 的斜率存在,
的斜率存在,
设![]() 的方程为
的方程为![]()
![]() …… ①…………5分
…… ①…………5分
将①代入![]() ,
,
整理,得![]() ,…………6分
,…………6分
由![]() ,解得
,解得![]() .………………………………………………………………7分
.………………………………………………………………7分
设![]() ,
,![]() ,则
,则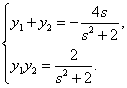 …… ② ……………………8分
…… ② ……………………8分
令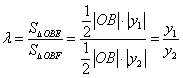 ,且
,且![]() .…………………………………9分
.…………………………………9分
将![]() 代入②,得
代入②,得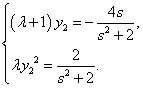
∴![]() .即
.即![]() .……………………………………11分
.……………………………………11分
∵![]() 且
且![]() ,∴
,∴![]() 且
且![]() .
.
即![]() 且
且![]() .
.
解得![]() 且
且![]() .……………………………………………13分
.……………………………………………13分
![]() ,
,![]() 且
且![]() .
.
故△OBE与△OBF面积之比的取值范围是![]() .……………14分
.……………14分
21.(本小题满分14分)
(本小题主要考查等差数列、不等式及其性质等基础知识,考查分类讨论、化归与转化的数学思想方法,以及抽象概括能力、运算求解能力)
解:(1)由已知,![]() (
(![]() ,
,![]() ), …………………2分
), …………………2分
即![]() (
(![]() ,
,![]() ),且
),且![]() .
.
∴数列![]() 是以
是以![]() 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴![]() .……………………………………………………………………………4分
.……………………………………………………………………………4分
(2)∵![]() ,∴
,∴![]() ,要使
,要使![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
∴![]() 恒成立.……………………………………………………………6分
恒成立.……………………………………………………………6分
(ⅰ)当![]() 为奇数时,即
为奇数时,即![]() 恒成立,…………………………………………7分
恒成立,…………………………………………7分
当且仅当![]() 时,
时,![]() 有最小值为1,
有最小值为1,
∴![]() .………………………………………………………………………………9分
.………………………………………………………………………………9分
(ⅱ)当![]() 为偶数时,即
为偶数时,即![]() 恒成立,………………………………………10分
恒成立,………………………………………10分
当且仅当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
∴![]() .……………………………………………………………………………12分
.……………………………………………………………………………12分
即![]() ,又
,又![]() 为非零整数,则
为非零整数,则![]() .
.
综上所述,存在![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() .…………………14分
.…………………14分