高三理科数学第一学期期末考试试题
数 学 试 题(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,满分150分钟,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1、答第Ⅰ卷前,考生务必将自己的姓名、学号、学校、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3、考试结束后,监考人员将本试卷和答题卡一并收回。
参考公式:
球的表面积公式 球的体积公式
![]()
![]()
其中![]() 表示球的半径
其中
表示球的半径
其中![]() 表示球的半径
表示球的半径
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数![]() 的定义域是
的定义域是
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.-7
D.7
C.-7
D.7
3.已知直线![]() 与直线
与直线![]() 互相垂直,则实数
互相垂直,则实数![]() 为
为
A.![]() B.0或
B.0或![]()
4.在等比数列![]() 中,已知
中,已知![]() ,则
,则![]() 的值为
的值为
A.16
B.
5.在![]() 中,已知
中,已知![]() ,那么
,那么![]() 一定是
一定是
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
6.设![]() 、
、![]() 是两条不同的直线
是两条不同的直线![]() 、
、![]() 、
、![]() 是三个不同的平面,给出下列四个命题;①若
是三个不同的平面,给出下列四个命题;①若![]() 则
则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() 。其中正确命题的个数是
。其中正确命题的个数是
A.0
B.
7.若奇函数![]() ,满足
,满足![]() ,则
,则![]() 等于
等于
A.0
B.![]() D.
D.![]()
8.一个几何体的三视图如下所示,则该几何体的表面积是
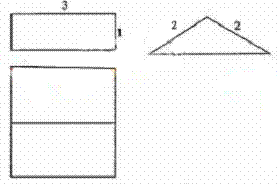
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的图象大致形状是
的图象大致形状是
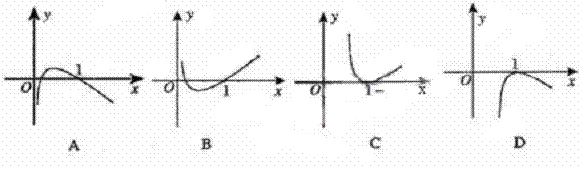
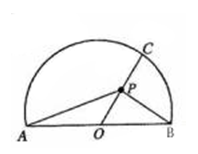 10.如图,半圆的直径
10.如图,半圆的直径![]() 为圆心,
为圆心,![]() 是半圆上不同于
是半圆上不同于![]() 、
、![]() 的任意一点。若
的任意一点。若![]() 为半径
为半径![]() 上的动点,则
上的动点,则![]() 的最小值是
的最小值是
A.2 B.0
C.-1 D.-2
11.已知实系数方程![]() 的两个实根分别为
的两个实根分别为![]() 、
、![]() ,且
,且![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.若实数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
注意事项:
1、第Ⅱ卷共7页,用钢笔或圆珠笔答在试题中(除题目有特殊规定外)。
2、答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4个小题,每小题4分,共16分。请据答案填在题中横线上。
13.在直角坐标平内面,由直线![]() 和抛物线
和抛物线![]() 所围成的平面区域的面积是__________________。
所围成的平面区域的面积是__________________。
14.设![]() 定义如下面读数表,
定义如下面读数表,![]() 满足
满足![]() ,且对任意自然数
,且对任意自然数![]() 均有
均有![]() ,则
,则![]() 的值为___________________。
的值为___________________。
|
| 1 | 2 | 3 | 4 | 5 |
|
| 4 | 1 | 3 | 5 | 2 |
15.已知点![]() 在圆
在圆![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点也在圆
的对称点也在圆![]() 上,则
上,则![]() 。
。
16.已知函数![]() ,给出下列命题:
,给出下列命题:
①![]() 不可能为奇函数;
不可能为奇函数;
②当![]() 时,
时,![]() 的图象必关于直线
的图象必关于直线![]() 对称;
对称;
③若![]() ,则
,则![]() 在区间
在区间![]() 上是增函数;
上是增函数;
④![]() 的最小值
的最小值![]() ,
,
其中正确命题的序号是_____________(把你认为正确的序号都填上)。
三、解答题:本大题共6个小题,满分74分。解答应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知向量![]() ,设函数
,设函数![]() 。
。
(Ⅰ)求![]() 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(Ⅱ)在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是角
分别是角![]() 、
、![]() 、
、![]() 的对边,若
的对边,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值。
的值。
18.(本小题满分12分)
已知命题![]() 和
和![]() 是方程
是方程![]() 的两个实根,不等式
的两个实根,不等式![]() 对任意实数
对任意实数![]() 恒成立;命题
恒成立;命题![]() 不等式
不等式![]() 有解;若命题
有解;若命题![]() 是真命题,命题
是真命题,命题![]() 是假命题,求
是假命题,求![]() 的取值范围。
的取值范围。
19.(本小题满分12分)
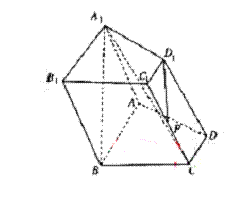 如图,已知四棱柱
如图,已知四棱柱![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,侧面
,侧面![]() 为正方形,点
为正方形,点![]() 为棱
为棱![]() 的中点。
的中点。
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正切值。
的正切值。
20.(本小题满分12分)
甲、乙两大超市同时开业,第一年的全年销售额为a万元,由于经营方式不同,甲超市前n年的总销售额为![]() 万元,乙超市第
万元,乙超市第![]() 年的销售额比前一年销售客多
年的销售额比前一年销售客多![]() 万元。
万元。
(Ⅰ)求甲、乙两超市第![]() 年销售额的表达式;
年销售额的表达式;
(Ⅱ)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年。
21.(本小题满分12分)
已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围。
的取值范围。
22.(本小题满分14分)
设函数![]() ,其中
,其中![]() 。
。
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,证明不等式:
时,证明不等式:![]() ;
;
(Ⅲ)设![]() 的最小值为
的最小值为![]() ,证明不等式:
,证明不等式:![]() ;
;
参考答案
一、选择题:本题共12个小题,每小题5分,共60分。
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | C | A | B | A | B | C | D | C | A | D | A | C |
二、填空题:本题共4个小题,每小题4分,共16分。
13.![]() 14.4 15.
14.4 15.![]() 16.①③
16.①③
三、解答题:本题共6个小题,共74分。
17.(本小题满分12分)
解:(Ⅰ)![]() ,
,
![]()
![]()
![]()
![]() ……3分
……3分
![]() ……4分
……4分
令![]()
![]()
![]() 的单调区间为
的单调区间为![]() ……6分
……6分
(Ⅱ)由![]() 得
得
![]()
![]()
又![]() 为
为![]() 的内角
的内角
![]()
![]()
![]() ……8分
……8分
![]()
![]()
![]() ……8分
……8分
![]()
![]() ……12分
……12分
18.(本小题满分12分)
解:![]() 、
、![]() 是方程
是方程![]() 的两个实根
的两个实根
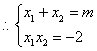
![]() ……3分
……3分
∴当![]() 时,
时,![]() ……4分
……4分
由不等式![]() 对任意实数
对任意实数![]() 恒成立可得:
恒成立可得:
![]()
![]() 或
或![]()
∴命题![]() 为真命题时
为真命题时![]() 或
或![]() ……6分
……6分
命题![]() 不等式
不等式![]() 有解
有解
①当![]() 时,显然有解
时,显然有解
②当![]() 时,
时,![]() 有解……8分
有解……8分
③当![]() 时,
时,![]() 有解
有解
![]()
![]()
从而命题![]() 不等式
不等式![]() 有解时
有解时![]() ……10分
……10分
又命题![]() 是假命题
是假命题
![]() ……11分
……11分
故命题![]() 是真假题且命题
是真假题且命题![]() 是假命题时,
是假命题时,![]() 的取值范围为
的取值范围为
![]() ……12分
……12分
19.(本小题满分12分)
(Ⅰ)证明:如图:延长![]() 、
、![]() 相交于
相交于![]() ,连结
,连结![]() 。
。
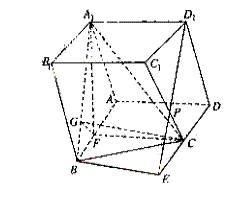 ∵点
∵点![]() 为
为![]() 的中点
的中点
![]()
故![]()
又![]() 且
且![]()
![]()
从而四边形![]() 为平行四边形……2分
为平行四边形……2分
![]()
又![]()
故四边形![]() 是平行四边形……4分
是平行四边形……4分
从而![]()
又![]() 平面
平面![]()
![]() ……5分
……5分
(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]()
![]()
![]() 平面
平面![]()
又![]() 为
为![]() 的中点且
的中点且![]()
![]()
故![]() 平面
平面![]() ……7分
……7分
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() 。
。
![]() 为二面角
为二面角![]() 的平面角……9分
的平面角……9分
在正![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为直角三角形
为直角三角形
设![]()
从而![]() ,
,
在![]() 中,
中,![]() ……11分
……11分
从而,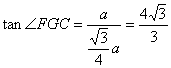 ……12分
……12分
20.(本小题满分12分)
解:(Ⅰ)设甲、乙超市第![]() 年销售额分别为
年销售额分别为![]() ,又设甲超市前
,又设甲超市前![]() 年总销售额为
年总销售额为![]() ,
,
则![]() 。
。
因![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() ……3分
……3分
又因![]() 时
时![]() ,……4分
,……4分
故![]()
![]()
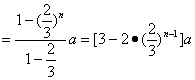 。
。
显然![]() 也适合,故
也适合,故![]() 。……7分
。……7分
(Ⅱ)当![]() 时,
时,![]() ,有
,有![]() ;
;
![]() 时,
时,![]() ,有
,有![]() ;
;
当![]() 时,
时,![]() ,而
,而![]() ,故乙超市有可能被收购。……9分
,故乙超市有可能被收购。……9分
当![]() 时,令
时,令![]() ,
,
则![]() ,
,
即![]() 。……10分
。……10分
又当![]() 时
时![]() ,
,
故当![]() 且
且![]() 时,必有
时,必有![]() 。
。
即第7年乙超市的年销售额不足甲超市的一半,乙超市将被甲超市收购。……12分
21.(本小题满分12分)
解:(Ⅰ)由题意椭圆的离心率![]() 。
。
![]()
![]()
![]()
∴椭圆方程为![]() ……2分
……2分
又点![]() 在椭圆上
在椭圆上
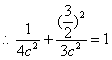
![]()
∴椭圆的方程为![]() ……4分
……4分
(Ⅱ)设![]()
由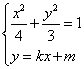
消去![]() 并整理得
并整理得![]() ……6分
……6分
∵直线![]() 与椭圆有两个交点
与椭圆有两个交点
![]() ,即
,即![]() ①……7分
①……7分
又![]()
![]() 中点
中点![]() 的坐标为
的坐标为![]() ……8分
……8分
设![]() 的垂直平分线
的垂直平分线![]() 方程:
方程:![]()
![]() 在
在![]() 上
上
![]()
即![]()
![]() ……10分
……10分
将上式代入①得![]()
![]()
即![]() 或
或![]()
![]() 的取值范围为
的取值范围为![]() ……12分
……12分
22.(本小题满分14分)
解:(Ⅰ)由已知得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
![]() ,解得
,解得![]() ……2分
……2分
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + |
|
| ↘ | 极小值 | ↗ |
由上表可知,当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内单调递减,……3分
内单调递减,……3分
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内单调递增,……4分
内单调递增,……4分
所以,函数![]() 的单调减区间是
的单调减区间是![]() ,函数
,函数![]() 的单调增区间是
的单调增区间是![]() 。……5分
。……5分
(Ⅱ)设![]() 。
。
对![]() 求导,得:
求导,得:![]() 。……7分
。……7分
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内是增函数。所以
内是增函数。所以![]() 在
在![]() 上是增函数。
上是增函数。
当![]() 时,
时,![]() ,即
,即![]() 。……9分
。……9分
同理可证![]() <x。……9分
<x。……9分
(Ⅲ)由(Ⅰ)知,![]() ,……11分
,……11分
将![]() 代入
代入![]() ,
,
得: ![]()
即:1<(a+1)![]() ,……13分
,……13分
![]() ,即
,即![]() 。……14分
。……14分
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
|
|
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||