高三数学第一学期期末联考试卷(理科)
![]() 第I卷(选择题,共50分)
第I卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设A、B为两个非空子集,定义:![]() ,若A={0,2,5}, B={1,2,6},则A+B子集的个数是 ( )
,若A={0,2,5}, B={1,2,6},则A+B子集的个数是 ( )
A、29 B、28 C、27 D、26
2、![]() 是虚数单位,复数
是虚数单位,复数![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、将![]() 的图象按向量
的图象按向量![]() ,
,![]() )平移,则平移后所得图象的解析式为( )。
)平移,则平移后所得图象的解析式为( )。
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4、已知直线![]() 、
、![]() 及平面
及平面![]() ,下列命题中的真命题是( )
,下列命题中的真命题是( )
A、若![]() ,
,![]() ,则
,则![]() ∥
∥![]() B、若
B、若![]() ∥
∥![]() ,
,![]() ,则
,则![]() ∥
∥![]()
C、若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() D、若
D、若![]() ,
,![]() ,则
,则![]() ∥
∥![]()
5、若以连续掷两次骰子分别得到的点数![]() 、
、![]() 作为点P的横、纵坐标,则点P在直线
作为点P的横、纵坐标,则点P在直线![]() 下方的概率是( )
下方的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,
,![]() 的值等于( )
的值等于( )
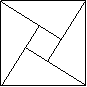 A、1 B、
A、1 B、![]()
C、![]() D、-
D、-![]()
7、函数![]() 的图象大致是(
)
的图象大致是(
)
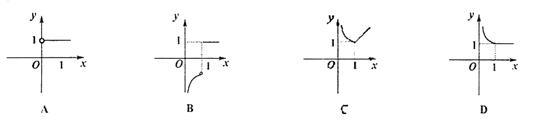
8、在![]() 的展开式中含有常数项,则正整数
的展开式中含有常数项,则正整数![]() 的最小值是( )
的最小值是( )
A、4 B、5 C、6 D、7
9、椭圆![]() (
(![]() >
>![]() >
>![]() )的离心率为
)的离心率为![]() ,右焦点为F(
,右焦点为F(![]() ,
,![]() ),方程
),方程![]() 的两个实根分别为
的两个实根分别为![]() ,
,![]() ,则点
,则点![]() ( )
( )
A、必在圆![]() 内 B、必在圆
内 B、必在圆![]() 上
上
C、必在圆![]() 外 D、以上三种情形都有可能
外 D、以上三种情形都有可能
10、定义运算:![]() ,如
,如![]() ,则函数
,则函数![]() 的值域为(
)
的值域为(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
![]() 第II卷(非选择题100分)
第II卷(非选择题100分)
二、填空题:本大题共7小题,每小题4分,共28分。把答案填在题目中横线上。
11、若已知随机变量§的分布列为
| § | 0 | 1 | 2 | 3 | 4 |
| p | 0.1 | 0.2 | 0.3 |
| 0.1 |
则![]() = E§=
= E§=
12、若![]() ,
,![]() ,
,![]() (
(![]() ,4 ),
,4 ),![]() ∥
∥![]() ,则
,则![]() 的值是
。
的值是
。
13、在数列![]() 中,若
中,若![]() ,
,![]() ,
,![]() 则该数列的通项
则该数列的通项![]() = 。
= 。
14、在![]() 的二面角内,放一个半径为10cm的球切两半平面于A、B两点,那么两切点在球面上的最短距离是
。
的二面角内,放一个半径为10cm的球切两半平面于A、B两点,那么两切点在球面上的最短距离是
。
15、双曲线![]() (
(![]() >0,
>0,![]() >
>![]() )的离心率为2,有一个焦点与抛物线
)的离心率为2,有一个焦点与抛物线![]() 的焦点重合,则
的焦点重合,则![]() 的值为 。
的值为 。
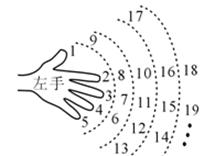 16、 在小时候,我们就用手指练习过数数. 一个小朋友按如图所示的规则练习数数,数到2008时对应的指头是 。
16、 在小时候,我们就用手指练习过数数. 一个小朋友按如图所示的规则练习数数,数到2008时对应的指头是 。
(填出指头的名称,各指头的名称依次为大拇指、食指、中指、
无名指、小指).
17、任取集合![]() ,
,![]() ,
,![]() ,
,![]() ,……,14}中的三个不同数
,……,14}中的三个不同数![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ≥3,
≥3,![]() ≥2,则选取这样的三个数方法种数共有
。(用数字作答)
≥2,则选取这样的三个数方法种数共有
。(用数字作答)
三、解答题:本大题共5小题,共72分,写出文字说明,证明或演算步骤。
18、(本小题满分14分)已知:A、B、C是△ABC的三个内角,向量![]() ,
,![]() ),
),![]() ,
,![]() ),且
),且![]() 。
。
(1)求角A。
(2)若![]() ,求
,求![]() 。
。
 19、(本小题满分14分)右图是一个直三棱柱(以
19、(本小题满分14分)右图是一个直三棱柱(以![]() 为底面),被一平面所截得的几何体,截面为ABC。已知
为底面),被一平面所截得的几何体,截面为ABC。已知![]() ,∠
,∠![]() ,
,![]() ,
,![]() ,
,![]()
(I)设点O是AB的中点,证明:![]() ∥平面
∥平面![]()
(II)求AB与平面![]()
![]() 所成角的大小。
所成角的大小。
20. (本小题满分14分)已知函数![]() (a为实常数). (1) 当a =
0时,求函数
(a为实常数). (1) 当a =
0时,求函数![]() 的最小值;
的最小值;
(2) 若函数![]() 在
在![]() 上是单调函数,求a的取值范围。
上是单调函数,求a的取值范围。
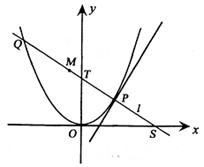
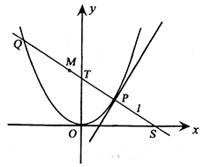 21、(本小题满分15分)如图,P是抛物线
21、(本小题满分15分)如图,P是抛物线![]() :
:![]() 上一点,直线
上一点,直线![]() 过点P且与抛物线C交于另一点Q。
过点P且与抛物线C交于另一点Q。
(1)若直线![]() 与过点
与过点![]() 的切线垂直,求线段PQ中点M的轨迹方程。
的切线垂直,求线段PQ中点M的轨迹方程。
(2)若直线![]() 不过原点且与
不过原点且与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,试求
,试求![]() 的取值范围。
的取值范围。
22、(本小题满分15分)
已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的实数
成立的实数![]() 只有一个。
只有一个。
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,证明:数列
,证明:数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明:![]() ,
,![]() 。
。

数学答题卷(理科)
一、选择题(每题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每题4分,共28分)
11、 12、
13、 14、
15、 16、
17、
三、解答题(本大题共有5小题)
18、(本小题满分14分)已知:A、B、C是△ABC的三个内角,向量![]() ,
,![]() ),
),![]() ,
,![]() ),且
),且![]() 。
。
(1)求角A。
(2)若![]() ,求
,求![]() 。
。
 19、(本小题满分14分)右图是一个直三棱柱(以
19、(本小题满分14分)右图是一个直三棱柱(以![]() 为底面),被一平面所截得的几何体,截面为ABC。已知
为底面),被一平面所截得的几何体,截面为ABC。已知![]() ,∠
,∠![]() ,
,![]() ,
,![]() ,
,![]()
(I)设点O是AB的中点,证明:![]() ∥平面
∥平面![]()
(II)求AB与平面![]()
![]() 所成角的大小。
所成角的大小。
20、
(本小题满分14分)已知函数![]() (a为实常数).
(a为实常数).
(1)当a =
0时,求函数![]() 的最小值;
的最小值;
(2)若函数![]() 在
在![]() 上是单调函数,求a的取值范围。
上是单调函数,求a的取值范围。
 21、(本小题满分15分)如图,P是抛物线
21、(本小题满分15分)如图,P是抛物线![]() :
:![]() 上一点,直线
上一点,直线![]() 过点P且与抛物线C交于另一点Q。
过点P且与抛物线C交于另一点Q。
(1)若直线![]() 与过点
与过点![]() 的切线垂直,求线段PQ中点M的轨迹方程。
的切线垂直,求线段PQ中点M的轨迹方程。
(2)若直线![]() 不过原点且与
不过原点且与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,试求
,试求![]() 的取值范围。
的取值范围。
22、(本小题满分15分)
已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的实数
成立的实数![]() 只有一个。
只有一个。
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,证明:数列
,证明:数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明:![]() ,
,![]() 。
。
参考答案
1.B 2.A 3.A 4.D 5.C 6.D 7.D 8.B 9.A 10.C
11.0.3 2.1
12.![]() 13.
13.![]() 14。
14。 ![]()
![]() cm 15.
cm 15. ![]() 16.食指
16.食指
17.165
18.解:(1)∵![]() ,
,![]() 且
且![]() ,
,
∴![]() …………………………(3分)
…………………………(3分)
∴![]()
即![]() ……………………………………(5分)
……………………………………(5分)
∵ ![]()
∴![]() ………………………………………………(7分)
………………………………………………(7分)
(2)由题意,得![]()
∴![]()
即![]()
∴![]() ………………………………………………10分
………………………………………………10分
∵![]()
![]()
∴![]() ………………………………14分
………………………………14分
19.解: 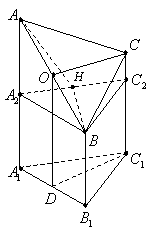 (Ⅰ)证明:作
(Ⅰ)证明:作![]() 交
交![]() 于
于![]() ,连
,连![]() .
.
则![]() ,
,
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
则![]() 是平行四边形,因此有
是平行四边形,因此有![]() ,
,
![]() 平面
平面![]() ,且
,且![]() 平面
平面![]()
则![]() 面
面![]() .
……………….7分
.
……………….7分
(Ⅱ)解:如图,过![]() 作截面
作截面![]() 面
面![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() ,
,![]() ,
,
作![]() 于
于![]() ,
,
因为平面![]() 平面
平面![]() ,则
,则![]() 面
面![]() .
.
连结![]() ,则
,则![]() 就是
就是![]() 与面
与面![]() 所成的角.
所成的角.
因为![]() ,
,![]() ,所以
,所以![]() .
.
![]() 与面
与面![]() 所成的角为
所成的角为![]() .……………….14分
.……………….14分
解法二:
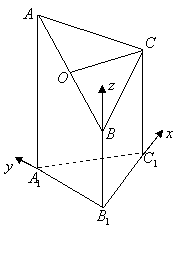
(Ⅰ)证明:如图,以![]() 为原点建立空间直角坐标系,则
为原点建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,因为
,因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
![]() ,
,
易知,![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由![]() 且
且![]() 平面
平面![]() 知
知![]() 平面
平面![]() .
.
……………….7分
(Ⅱ)设![]() 与面
与面![]() 所成的角为
所成的角为![]() .
.
求得![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,则由
的一个法向量,则由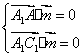 得
得![]() ,
,
取![]() 得:
得:![]() .
.
又因为![]()
所以,![]() ,
,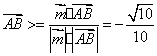 则
则![]() .
.
所以![]() 与面
与面![]() 所成的角为
所成的角为![]() .……………….14分
.……………….14分
20. 解:(1)a = 0时,![]() …………………………………..2分
…………………………………..2分
当0<x<1时![]() ,
,
当x>1时![]() ,…………………………………………..5分
,…………………………………………..5分
∴![]() …………………………………………….7分
…………………………………………….7分
(2)![]()
当a≥0时,![]() 在[2,+∞)上恒大于零,即
在[2,+∞)上恒大于零,即![]() ,符合要求;…… 10分
,符合要求;…… 10分
当a<0时,令![]() ,g (x)在[2,+∞)上只能恒小于零
,g (x)在[2,+∞)上只能恒小于零
故△=1+4a≤0或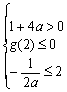 ,解得:a≤
,解得:a≤![]()
∴a的取值范围是![]() ……………………………………………14分
……………………………………………14分
21、解:(1)设![]() ,
,![]() ,
,![]() ,依题意
,依题意![]() ,
,![]() ,
,![]() ,
,
由已知可得 ![]() ①
① ![]() 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
∴过点P的切线的斜率![]()
![]() ,∵
,∵![]() ,
,
∴直线![]() 的斜率
的斜率![]() ,
,
∴直线![]() 的方程为
的方程为![]() ②。。。。。。。。。。。。。。。。。。。。。。。。。4分
②。。。。。。。。。。。。。。。。。。。。。。。。。4分
[解法一] 联立①②消去![]() ,得
,得![]() 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分
∵M是PQ的中点,
∴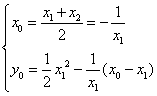 ,消去
,消去![]() ,得
,得![]() ,
,
∴PQ中点M的轨迹方程为![]() 。。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。。7分
[解法二]由![]() ,
,![]() ,
,![]() ,得
,得
![]() 。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。5分
则![]() , ∴
, ∴![]() ,
,
将上式代入②并整理,得,![]()
∴PQ中点M的轨迹方程为![]() 。。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。。7分
(2)设直线![]() ,依题意
,依题意![]() ,则
,则![]() 。
。
分别过P、Q作![]() 轴,
轴,![]() 轴,垂足分别为P'、Q',则
轴,垂足分别为P'、Q',则
![]()
![]() 。
。
由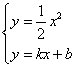 消去x,得
消去x,得![]() ③。。。。。。。。。。。。。。。。。。。。。11分
③。。。。。。。。。。。。。。。。。。。。。11分
[解法一] ∴![]()
![]()
![]() ≥
≥![]()
![]() =
=![]()
![]()
![]() 。
。
∵y1、y2可取一切不相等的正数,
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。 15分
).。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。 15分
[解法二]∴![]() =
=![]()
![]() =
=![]()
![]() 。
。
当b>0时,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() >
>![]() ;
;
当b<0时,![]()
![]()
![]()
![]() 。
。
又由方程③有两个相异实根,得△![]() ,
,
于是![]() ,即
,即![]() 。
。
∴![]()
![]() 。
。
∵当![]() 时,
时,![]() 可取一切正数,
可取一切正数,
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).
).
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15分
).。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15分
22.(解:(Ⅰ)由![]() ,
,![]() ,
,![]() ,得
,得![]() .………1分
.………1分
由![]() ,得
,得![]() .……………………………………………………………2分
.……………………………………………………………2分
由![]() 只有一解,即
只有一解,即![]() ,也就是
,也就是![]() 只有一解,
只有一解,
∴![]()
∴![]() .…………………………………………………………………………………4分
.…………………………………………………………………………………4分
∴![]() .故
.故![]() .……………………………………………………………5分
.……………………………………………………………5分
(Ⅱ)∵![]() ,
,![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,……………………………6分
,……………………………6分
猜想,![]() .……………………………………………………………7分
.……………………………………………………………7分
下面用数学归纳法证明:
10 当n=1时,左边=![]() ,右边=
,右边=![]() ,∴命题成立. ……………………8分
,∴命题成立. ……………………8分
20 假设n=k时,命题成立,即![]() ;当 n=k+1时,
;当 n=k+1时,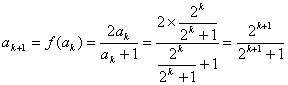 ,
,
∴当 n=k+1时,命题成立. ……………………………………………………………10分
由10,20可得,当![]() 时,有
时,有![]() .∵
.∵![]() ,∴
,∴![]()
∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,其通项公式为
的等比数列,其通项公式为![]() .……………11分
.……………11分
(Ⅲ)∵![]() ,
,
∴![]() …………………………13分
…………………………13分
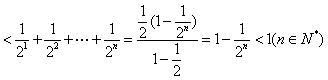 .………………………………15分
.………………………………15分
温八中 刘洪钊