08届高三数学(文)上期期中考试卷
本试卷分第I卷(选择题共60分)和第II卷(非选择题共90分)两部分。考试时间为120分钟,满分为150分。
第Ⅰ卷(选择题 共60分)
一、选择题(本题共12个小题,每题5分,共60分)
1.已知集合![]() ,则
,则![]() ( )
( )
|
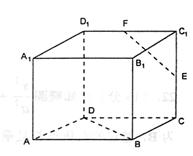
2.如右图,正方体ABCD—A1B1C1D1中,E、F分别是
CC1、C1D1的中点,则异面直线EF和BD所成的角
的大小为 ( )
A.75° B.60°
C.45° D.30°
3.一个工厂生产了某种产品24000件,它们来自甲、乙、丙3条生产线,现采用分层抽样的方法对这批产品进行抽样检查。已知从甲、乙、丙3条生产线依次抽取的个体数恰好组成一个等差数列,则这批产品中乙生产线的生产的产品数量是YCY ( )
A.12000 B.6000 C.4000 D.8000
4.若圆![]() 和圆
和圆![]() 关于
关于![]() 对称,过点
对称,过点![]() 的圆P与y轴相切,则圆心P的轨迹方程是 ( )
的圆P与y轴相切,则圆心P的轨迹方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.将函数y=4x+3的图象按向量a平移到y=4x+16的图象,则向量a可以为 ( )
A.(3,1) B.(-3,-1) C.(3,-1) D.(-3,1)
6.函数![]() 在
在![]() 上最大值等于 ( )
上最大值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设![]() 则
则![]()
( )
A.127 B.128 C.0 D.-127
8.某电视台邀请了6位同学的父母共12人,请这12位家长中的4位介绍教育子女的情况,那么这4位中至多一对夫妻的选择方法为 ( )
A.15种 B.120种 C.240种 D.480种
9.已知当![]() 时,函数
时,函数![]() 满足
满足![]() 且
且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.三个实数a、b、c成等比数列,若a+b+c=1成立,则b取值范围是 ( )
A.[0,![]() ] B.[-1,
] B.[-1,![]() ] C.[-
] C.[-![]() ,0] D.[1,0]
,0] D.[1,0]![]() (0,
(0,![]() ]
]
11. 双曲线![]() 的左右顶点分别为
的左右顶点分别为![]() 为其右支上一点,且∠A1PA2=
为其右支上一点,且∠A1PA2=
4∠PA1A2。则∠PA1A2等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
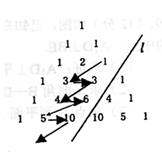
1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于 ( )
A.129 B.172
C.228 D.283
第II卷(非选择题 共90分)
二、填空题(本题共4个小题,每题4分,共16分)
|
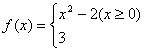 ,则
,则14.函数![]() 的单调递增区间为
。
的单调递增区间为
。
15.平面上三点A、B、C满足![]() ,
,![]() ,则
,则![]() +
+
![]() .
.
16.如果三棱锥的三个侧面两两垂直,它们面积分别为6cm2、4cm2、3cm2,那么它的外接球体积是 。
三、解答题(本大题分6小题,共74分。解答应写出文字说明、证明程或演算步骤)
17.(12分)已知![]() 且
且![]() 解关于x的不等式:
解关于x的不等式:
![]() >a+2
>a+2
18.(12分)甲、乙两支中学生足球队,苦战90分钟,比分2:2,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员点球命中概率均为0.5。
(1)两队球员一个间隔一个出场射球,有多少种不同的出场顺序?
(2)不考虑乙球队,甲球队五名队员有连续两个队员射中,英才苑且其余队员均未射中,概率是多少?
(3)甲乙两队各射完5个点球后,再次出现平局的概率是多少?
|
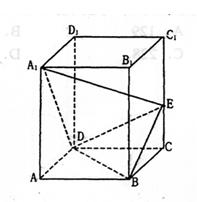
(1)求证:A1D⊥平面BDE;
(2)求二面角B—DE—C的大小;
(3)求点B到平面A1DE的距离。
20.(12分)△ABC中,内角A、B、C的对边分别为a、b、c已知a、b、c成等比数例,且![]()
(1)求![]() 的值;
的值;
(2)设![]() =,求a+c的值。
=,求a+c的值。
21.(13分)已知数列![]() 满足:
满足: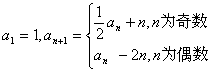
(1)求a2 , a3 , a4 , a5 ;
(2)设![]() ,求证
,求证![]() 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(3)在(2)条件下,求数列![]() 前100项中的所有偶数项的和S。
前100项中的所有偶数项的和S。
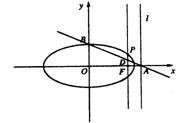
22.(13分)已知椭圆![]() (a>b>0),其右准线l与x轴交于点A,英才苑椭圆的上顶点为B,过它的右焦点F且垂直于长轴的直线交椭圆于点P,直线AB恰好经过线段FP的中点D。
(a>b>0),其右准线l与x轴交于点A,英才苑椭圆的上顶点为B,过它的右焦点F且垂直于长轴的直线交椭圆于点P,直线AB恰好经过线段FP的中点D。
(1)求椭圆的离心率;
(2)设椭圆的左、右顶点分别是A1、A2,且![]() ,求椭圆方程;
,求椭圆方程;
(3)在(2)的条件下,设Q的椭圆右准线l上异于A的任意一点,直线QA1、QA2与椭圆的另一个交点分别为M、N,求证:直线MN与x轴交于定点。
|
参考答案
一、选择题
1—6 DBDCDD 7—12 ADCDCD
二、填空题
13.3 14.![]() 15.-25 16.
15.-25 16.![]()
三、解答题
17.(满分12分)
解:![]() ∴
∴![]() 则
则![]() …………3分
…………3分
![]() ∴不等式
∴不等式![]() >a+2 ∵a<0 ∴
>a+2 ∵a<0 ∴![]() <
<![]() 即
即![]() <1+
<1+![]() ……5分
……5分
①当![]() 时,
时,![]() <0,不等式无解
<0,不等式无解
②当![]() 时,
时,![]() <0无解
<0无解
③
当![]() <
<![]() 时,
时,![]() <
<![]() <
<![]() <
<![]() <
<![]()
∴![]() <x<
<x<![]()
![]() <x
<x![]() …………10分
…………10分
综上所述,原不等式的解集为:
①当![]() 时,不等式无解
时,不等式无解
②当![]() 时,不等式解集为
时,不等式解集为
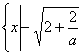 <x<
<x<![]() 或
或![]() <x<
<x<![]() …………12分
…………12分
18.(满分12分)
(1)甲乙两队各五名球员,一个间隔一个排序,出场序的种数是![]() ……3分
……3分
(2)甲队五名球员,取连续两名的方法数为4。若不考虑乙队,甲队有具只有连续两名队员射中的概率为![]() …………………7分
…………………7分
(3)甲、乙两队点球罚完,再次出现平局,可能的情况以下6种,即均未中球,均中1球,…均中5球,故所求概率为![]()
![]() …………………12分
…………………12分
19.(1)∵AA1⊥面ABCD, ∴AA1⊥BD,
又BD⊥AD, ∴BD⊥A1D …………………2分
又A1D⊥BE,∴A1D⊥平面BDE …………………3分
(2)连B1C,则B1C⊥BE,易证Rt△CBE∽Rt△CBB1,
∴![]() ,又E为CC1中点,∴
,又E为CC1中点,∴![]()
∴![]() ……………………5分
……………………5分
取CD中点M,连BM,则BM⊥平面CD1,作MN⊥DE于N,连NB,则∠BNM是二面角B—DE—C的平面角 ……………………7分
Rt△CED中,易求得MN=![]() 中,
中,![]() ∠BNM=
∠BNM=![]()
∴∠BNM=arctan![]() …………………10分
…………………10分
(3)易证BN长就是点B到平面A1DE的距离 …………………11分
∴∠BN= ![]() …………………12分
…………………12分
20.(满分12分)
解:(Ⅰ)由
![]() 得
得![]() 。
…………………2分
。
…………………2分
由b2=ac及正弦定理得sin2B=sin A sin C.
于是 cot A +
cot C =![]()
=![]()
=![]()
=![]()
=![]()
![]()
=![]()
=![]() …………………7分
…………………7分
![]()
![]() (Ⅱ)由 · =
(Ⅱ)由 · =![]() ,得
,得![]() ,又由
,又由![]() ,可得
,可得![]() ,即
,即![]() 。
。
由余弦定理![]()
![]() …………………9分
…………………9分
![]()
所以
![]() …………………12分
…………………12分
21.(满分13分)
解:(Ⅰ)
![]() …………………4分
…………………4分
(Ⅱ)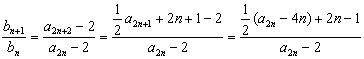 …………………6分
…………………6分
=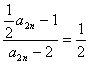 …………………8分
…………………8分
![]() …………………9分
…………………9分
∴数列![]() 是等比数列,且
是等比数列,且 ![]() …………………10分
…………………10分
(Ⅲ)由(Ⅱ)得:![]() …………………11分
…………………11分
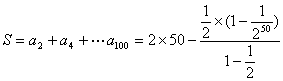 ………………12分
………………12分
![]() ………………13分
………………13分
22.(满分13分)
解:(Ⅰ)∵椭圆方程为![]() (a>b>0,c>0,c2=a2-b2)
(a>b>0,c>0,c2=a2-b2)
∴![]() ,FP的中点D的坐标为(
,FP的中点D的坐标为(![]() )……2分
)……2分
直线AB的方程为: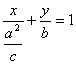 ∵D在直线AB上∴
∵D在直线AB上∴![]() ……3分
……3分
化简得![]() ∴
∴![]() …………………4分
…………………4分
(Ⅱ)![]() …………5分
…………5分
![]() =-3 ∴
=-3 ∴![]() …………………6分
…………………6分
由(Ⅰ)得:![]() …………………7分
…………………7分
∴![]()
∴椭圆方程为:![]() …………………8分
…………………8分
(Ⅲ)设直线QA1和QA2斜率分别为k1、k2,则
由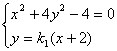
![]()
解得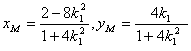 ……10分由
……10分由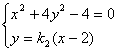
![]() 解得
解得![]()
![]() 直线MN的方程为
直线MN的方程为![]() 令y=0
令y=0
得![]() 化简得
化简得![]()
∵![]() ∴
∴![]() ∴
∴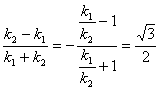
∴![]() 即直线MN与x轴交于定点(
即直线MN与x轴交于定点(![]() ) ……………13分
) ……………13分