高三文科数学下学期第五次月考试卷
数学（文）试卷
命题人：阳志长 审题人：赵家早
本卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分
考生注意事项：
1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间120分钟。
2. 答题前，考生务必将密封线内项目和座次号填写清楚。
3. 请将第Ⅰ卷各题的答案填在答题卷上，考试只交答题卷。
4. 只能用黑色签字笔答题。
5. 答题时不要将答案写在密封线内。
第 I 卷
一．选择题 （每小题5分，共50分）
1. 已知
、
均为单位向量，它们的夹角为60°，那么
=
A．
B．
C．
D．
2. 函数
的最小正周期为
A. 
B.
C.
D. 2
3. 已知向量
,向量
则
的最大值是
A．
B．
C．16 D．4
4. 
5. 已知
为非零的平面向量. 甲：
A.甲是乙的充分条件但不是必要条 B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件 D.甲既不是乙的充分条件也不是乙的必要条件
6. 在△ABC中，三边
成等差数列，
也成等差数列，则△ABC是
A.正三角形 B.等腰三角形 C.直角三角形 D.钝角三角形
7. 若
则
A.
B.
C.
D.
8.
的值是
9. 函数 
的图像按向量 
平移后, 得到的图像的解析式为
.那么 的解析式为
A.
B.
C.
D.
10.设
，
为坐标原点，若
方向上的投影相同，则
与
满足的关系式为
A.
B. 
C. 
D. 
第Ⅱ卷（非选择题 共5道填空题6道解答题）
二.填空题 （每小题5分，共25分）
11. 在平行四边形中有一点，使得从它向各顶点所引的向量之和等于零向量，
则这个点应是_________
12. 已知△ABC中，角A、B、C所对的边分别为a，b，c。若a=1，∠B=45°，
△ABC的面积S=2，那么△ABC的外接圆的直径等于________________。
13. 
14. 
写出一个与以上两式规律相同的一个等式： .
15.正整数按下表排列：
1 2 5 10 17 …
4 3 6 11 18 …
9 8 7 12 19 …
16 15 14 13 20 …
25 24 23 22 21 …
… … … … … …
位于对角线位置的正整数1,3，7,13,21，…，构成数列
，则
通项公式
三.解答题 （共75分）
16(12分).已知
的值。
17(12分). 已知：函数
的图象在原点附近最高点为A(1,2)，且图象过点B
。
(Ⅰ)求函数
的解析式；
(Ⅱ)求函数
的最大值与最小值。
18(12分). 甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0.4，每场比赛均要分出胜负，比赛时采用三场两胜制，即先取得两场胜利的球队胜出。
(Ⅰ)求甲队以二比一获胜的概率；
(Ⅱ求乙队获胜的概率；
(Ⅲ)若比赛采用五场三胜制，试问甲获胜的概率是增大还是减小，请说明理由。
19(13分). 
(Ⅰ)试用x表示；
(Ⅱ) 的最大值，并求此时
的夹角的大小.
20(13分). 
(Ⅰ)
(Ⅱ)
21(13分).已知数列的前项和
，且
，其中
为正常数，且
。
(Ⅰ) 数列
的通项公式；
(Ⅱ)当
时，设
的图象在
轴上截得的线段长为
，求
。
参考答案（仅供参考）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | C | D | B | B | A | C | C | B | A |
6. 由题设，
且
, ∴
,
∴
, 即 
, 从而
, ∴
.
9. 
, 即 .故选 B．
二.填空题答案:
11. 对角线交点 12. 
13. 30°
14. sin210°+cos240°+sin10°cos40°=3/4 (答案不唯一) 15. 43，
三.解答题答案:
16. 解：
，
------3分
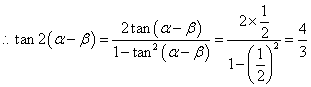。---------6分
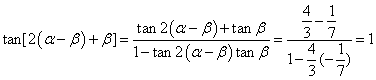。---12分
17. 解：（Ⅰ）由题意A=2，周期T=8。
-------3分
又图象过点B
，
，
，
。---------6分
（Ⅱ）
----7分
=
，---10分
故函数的最大值是
，最小值是
。------12分
18. 解：（Ⅰ）甲队以二比一获胜，即前两场中甲胜1场，第三场甲获胜，其概率为
。-------4分
（Ⅱ）乙队以2：0获胜的概率为
------5分
乙队以2：1获胜的概率为
-----6分
乙队获胜的概率为
。----8分
(Ⅲ)若三场两胜，则甲获胜的概率为
------9分
或
。
若五场三胜，则甲获胜的概率为
。-----11分
，比赛采用五场三胜制，甲获胜的概率将增大。----12分
19. 解：(Ⅰ) 
。---------4分
(Ⅱ)
-----5分
令f '(x)=0，得x=1或x= -2，当x∈［-4，-2］时， f '(x)＞0，f(x)为增函数；
f(x)有最大值：f(-2)=10.--------9分
∴当x=-2时，a·b取最大值为10.-----10分
此时，a =(-2，-6)，b=(4，-3)，｜a｜=
，｜b｜=5，-----11分
设夹角为θ，
------13分
20. 解：
，----2分
，
.---------4分
.------6分
(Ⅱ)
------------8分
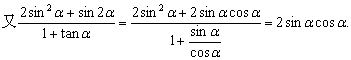------10分
------13分
21.解：(Ⅰ) 
(1)
(2)--------2分
(1)-(2)得
，即
----4分
，当
时，
，得
，-----5分
数列是以为首项，为公比的等比数列，
-----6分
(Ⅱ)由(Ⅰ)得
=
。
，由
，-------8分
，-----10分
于是
=
。-----13分