高三理科数学上学期质量检测

高三理科数学上学期质量检测

数学试题（理科）

一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的，将正确选项的字母填在答题卡相应的表格中.）

1．若不等式成立的充分条件是则实数a的取值范围是　　　　　 （　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　　 D．

2．已知集合，则b应满足

　 的条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　B．　　　 C．　 D．

3．如果成等比数列，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　 B．　 C．　 D．

4．若函数上是增函数，则实数的取值范围是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　B．[－2，1]　　　　　　 C．　　　　　　　 D．（－2，1）

5．已知等差数列{an}的前n项和为S_n，若且A、B、C三点共线（该直线不过点O），则S₂₀=　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．10　　　　　　　　　　　B．11　　　　　　　　　　　 C．20　　　　　　　　　　　D．21

6．已知函数的反函数为 的最小值是　　　　　　　　　　（　　）

　　　 A．6　　　　　　　　　　　　B．7　　　　　　　　　　　　C．8　　　　　　　　　　　　D．9

7．已知△ABC的三个内角A、B、C所对的三边分别为a、b、c，若△ABC的面积，则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．4

8．过点M（3，0）的直线交⊙于A、B两点，C为圆心，则 的最小值是　　　　　　　　 　　（　　）

　　　 A．8　　　　　　　　　　　　B．6　　　　　　　　　　　　C．　　　　　　　　　　D．4

9．如图，在长方体ABCD—A₁B₁C₁D₁中，M、N分别

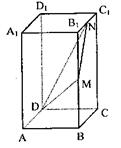
为BB₁、B₁C₁的中点，P为平面DMN内的一动点，

若点P到平面BCC₁B₁的距离等于PD时，则点的轨

迹是　　　　　　　　　　　　　　  （　　）

　　　 A．圆或圆的一部分

　　　 B．抛物线的一部分

　　　 C．双曲线的一部分

　　　 D．椭圆的一部分

1,3,5

10．设定义域为R的函数都有反函数，并且函数的图像关于直线的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1005　　　　　　　　　 B．2008　　　　　　　　　 C．1003　　　　　　　　　 D．以上结果均不对

1,3,5

第Ⅱ卷（非选择题，共100分）

二、填空题（本大题共5小题，每小题5分，共25分，将答案写在答题卡相应的横线上.）

11．在三棱锥P—ABC中，PA、PB、PC两两互相垂直，且PA=PB=PC=2，则三棱锥P—ABC的外接球的球面面积是　　　　　　  .

12．设数列是等差数列，T_n、S_n分别是数列的前n项和，且 则　　　　　　  .

13．给出下列命题：

①函数内单调递增；

②函数的最小正周期为；

③函数的图形是关于直线成轴对称的图形；

④函数的图形是关于点成中心对称的图形.

其中正确命题有　　　　　　  .

14．设F为抛物线A、B、C为该抛物线上三点，若，则=　　　　　　  .

15．已知A（3，），O为原点，点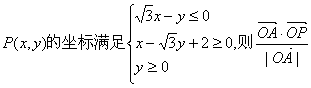的最大值是　　　　　　  ，此时点P的坐标是　　　　　　  .

三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程和演算步骤，将答案写在答题卡相应处.）

16．（本小题满分12分）已知关于x的不等式 的解集分别为A和B，且，求实数a的取值范围.

17．（本小题满分12分）已知平面向量向量

　 （1）求证：；

　 （2）令.

18．（本小题满分12分）如图，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，AD=2，AB=2F、G分别是AB、AD的中点.

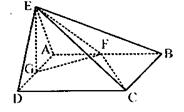
　 （1）求证：CF⊥平面EFG；

　 （2）若P为线段CE上一点，且

求DP与平面EFG所成的角.

19．（本小题满分12分）设数列的各项都是正数，对任意 为数列的前n项和.

　 （1）求数列的通项公式；

　 （2）设（为非零整数，），试确定的值，使得对任意都有成立.

20．（本小题满分13分）有如下结论：“圆上一点处的切线方程为”，类比也有结论：“椭圆处的切线方程为”，过椭圆C：的右准线l上任意一点M引椭圆C的两条切线，切点为 A、B.

　 （1）求证：直线AB恒过一定点；

　 （2）当点M在的纵坐标为1时，求△ABM的面积.

21．（本小题满分14分）已知函数的方程的两个不等实根.

　 （1）若的取值范围；

　 （2）若的最小值为

的最大值.

参考答案

一、选择题

1,3,5

1—10 ADBBA  DBBDA

二、填空题

11．12　　12．　　13．②④　 14．12　 15．

三、解答题

16．解：∵

∴

　①…………5分

又∵

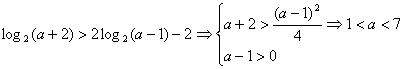∴②…………10分

由①②知，即a的取值集合M=[2，3].……………………12分

17．解：（1）∵

∴.……………………2分

　 （2）易知

∵

∴…………………………4分

即

∴

………………9分

∵

∴……………………12分

18．解：（1）∵平面EAD⊥平面ABCD，EG⊥AD，

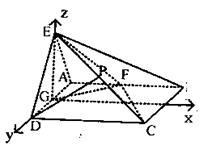
∴EG⊥平面ABCD，且EG=

以GE为z轴、AD为y轴建立如图所示

空间直角坐标系，

则E（0，0，），D（0，1，0），

C（2，1，0），F（，－1，0）.

∴

∴CF⊥FG，CF⊥EF，则CF⊥平面EFG.……………………6分

（2）∵

∴……………………8分

由（1）知=为平面EFG的一个法向量，

∵

∴……………………10分

∴DP与平面EFG所成的角为……………………12分

19．解：（1）∵由已知，当n=1时，

∴………………………………1分

∵　①

∴当　②

①—②得

∵

∴…………………………3分

因此，数列是首项为1，公差为1的等差数列，故得………………4分

　 （2）

要使恒成立

即使

恒成立，

即恒成立.

当n为偶数时，即为恒成立，又

∴…………………………………………9分

当n为奇数时，即为恒成立，又

∴……………………………………………………………………11分

∴

∴

∴，使得任何……………………12分

20．解：（1）设M

………………1分

∵点M在MA上

∴　①……………………3分

同理可得②…………………………5分

由①②知AB的方程为…………7分

易知右焦点F（）满足③式，故AB恒过椭圆C的右焦点F（）……9分

（2）把AB的方程

∴……………………11分

又M到AB的距离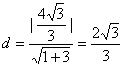

∴△ABM的面积……………………13分

21．解：（1）∵①……2分

又

∴同号.……………………3分

当

∵

∴

∴

∴

代入①式得……………………6分

当

∵

∴

∴

∴代入①式得

∴b的取值范围为……………………8分

（2）

…………10分

∵

对称轴为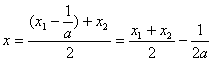

且…………12分

∴

易知上单调递减，

∴的最大值为

时取得.…………………………14分