高三数学上学期期末试卷
时量:120分钟 满分:150分
一、选择题(每小题5分,共60分)
1.已知全集![]() 等于( )
等于( )
A.{1,4} B.{2,6} C.{3,5} D.{2,3,5,6}
2.已知![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(理)若纯虚数z满足![]() ,则实数b等于( )
,则实数b等于( )
A.2 B.8 C。-2 D.-8
(文)从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm的概率为( )
A.0.2 B.0.3 C.0.7 D.0.8
4.函数![]() 为奇函数且周期为3,
为奇函数且周期为3,![]() 等于 ( )
等于 ( )
 A.0 B.1 C.-1 D.2
A.0 B.1 C.-1 D.2
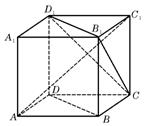
5.如图,![]() 为正方体,下面结论错误的是( )
为正方体,下面结论错误的是( )
(A)![]() 平面
平面![]() (B)
(B)![]()
(C)![]() 平面
平面![]() (D)异面直线
(D)异面直线![]() 与
与![]() 所成的角为60°
所成的角为60°
6.将直线![]() 沿
沿![]() 轴向左平移1个单位,所得直线与圆
轴向左平移1个单位,所得直线与圆![]() 相切,则实数
相切,则实数![]() 的值为( )
的值为( )
A.-3或7 B.-2或8 C.0或10 D.1或11
7.数列{![]() }的前n项和为 ( )
}的前n项和为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.直线![]() 与
与![]() 垂直,则
垂直,则![]() 等于
等于
A.![]() B.
B.![]() C.-1 D.2或-1
C.-1 D.2或-1
9、若![]() ∈R+,且
∈R+,且![]() +
+![]() =1,则
=1,则![]() 的最小值是( )
的最小值是( )
A.16 B.12 C.10 D.8
10.(理)曲线![]() 上的点到直线
上的点到直线![]() 的最短距离是( )
的最短距离是( )
A.0 B.![]() YCY C.
YCY C.![]() D.
D.![]()
(文)过函数![]() 图象上一点P(1,-3)的切线的倾斜角为( )
图象上一点P(1,-3)的切线的倾斜角为( )
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() ;
;
11.某科技小组有6名同学,现从中选出3人去参观展览,若至少有1名女生入选时的不同选法有16种,则小组中的女生数目为 ( )
A.2 B.3 C.4 D.5
12.已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() ,若
,若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是(
)
的等差中项,则椭圆的离心率是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,共16分)
13.函数![]() 的定义域是
.
的定义域是
.
14.在等比数列{an}中,a3=3,前3项和S3=9,则公比q=
15.已知实数![]() 满足不等式组
满足不等式组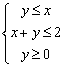 ,那么函数
,那么函数![]() 的最大值是
.
的最大值是
.
16.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直线坐标系中,利用求动点轨迹方程的方法,可以求出过点![]() ,且法向量为
,且法向量为![]() 的直线(点法式)方程为
的直线(点法式)方程为![]() ,化简得
,化简得![]() . 类比以上方法,在空间直角坐标系中,经过点
. 类比以上方法,在空间直角坐标系中,经过点![]() 且法向量为
且法向量为![]() 的平面(点法式)方程为 .(请写出化简后的结果)
的平面(点法式)方程为 .(请写出化简后的结果)
三.解答题(共74分)
17.(12分)已知![]() ,
,![]() .
.
①求![]() 的值; ②求
的值; ②求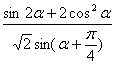 的值.
的值.
18、(12分)数列![]() 的前n项和为Sn,且a1=2,
的前n项和为Sn,且a1=2,![]()
①求数列![]() 的通项公式;
的通项公式;
②等差数列![]() 的各项为正,其前n项和为Tn,且T3=30,
的各项为正,其前n项和为Tn,且T3=30,
又![]() 成等比数列,求Tn.
成等比数列,求Tn.
19.(12分)(理)某地最近出台一项机动车驾照考试规定;每位考试者一年之内
最多有4次参加考试的机会,一旦某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。李明决定参加驾照考试,设他每次参加考试通过的概率依次
为0.6,0.7,0.8,0.9。
(1)求在一年内李明参加驾照考试次数![]() 的分布列和
的分布列和![]() 的期望。
的期望。
(2)求李明在一年内领到驾照的概率.
(文)甲、乙、丙3人投篮,投进的概率分别是, , .现3人各投篮1次,
是否命中相互之间不受影响,求:
(1) 3人都投进的概率;
(2) 3人中恰有2人投进的概率.
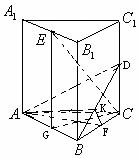
20.(12分)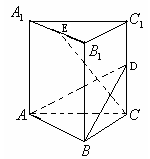 如图所示,在正三棱柱
如图所示,在正三棱柱![]() 中,底面边长和侧棱都是2,D是
中,底面边长和侧棱都是2,D是![]() 的中点.E是
的中点.E是![]() 的中点.
的中点.
(1)求证:![]() 平面DAB;
平面DAB;
(2)求证:![]() ;
;
(3)求二面角A—DB—C的平面角的正切值.
21.(12分)设函数![]() 是定义在R上的奇函数,且函数
是定义在R上的奇函数,且函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)(理)若对任意![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(文)若对任意![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
22.(14分)已知:定点F(1,0),动点P在y轴上移动,过点P作直线PM交x轴于点M,并延长MP到N,且![]()
(1)求点N轨迹方程;
(2)直线![]() 与点N的轨迹交于不同的两点A、B,若
与点N的轨迹交于不同的两点A、B,若![]() ,O为坐标原点,且
,O为坐标原点,且![]() ,求m的取值范围.
,求m的取值范围.
参考解答
一. CABBD ACAAD AD
二.
13。![]() 14。1或
14。1或![]() 15。4 16。
15。4 16。![]()
三.
17。解:①由![]() (4分)
(4分)
②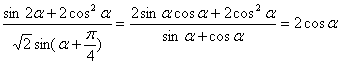 (8分)
(8分)
![]() ,且
,且![]() 原式=
原式=![]() (12分)
(12分)
18.解:①![]() 当
当![]() 时,
时,![]()
两式相减![]() (3分)
(3分)
又![]()
![]() 是以
是以![]() ,
,
公比为3的等比数列 ![]() (6分)
(6分)
②由(1)![]() ,设
,设![]() 的公差为d
的公差为d![]()
又T3=30 ![]() (8分)
(8分)
![]()
![]()
由题意![]()
又![]() 的各项为正
的各项为正![]() (10分)
(10分)
![]() (12分)
(12分)
19。(理)解:(1)![]() 的取值分别为1,2,3,4.
的取值分别为1,2,3,4.
![]() ,表明李明第一次参加驾照考试就通过了,故P(
,表明李明第一次参加驾照考试就通过了,故P(![]() )=0.6.
)=0.6.
![]() ,表明李明在第一次考试未通过,第二次通过了,故
,表明李明在第一次考试未通过,第二次通过了,故
![]()
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
![]()
ξ=4,表明李明第一、二、三次考试都未通过,故
![]()
∴李明实际参加考试次数ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | 0.6 | 0.28 | 0.096 | 0.024 |
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544.
(2)李明在一年内领到驾照的概率为
P=1-(1-0.6)(1-0.7)(1-0.8)(1-0.9)=0.9976.
(文).解: (1)记"甲投进"为事件A1 , "乙投进"为事件A2 , "丙投进"为事件A3,
则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A1A2A3)=P(A1) ·P(A2) ·P(A3)
= × ×![]() =
= ![]()
∴3人都投进的概率为![]() ………………6分
………………6分
(2) 设“3人中恰有2人投进"为事件B
P(B)=P(A2A3)+P(A1A3)+P(A1A2)
=P()·P(A2)·P(A3)+P(A1)·P()·P(A3)+P(A1)·P(A2)·P()
=(1-)× ×![]() + ×(1-)×
+ ×(1-)×![]() + × ×(1-
+ × ×(1-![]() ) =
) = ![]()
∴3人中恰有2人投进的概率为![]() ………………12分
………………12分
20.解:(1)证明:由正三棱柱的性质知![]() ,
,
因为![]() 平面ABD,
平面ABD,![]() 平面ABD,所以
平面ABD,所以![]() 平面DAB ……3分
平面DAB ……3分
(2)解:设AB中点为G,连![]() ,则
,则![]() ,且
,且![]() ,
,
所以![]() ,而
,而![]() 平面EGC
平面EGC
所以![]() (或用三垂线定理也可)……6分
(或用三垂线定理也可)……6分
(3)解:设F是BC的中点,则![]()
又![]() 平面ABC,所以
平面ABC,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
作![]() 于K,连AK,由三垂线定理知
于K,连AK,由三垂线定理知![]() ,
,
故![]() 是二面角A—BD—C的平面角,在
是二面角A—BD—C的平面角,在![]() 中,
中,![]()
![]()
所以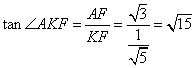
即二面角A—DB—C的平面角的正切值为![]() .……12分
.……12分
(说明:向量方法解同样给分)
21.解:(Ⅰ)∵ 函数![]() 是定义在R上的奇函数,
是定义在R上的奇函数,
∴ ![]() ∵
∵ ![]()
∴ ![]() . 又
. 又![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
由![]() ∴
∴ ![]() ,且
,且![]() ,
,
∴ ![]() 得
得![]()
(Ⅱ)(理)解:![]() ,即
,即![]()
∴ 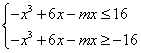 即
即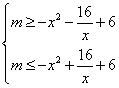 对任意
对任意![]() 恒成立,
恒成立,
记![]() ,其中
,其中![]() 则
则 ![]()
∴ 当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
∴ ![]() 在
在![]() 上的最大值是
上的最大值是![]() ,则
,则![]() ;
;
记![]() ,其中
,其中![]() 则
则 ![]()
所以 ![]() 在
在![]() 上单调递减,
上单调递减,
∴ 即![]() 在
在![]() 上的最小值是
上的最小值是![]() ,则
,则![]() ;
;
综合上可得所求实数![]() 的取值范围是
的取值范围是![]() .
.
(文)解:![]() 依题意
依题意![]() 对任意
对任意![]() 恒成立,
恒成立,
∴ ![]() 对任意
对任意![]() 恒成立,
恒成立,
即 ![]() 对任意
对任意![]() 恒成立,∴
恒成立,∴ ![]() .
.
22解:(1)设点N坐标为![]() ∵M、P、N三点共线
∵M、P、N三点共线![]()
∴![]() 又
又![]() ∴
∴![]() ,即点P
,即点P![]()
∴![]() 由
由![]()
(2)将![]() ,代入抛物线整理得:
,代入抛物线整理得:![]() 即
即![]()
则由题意:![]() 即
即![]()
由韦达定理知:![]()
又![]() 即:
即:![]()
得:![]() ,可知:
,可知:![]()
此时![]() 即
即![]()
可得:![]()
解得:![]()
所以m范围![]() …………12分
…………12分