高三第三次调研考试数学试题
第Ⅰ卷(选择题,共50分)
一.选择题:本大题共l0小题,在每小题给出的四个选项中,只有一项是符合题目要求的.每小题5分,满分50分.
1.设集合![]() ,则满足
,则满足![]() 的集合B的个数是( )。
的集合B的个数是( )。
A.1 B.3 C.4 D.8
2.如果复数![]() 为纯虚数,那么实数
为纯虚数,那么实数![]() 的值为( )。
的值为( )。
A.-2 B.1 C.2 D.1或 -2
3. 已知等差数列{an}中,a2+a8=8,则该数列前9项和S9等于( )。
 A.18 B.27
C.36 D.45
A.18 B.27
C.36 D.45
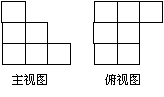
4.用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
则它的体积的最小值与最大值分别为( )。
A.![]() 与
与![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
5.若函数![]() 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1.5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
那么方程![]() 的一个近似根(精确到0.1)为( )。
的一个近似根(精确到0.1)为( )。
A.1.2 B.1.3 C.1.4 D.1.5
6.“m=![]() ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )。
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )。
A.充分必要条件 B.充分而不必要条件
C..必要而不充分条件 D.既不充分也不必要条件
7.下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )。
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()

8.定义运算a![]() b=
b=![]() ,则函数f(x)=1
,则函数f(x)=1![]() 2
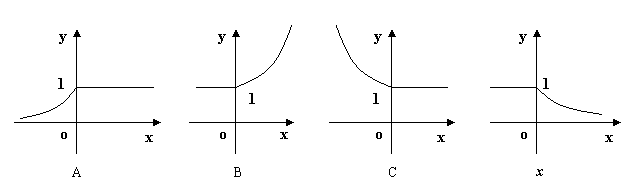
2![]() 的图象是( )。
的图象是( )。
9.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为( )。
的值为( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知定义域为(-1,1)的奇函数y=f (x)又是减函数,且f (a-3)+f (9-a2)<0,则a的取值范围是( )。
A.(2![]() ,3)
B.(3,
,3)
B.(3,![]() ) C.(2
) C.(2![]() ,4) D.(-2,3)
,4) D.(-2,3)
第Ⅱ卷(非选择题,共100分)
 二.填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
二.填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
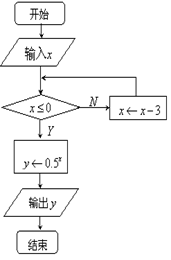
11.右面是一个算法的程序框图,当输入的值![]() 为5时,
为5时,
则其输出的结果是 .
12.下图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,
数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影
![]() 部分的面积为 .
部分的面积为 .
13.设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,
,![]() ,
,
则![]() .
.
14.(坐标系与参数方程选做题)直线![]() 被圆
被圆![]() 所截得的弦长为
.
所截得的弦长为
.
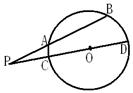 15.(几何证明选讲选做题)如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为_______________.
15.(几何证明选讲选做题)如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为_______________.
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16.(本题满分12分)
将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
17.(本题满分14分)
已知函数![]()
(I)求函数![]() 的最小正周期;
的最小正周期;
(II)求函数![]() 的值域.
的值域.
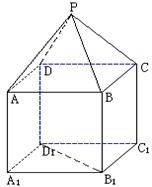 18.(本小题满分14分)
18.(本小题满分14分)
如图,P—ABCD是正四棱锥,![]() 是正方体,
是正方体,
其中![]()
![]()
(1)求证:![]() ;
;
(2)求PA与平面![]() 所成角
所成角![]() 的余弦值;
的余弦值;
19. (本小题满分14分)
数列{an}的前n项和记为Sn,![]()
(I)求{an}的通项公式;
(II)等差数列{bn}的各项为正,其前n项和为Tn,且![]() ,又
,又![]() 成等比数列,求Tn
成等比数列,求Tn
20.(本小题满分14分)
已知圆![]() :
:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
21.(本小题满分12分)
已知函数![]() 在
在![]() 是增函数,
是增函数,![]() 在(0,1)为减函数.
在(0,1)为减函数.
(I)求![]() 、
、![]() 的表达式;
的表达式;
(II)求证:当![]() 时,方程
时,方程![]() 有唯一解;
有唯一解;
(III)当![]() 时,若
时,若![]() 在
在![]() ∈
∈![]() 内恒成立,求
内恒成立,求![]() 的取值范围.
的取值范围.
高三第三次调研考试数学试题
参考答案(文科卷)
一、选择题
| 题号 |
|
|
|
|
|
|
|
|
|
|
| 答案 |
|
|
|
|
|
|
|
|
|
|
1.C解:![]() ,
,![]() ,则集合B中必含有元素3,即此题可转化为求集合
,则集合B中必含有元素3,即此题可转化为求集合![]() 的子集个数问题,所以满足题目条件的集合B共有
的子集个数问题,所以满足题目条件的集合B共有![]() 个。故选择答案C。
个。故选择答案C。
2.A 解: 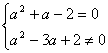 即
即 ![]() ,故选择答案A
,故选择答案A
3.C 解:在等差数列{an}中,a2+a8=8,∴ ![]() ,则该数列前9项和S9=
,则该数列前9项和S9=![]() =36,
=36,
故选择答案C
4.C 提示:由三视图可知选C
5.C 解:f(1.40625)=-0.054< 0,f(1.4375)=0.162> 0 且都接近0,由二分法可知其根近似于1.4。
6.B 解:当![]() 时两直线斜率乘积为
时两直线斜率乘积为![]() ,从而可得两直线垂直,当
,从而可得两直线垂直,当![]() 时两直线一条斜率为0,一条斜率不存在,但两直线仍然垂直.因此
时两直线一条斜率为0,一条斜率不存在,但两直线仍然垂直.因此![]() 是题目中给出的两条直线垂直的充分但不必要条件.
是题目中给出的两条直线垂直的充分但不必要条件.
7.C 解:5个有效分为84,84,86,84,87;其平均数为85。利用方差公式可得方差为1.6.
8.A 提示:信息迁移题是近几年来出现的一种新题型,主要考查学生的阅读理解能力.本题综合考查了分段函数的概念、函数的性质、函数图像,以及数学阅读理解能力和信息迁移能力.
当x<0时,2x<1, f(x) =2x; x>0时,2x>1, f(x) =1. 答案:A
9.D 解:椭圆![]() 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线![]() 的焦点为(2,0),则
的焦点为(2,0),则![]() ,故选D。
,故选D。
10.A 提示![]() 由条件得f(a-3)<f(a2-9),即
由条件得f(a-3)<f(a2-9),即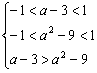 ∴a∈(2
∴a∈(2![]() ,3)
,3)![]() 故选择答案A
故选择答案A
二.填空题:
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 | 2 |
|
|
| 2 |
11.解:当x=-1时,即输出,此时![]() .
.
12.解:解利用几何概型![]() 。
。
13.解:设向量![]() 与
与![]() 的夹角为
的夹角为![]() 且
且![]() ∴
∴![]() ,则
,则![]()
 =
=![]() .
.
14. 解:把直线![]() 代入
代入
![]() 得
得![]()
![]() ,弦长为
,弦长为![]()
15. 解:设圆的半径为R,由![]() 得
得![]() 解得R=2
解得R=2
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16.解: (I) 共有![]() 种结果 ………………4分
种结果 ………………4分
(II) 若用(a,b)来表示两枚骰子向上的点数,则点数之和是3的倍数的结果有:
(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),
(3,3),(4,5),(5,4),(3,6),(6,3),(6,6)
共12种. ………………8分
(III)两枚骰子点数之和是3的倍数的概率是:P=![]() …………12分
…………12分
17.解:![]()
![]() ……………………………3分
……………………………3分
![]()
![]() ……………………………6分
……………………………6分
(I)函数![]() 的最小正周期是
的最小正周期是![]() ……………………………8分
……………………………8分
(II)∴![]() ∴
∴![]() ……………………………10分
……………………………10分
∴ ![]() …………12分
…………12分
所以![]() 的值域为:
的值域为: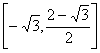 …………14分
…………14分
18、解:(1)设AC与BD交点为O,连PO;∵P—ABCD是正四棱锥,∴PO⊥面ABCD,…1分
∴AO为PA在平面ABCD上的射影, 又ABCD为正方形,∴AO⊥BD,…………3分
由三垂线定理知PA⊥BD,而BD∥B1D1;∴![]() …………………………6分
…………………………6分
(2)∵AO⊥面PBD,连PO,则∠APO为所求角;……………………………8分
可以计算得,![]() …………………………………………………………14分
…………………………………………………………14分
19.(I)由![]() 可得
可得![]() ,
………………1分
,
………………1分
两式相减得![]() ………………3分
………………3分
又![]() ∴
∴![]() ,故{an}是首项为1,公比为3得等比数列 ……4分
,故{an}是首项为1,公比为3得等比数列 ……4分
∴![]() .
………………………………………………………6分
.
………………………………………………………6分
(II)设{bn}的公差为d,由![]() 得,可得
得,可得![]() ,可得
,可得![]() , ………8分
, ………8分
故可设![]() ………………9分
………………9分
又![]() 由题意可得
由题意可得
![]() 解得
解得![]() ………………………………11分
………………………………11分
∵等差数列{bn}的各项为正,∴![]() ,∴
,∴![]() …………………………12分
…………………………12分
∴![]() …………………………………………………14分
…………………………………………………14分
20. 解(Ⅰ)①当直线![]() 垂直于
垂直于![]() 轴时,则此时直线方程为
轴时,则此时直线方程为![]() ,
,![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,其距离为
,其距离为![]() ,满足题意…………………… 2分
,满足题意…………………… 2分
②若直线![]() 不垂直于
不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,
,
即![]() …………………………………………………… 3分
…………………………………………………… 3分
设圆心到此直线的距离为![]() ,则
,则![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
故所求直线方程为![]() ……………………………………5分
……………………………………5分
综上所述,所求直线为![]() 或
或![]() …………………… 6分
…………………… 6分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,
,![]() 点坐标为
点坐标为![]()
则![]() 点坐标是
点坐标是![]() …………………… 7分
…………………… 7分
∵![]() ,
,
∴![]() 即
即![]() ,
,![]()
![]() ……………………9分
……………………9分
又∵![]() ,∴
,∴![]() …………………………… 10分
…………………………… 10分
由已知,直线m //ox轴,所以,![]() ,…………………………… 11分
,…………………………… 11分
∴![]() 点的轨迹方程是
点的轨迹方程是![]() ,…………………… 12分
,…………………… 12分
轨迹是焦点坐标为![]() ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉![]() 两点。…………………… 14分
两点。…………………… 14分
21.解: (I)![]() 依题意
依题意![]() ,即
,即![]() ,
,![]() .
.
∵上式恒成立,∴![]() ①
…………………………1分
①
…………………………1分
又![]() ,依题意
,依题意![]() ,即
,即![]() ,
,![]() .
.
∵上式恒成立,∴![]() ②
…………………………2分
②
…………………………2分
由①②得![]() .
…………………………3分
.
…………………………3分
∴![]() …………………………4分
…………………………4分
(II)由(1)可知,方程![]() ,
,![]()
设![]() ,
,![]()
令![]() ,并由
,并由![]() 得
得![]() 解知
解知![]() ……………………5分
……………………5分
令![]() 由
由![]() …………………………6分
…………………………6分
列表分析:
|
| (0,1) | 1 | (1,+¥) |
|
| - | 0 | + |
|
| 递减 | 0 | 递增 |
知![]() 在
在![]() 处有一个最小值0,
…………………………7分
处有一个最小值0,
…………………………7分
当![]() 时,
时,![]() >0,
>0,
∴![]() 在(0,+¥)上只有一个解.
在(0,+¥)上只有一个解.
即当x>0时,方程![]() 有唯一解.
…………………………8分
有唯一解.
…………………………8分
(III)设![]() , ……………………9分
, ……………………9分
![]() 在
在![]() 为减函数
为减函数![]() 又
又![]() ……………11分
……………11分
所以:![]() 为所求范围.
…………………………12分
为所求范围.
…………………………12分