08届高三(理科)数学摸底测试试题
第一部分 选择题 (共40分)
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1. 复数![]() 的虚部为( )
的虚部为( )
![]() . 4
. 4 ![]() .—4
.—4 ![]() .
. ![]()
![]() .
. ![]()
2.
设集合![]() ,
,![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
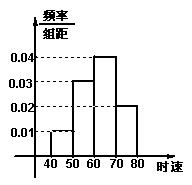 3. 若曲线
3. 若曲线![]() 所围成的图形的面积为2e,则k的值为( )
所围成的图形的面积为2e,则k的值为( )
![]() . e
. e ![]() .
.![]()
![]() .1
.1 ![]() .2
.2
4. ![]() 辆汽车通过某一段公路时的时速的频率分布直方图
辆汽车通过某一段公路时的时速的频率分布直方图
如右图所示,时速在![]() 的汽车大约有
的汽车大约有
![]() .
.![]() 辆
辆 ![]() .
. ![]() 辆
辆 ![]() .
.![]() 辆
辆 ![]() .80辆
.80辆
5.已知不等式![]() ,则
,则![]() 的解集为( )
的解集为( ) ![]()
6 已知函数![]() ,则
,则![]() 的极小值为( )
的极小值为( )
A.
![]() B。
B。![]() C。
C。![]() D。
D。![]()
7.
已知函数![]() 的图象与
的图象与![]() 的图象在
的图象在![]() 轴的右侧交点按从横坐标由小到大的顺序记为
轴的右侧交点按从横坐标由小到大的顺序记为![]() ,则
,则![]() =
=
![]() .
. ![]()
![]() .
. ![]()
![]() .
.![]()
![]() .
.![]()
8. 若定义在R上的减函数![]() ,对于任意的
,对于任意的![]() ,不等式
,不等式![]() 成立.且函数
成立.且函数![]() 的图象关于点
的图象关于点![]() 对称,则当
对称,则当 ![]() 时,
时,![]() 的取值范围
的取值范围
![]() .
.![]()
![]() .
. ![]()
![]() .
.![]()
![]() .
.![]()
 第二部分 非选择题(共110分)
第二部分 非选择题(共110分)
二.填空题:每小题5分, 共30分.
9. ![]() 的离心率等于__________,与该椭圆有
的离心率等于__________,与该椭圆有
共同焦点,且一条渐近线是![]() 的双曲线方程是
的双曲线方程是
___________________.
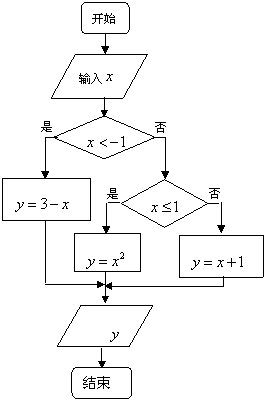
10. 运行右边算法流程,当输入x的值为_____时,输出![]() 的值为4。
的值为4。
11. 下图是一个物体的三视图,根据图中尺寸,
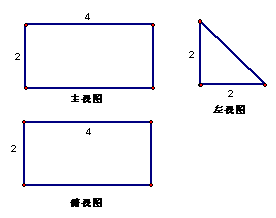 它的体积为 .
它的体积为 .
12. 设![]() 是等比数列
是等比数列![]() 的前
的前![]() 项和, 对于等比数列
项和, 对于等比数列![]() ,有命题
,有命题![]() 若
若![]() 成等差数列,则
成等差数列,则![]() 成等差数列成立;对于命题
成等差数列成立;对于命题![]() :若
:若![]() 成等差数列, 则
________________成等差数列.请将命题
成等差数列, 则
________________成等差数列.请将命题![]() 补充完整,使它也是真命题.(只要一个符合要求的答案即可)
补充完整,使它也是真命题.(只要一个符合要求的答案即可)
选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
13. 若不等式![]() 无实数解则a的取值范围是 .
无实数解则a的取值范围是 .
14.在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),若以
是参数),若以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线![]() 的极坐标方程可写为________________.
的极坐标方程可写为________________.
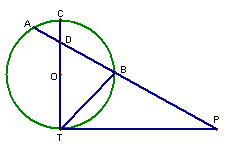 15. 已知:如图,PT切⊙O于点T,PA交⊙O于A、B两点且与直径CT交于点D,CD=2,AD=3, BD=6,则PB= .
15. 已知:如图,PT切⊙O于点T,PA交⊙O于A、B两点且与直径CT交于点D,CD=2,AD=3, BD=6,则PB= .
三、解答题:本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤.
16.(本题满分12分)
如图,在![]() 中,
中,![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ) 记![]() 的中点为
的中点为![]() ,求中线
,求中线![]() 的长.
的长.
17.(本小题满分12分)
袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的2个小球上的数字互不相同的概率;
(Ⅱ)用![]() 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量![]() 的概率分布与数学期望
的概率分布与数学期望
18. (本题满分14分)
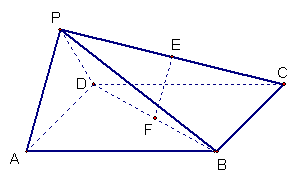 如图,在四棱锥
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
![]() 底面
底面![]() ,且
,且![]() ,若
,若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(Ⅰ) ![]() //平面
//平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 求二面角![]() 的正切值.
的正切值.
19. (本题满分14分)
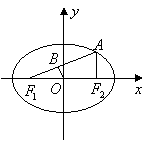
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)设![]() 为椭圆上的两个动点,
为椭圆上的两个动点,![]() ,过原点
,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
20. (本题满分14分)
已知函数![]() ,若对任意
,若对任意![]() ,
,![]() 且
且![]() ,都有
,都有![]() .
.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)对于给定的实数![]() ,有一个最小的负数
,有一个最小的负数![]() ,使得
,使得![]() 时,
时,![]() 都成立,则当
都成立,则当![]() 为何值时,
为何值时,![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
21. (本题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
08届高三(理科)数学摸底测试试题
![]() 数学(理)试题答题卷
数学(理)试题答题卷
 第二部分 非选择题答题卷
第二部分 非选择题答题卷
二、填空题(每小题5分,共30分):
9.___________,___________;10.___________;11.______________________;
12._____________________;13._____________________;
14.____________________;15._____________________
三、解答题:(共80分,要求写出解答过程)
 16.(本小题满分12分)
16.(本小题满分12分)
17.(本小题满分12分)

18.(本小题满分14分)


19.(本小题满分14分)

20.(本小题满分14分)


21.(本小题满分14分)

08届高三(理科)数学摸底测试试题答案
一、选择题答案 ABCCD ABD
二、填空题 9. ![]() ,
,![]() (第一空2分,第二空3分), 10. 3, 11. 8,
12.
(第一空2分,第二空3分), 10. 3, 11. 8,
12. ![]() 开放题,答案不唯一. 13.
开放题,答案不唯一. 13.![]() ,14.
,14. ![]() , 15. 15
, 15. 15
三、解答题
16.(本题满分12分)
解: (Ⅰ)由![]() ,
, ![]() 是三角形内角,得
是三角形内角,得![]() ……………..2分
……………..2分
∴ ![]() ………………………………………..5分
………………………………………..5分
![]() …………………………………………………………6分
…………………………………………………………6分
(Ⅱ) 在![]() 中,由正弦定理,
中,由正弦定理,![]() ,
,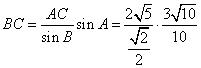
![]()
…………………………………………………………………………………………………..9分
![]() ,
, ![]() ,
,
由余弦定理得:![]()
=![]() …………………………………12分
…………………………………12分
17.(本小题满分12分)
(本小题主要考查互斥事件的概率、随机变量的分布列、数学期望等基础知识,考查分类与整合、或然与必然的数学思想与方法,以及运算求解能力)
(Ⅰ)解法一:记“取出的2个小球上的数字互不相同”为事件![]() ,
,
∵从袋中的6个小球中任取2个小球的方法共有![]() 种,
……1分
种,
……1分
其中取出的2个小球上的数字互不相同的方法有![]() ,
……3分
,
……3分
∴![]() .
……4分
.
……4分
解法二:记“取出的2个小球上的数字互不相同”的事件记为![]() ,“取出的2个小球上的数字相同”的事件记为
,“取出的2个小球上的数字相同”的事件记为![]() ,则事件
,则事件![]() 与事件
与事件![]() 是对立事件.
是对立事件.
∵![]() ,
……2分
,
……2分
∴![]() .
……4分
.
……4分
(Ⅱ)解:由题意,![]() 所有可能的取值为:2,3,4,5,6.
……6分
所有可能的取值为:2,3,4,5,6.
……6分
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
故随机变量![]() 的概率分布为
的概率分布为
|
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
……10分
因此,![]() 的数学期望
的数学期望![]() .……12分
.……12分
解: (Ⅰ)设事件![]() 表示“甲选做14题”,事件
表示“甲选做14题”,事件![]() 表示“乙选做14题”,则甲、乙2名学生选做同一道题的事件为“
表示“乙选做14题”,则甲、乙2名学生选做同一道题的事件为“![]() ”,且事件
”,且事件![]() 、
、![]() 相互独立…………………………..2分
相互独立…………………………..2分
∴ ![]() ………………………………..4分
………………………………..4分
=![]() ………………………………6分
………………………………6分
(Ⅱ)随机变量![]() 的可能取值为0,1,2,3,4.且
的可能取值为0,1,2,3,4.且![]() .
.
∴ ![]() ………………….8分
………………….8分
所以变量![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
…………………………………………………………………………………………….10分
![]() 或
或![]() …………..12分
…………..12分
18.(本题满分14分)
(Ⅰ)证明:连结![]() ,在
,在![]() 中
中![]() //
//![]() ………………………………………………………………..2分
………………………………………………………………..2分
且![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() …………………………………………………………………………………………………….4分
…………………………………………………………………………………………………….4分
(Ⅱ)证明:因为面![]()
![]() 面
面![]() 平面
平面![]()
![]() 面
面![]()
![]()
![]()
所以,![]() 平面
平面![]()
![]() ………………………………………………………………………6分
………………………………………………………………………6分
又![]() ,所以
,所以![]() 是等腰直角三角形,且
是等腰直角三角形,且![]()
即![]() …………………………………………………………………………………………………………………….8分
…………………………………………………………………………………………………………………….8分
![]() ,且
,且![]() 、
、![]()
![]() 面
面![]()
![]() 面
面![]()
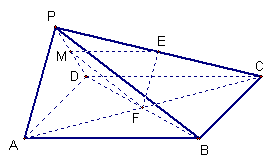 又
又![]() 面
面![]() 面
面![]() 面
面![]() ……………………………………………………………..10分
……………………………………………………………..10分
(Ⅲ)解:设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]() ,则
,则![]()
由(Ⅱ)知![]() 面
面![]() ,
, ![]()
![]() 面
面![]()
![]()
![]() 是二面角
是二面角![]() 的平面角……………………………………….12分
的平面角……………………………………….12分
![]() 中,
中,![]()
![]()
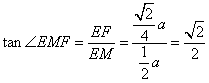 故所求二面角的正切值为
故所求二面角的正切值为![]() ……………………………….14分
……………………………….14分
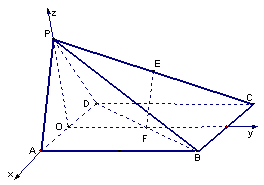 另解:如图,取
另解:如图,取![]() 的中点
的中点![]() , 连结
, 连结![]() ,
,![]() .
.
∵![]() , ∴
, ∴![]() .
.
∵侧面![]()
![]() 底面
底面![]() ,
,![]() ,
,
∴![]() ,
,
而![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,又
,又![]() 是正方形,故
是正方形,故![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
以![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴建立空间直线坐标系,则有
轴建立空间直线坐标系,则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵![]() 为
为![]() 的中点, ∴
的中点, ∴![]() .
.
(Ⅰ)易知平面![]() 的法向量为
的法向量为![]() 而
而![]() ,
,
且![]() , ∴
, ∴![]() //平面
//平面![]() .
.
(Ⅱ)∵![]() ,
,![]() ∴
∴![]() ,
,
∴![]() ,从而
,从而![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,而
,而![]() , ∴平面
, ∴平面![]() 平面
平面![]()
(Ⅲ)由(Ⅱ)知平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() .∵
.∵![]() ,
,
∴由![]() 可得
可得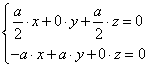 ,令
,令![]() ,则
,则![]() ,
,
故![]() ∴
∴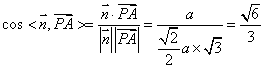 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() ,二面角
,二面角![]() 的正切值为
的正切值为![]() .
.
19.(本题满分14分)
本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.
(Ⅰ)证法一:由题设![]() 及
及![]() ,
,![]() ,不妨设点
,不妨设点![]() ,其中
,其中![]() .由于点
.由于点![]() 在椭圆上,有
在椭圆上,有![]() ,即
,即![]() .
.
解得![]() ,从而得到
,从而得到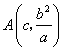 .
.
直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
由题设,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即![]() ,
,
将![]() 代入上式并化简得
代入上式并化简得![]() ,即
,即![]() .
.
证法二:同证法一,得到点![]() 的坐标为
的坐标为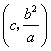 .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,易知
,易知![]()
![]()
![]() ,故
,故![]() .
.
 由椭圆定义得
由椭圆定义得![]() ,又
,又![]() ,
,
所以![]() ,
,
解得![]() ,而
,而![]() ,得
,得![]() ,即
,即![]() .
.
(Ⅱ)解法一:设点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,由
时,由![]() 知,直线
知,直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,或
,或![]() ,其中
,其中![]() ,
,![]() .
.
点![]() 的坐标满足方程组
的坐标满足方程组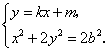
将①式代入②式,得![]() ,
,
整理得![]() ,
,
于是![]() ,
,![]() .
.
由①式得![]()
![]() .
.
由![]() 知
知![]() .将③式和④式代入得
.将③式和④式代入得![]() ,
,
![]() .
.
将![]() 代入上式,整理得
代入上式,整理得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,![]() 的坐标满足方程组
的坐标满足方程组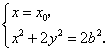
所以![]() ,
,![]() .
.
由![]() 知
知![]() ,即
,即![]() ,
,
解得![]() .
.
这时,点![]() 的坐标仍满足
的坐标仍满足![]() .
.
综上,点![]() 的轨迹方程为
的轨迹方程为 ![]() .
.
解法二:设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由
,由![]() ,垂足为
,垂足为![]() ,可知直线
,可知直线![]() 的方程为
的方程为![]() .
.
记![]() (显然
(显然![]() ),点
),点![]() 的坐标满足方程组
的坐标满足方程组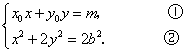
由①式得![]() . ③
. ③
由②式得![]() . ④
. ④
将③式代入④式得![]() .
.
整理得![]() ,
,
于是![]() . ⑤
. ⑤
由①式得![]() . ⑥
. ⑥
由②式得![]() . ⑦
. ⑦
将⑥式代入⑦式得![]() ,
,
整理得![]() ,
,
于是![]() . ⑧
. ⑧
由![]() 知
知![]() .将⑤式和⑧式代入得
.将⑤式和⑧式代入得![]() ,
,
![]() .
.
将![]() 代入上式,得
代入上式,得![]() .所以,点
.所以,点![]() 的轨迹方程为
的轨迹方程为![]() .
.
20.(本小题满分14分)
(本小题主要考查函数及其运算、不等式及其性质等基础知识,考查化归与转化、数形结合的数学思想方法,以及抽象概括能力、逻辑推理能力、运算求解能力和创新意识)
解:(Ⅰ)∵![]()
![]()
![]() ,
……2分
,
……2分
∵![]() ,∴
,∴![]() .∴实数
.∴实数![]() 的取值范围为
的取值范围为![]() .
……4分
.
……4分
(Ⅱ)∵![]() ,
,
显然![]() ,对称轴
,对称轴![]() .
……6分
.
……6分
(1)当![]() ,即
,即![]() 时,
时,![]() ,且
,且![]() .
.
令![]() ,解得
,解得![]() ,
,
此时![]() 取较大的根,即
取较大的根,即![]() ,
,
∵![]() ,∴
,∴![]() .
……10分
.
……10分
(2)当![]() ,即
,即![]() 时,
时,![]() ,且
,且![]() .
.
令![]() ,解得
,解得![]() ,
,
此时![]() 取较小的根,即
取较小的根,即![]() ,
,
∵![]() ,∴
,∴![]() .
……13分
.
……13分
当且仅当![]() 时,取等号.
时,取等号.
∵![]() ,∴当
,∴当![]() 时,
时,![]() 取得最小值-3.
……14分
取得最小值-3.
……14分
21.本小题以数列的递推关系式为载体,主要考查等比数列的前![]() 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解法一:![]() ,
,
![]() ,
,
![]() .
.
由此可猜想出数列![]() 的通项公式为
的通项公式为![]() .
.
以下用数学归纳法证明.
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设当![]() 时等式成立,即
时等式成立,即![]() ,
,
那么![]()
![]()
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]() 对任何
对任何![]() 都成立.
都成立.
解法二:由![]() ,
,![]() ,
,
可得![]() ,
,
所以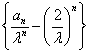 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故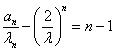 ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)解:设![]() , ①
, ①
![]() ②
②
当![]() 时,①式减去②式,
时,①式减去②式,
得![]() ,
,
![]() .
.
这时数列![]() 的前
的前![]() 项和
项和![]() .
.
当![]() 时,
时,![]() .这时数列
.这时数列![]() 的前
的前![]() 项和
项和![]() .
.
(Ⅲ)证明:通过分析,推测数列![]() 的第一项
的第一项![]() 最大,下面证明:
最大,下面证明:
![]() . ③
. ③
由![]() 知
知![]() ,要使③式成立,只要
,要使③式成立,只要![]() ,
,
因为![]()
![]()
![]() .
.
所以③式成立.因此,存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.