高三文科数学第一学期期末质量检查试题
数学试题（文科）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），完卷时间120分钟，满分，150分.
参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率Pn(k)=C
Pk(1－P)n－k
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共l2小题，每小题5分，共60分，在每小题给出的四个答案中，只有一项是符合题目要求的.
1．已知全集U=Z，A={－1，0，1，2}，B=
（ ）
A．{－1，2} B．{－1，0} C．{0，1} D．{1，2}
2．已知等差数列{an}中，a6+a10=20，a4=2，则a12的值是 （ ）
A．26 B．20 C．18 D．28
3．函数
(x≤2)的反函数的定义域是 （ ）
A．(－∞，9
B．[9，+∞] C．(0，9
D．(0，+∞)
4．圆
关于原点（0，0）对称的圆的方程为 （ ）
A．
B．
C．
D．
5．已知sin(α－
)=
，则cos (α +)的值等于 （ ）
A．
B．一 C．一
D．
6．若平面四边形ABCD满足
，则该四边形一定是（ ）
A．直角梯形 B．矩形 C．菱形 D．正方形
7．我们可以用以下方法来求方程
的近似根：设
，由
，可知方程必有一根在区间（0，1）内，再由
，可知方程必有一根在区间（0.5，1）内，依此类推，可将根所在的区间不断缩小，缩小到理想小的范围之内后，即可求方程的近似根. 据此可知方程
的根所在的区间是 （ ）
A．（－1，0） B．（0，1） C．（1，2） D．（2，3）
8．把四个不同的小球全部随意放人三个不同的盒子中，使每个盒子都不空的放法种数为
（ ）
A．
B．
C．
D．
9．若定义在R上的奇函数
满足
，则
等于 （ ）
A．0 B． 1 C．－ D．
|
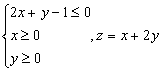的最大值为L，最小值为l，则L一l的值为（ ）
A．
B．1
C．
D．2
11．已知双曲线
(mn≠0)的离心率为2，且有一个焦点与抛物线y2=4x的焦点重合，则mn的值为 （ ）
A． B． C． D．
12．若
，则下列不等式一定成立的是 （ ）
A．
B．
C．
D．
|
二、填空题：本大题共4小题，每题4分，共l 6分.
13．某地区有农民家庭1600户，工人家庭400户，其它类家庭100户，现用分层抽样的方法从所有家庭中抽取一个容量为n的样本，已知从农民家庭中抽取了80户，则n=
14．二项式
展开式中第三项的系数为a，第四项的系数为b，则a－b=
15．不等式
的解集是
，则实数a=
16．关于函数
有下列命题：①
的周期为
；②
是的一条对称轴；③
的一个对称中心；④将的图象向右平移
个单位，可得到
的图象.
其中正确的命题序号是 （把你认为正确的命题的序号都写上）.
三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
17．（本题满分l2分）
在ΔABC中，角A、B、C的对边分别为a、b、c，4cos2
一cos2C =，a+b=5，c=
.
（1）求角C的大小；
（2）求ΔABC的面积.
18．（本题满分12分）
已知在等比数列{an}中，al+a3=l0，a2+a4=20，设cn=11一log2 a2n.
（I）求数列{cn}的通项；
（Ⅱ）求数列{cn}前n项和Sn的最大值.
19．（本题满分l 2分）
在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，记z=x一2 + y一x. 求z的所有可能的取值，并求出z取相应值时的概率.
20．（本题满分1 2分）
一群猴子第一天摘下若干个桃子，当即吃了
，还不过瘾，又吃了两个. 第二天早上又将剩下的桃子吃掉，又吃了两个. 以后每天早上都吃掉前一天剩下的后还要吃两个. 记
为第n天还没吃时桃子的个数.
（Ⅰ）证明：{+3}是等比数列；
（Ⅱ）若到第七天早上想吃时，只剩下一个桃子了，求第一天共摘了多少个桃子？
21．（本小题满分12分）
已知点A、B的坐标分别是（－1，0），（1，0）. 直线AM，BM相交于点M，且它们的斜率之积为－2.
（Ⅰ）求动点M的轨迹方程；
（Ⅱ）若过点
的直线l交动点M的轨迹于C、D两点，且N为线段CD的中点，求直线l的方程.
22．（本小题满分1 4分）
已知函数
（Ⅰ）要使
上单调递增，试求a的取值范围；
（Ⅱ）当a<0时，若函数满足
的解析式；
（Ⅲ）当
图象上任意一点处的切线的倾斜角为
的取值范围.
参考答案
一、选择题
1.A 2.C 3.C 4.A 5.C 6.C 7.D 8.B 9.D 10.D 11.A 12.A
|
13．105
14．－100 15． 16．①③
三、解答题
17．解：（1）由
整理，得
………………4分
解得
………………6分
（2）由余弦定理得c2=a2+b2－2abcocC，C=
∴
…………8分
又
………………10分
∴
…………12分
18．解：（1）设等比数列{an}的公比为q，则
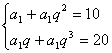………………2分
解得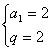
∴
………………4分
…………6分
（Ⅱ）{cn}是以9为首项，以－2为公差的等差数列
∴
………………9分 
所以当n=5时，数列{cn}前n项和Sn的最大值为25 …………12分
19．（本小题满分12分）
解：z的所有可能取值为0，1，2，3 ………………2分
当z=0时，只有x=2，y=2这一种情况，………………32分
z=1时，有x=1，y=1或x=2，y=1或x=2，y=3或x=3，y=3四种情况，…………4分
z=2时，有x=1，y=2或x=3，y=2两种情况 ………………5分
z=3时，有x=1，y=3或x=3，y=1两种情况 ………………6分
∴有放回抽两张卡片的所有情况有3×3=9种 …………8分
∴
…………12分
20．（本小题满分12分）
（Ⅰ）证明：由题意可得：
………………2分
所以
………………4分
又
是等比数列
…………6分
（Ⅱ）解：由（Ⅰ）可求得设
…………8分
又
…………10分
解得x=2913，即第一天猴子共摘了2913个桃子 …………12分
21．（本小题满分12分）
解：（Ⅰ）设M（x，y） …………1分
因为
…………3分
化简得：
………………4分
（Ⅱ）解：当直线
轴时，直线l的方程为
，其中点不是N，不合题意 ………………6分
当l不垂直于x轴时，设直线l的方程为
化简得 
据题意有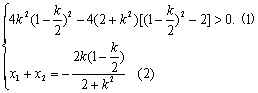 
…………9分
又由已知为线段CD的中点，得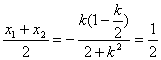
，解得k=－1
将k=－1代入（1）式中可知满足条件
此时直线l的方程为
，即所求直线l的方程为
……12分
22．（本小题满分14分）
（Ⅰ）
在（0，2）上单调递增，则
在（0，2）上恒成立 ………………2分
∵
是开口向下的抛物线 ∴
…………4分
（Ⅱ）令
∵
∴
∴
………………8分
（Ⅲ）∵
据题意 
上恒成立
………………10分
由 
由
又
…………13分
综上，a的取值范围是