高三文科数学第四次统一测试

高三文科数学第四次统一测试

数学试题（文科）

本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分，答题时间120分钟。

第Ⅰ卷（选择题，共50分）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确的选项填在答题卡的表格里（每小题5分，共50分）．

1．下列命题是真命题的是（　　）

(A) 集合是空集　　

(B) 设集合，则的充要条件是 　　　　　　　　　　

(C) 若，则　　　(D) 向量与向量共线

2．已知a＞b＞0，全集为R，集合，，，则有（　　）

(A)  　　　　　　　　　　　　　 (B)

(C)　　　　　　　　　　　　　　　　　 (D)

3．等比数列中，且，则（　  ）

(A) 9　　　　　 (B) 6　　　　　　 (C) 3　　　　　  (D) 2

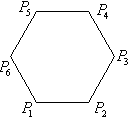4．如右图,已知正六边形P₁P₂P₃P₄P₅P₆,下列

向量的数量积中最大的是（　　）

(A)　　　　　　 (B)

(C)　　　　　　 (D)

5．下列函数中，在其定义域内既是奇函数，又是减函数的是( 　 )

(A) 　　　　　(B)   

(C) 　　　　　　　　 (D)

6．函数f (x ) = x³－3x + 1在闭区间[－3，0]上的最大值、最小值分别是（　　）

(A) 1，－1　　　 (B) 1，－17 　　 (C) 3，－17　　　(D) 9，－19

7．实数x，y满足不等式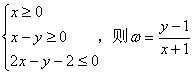的取值范围是（　　）

　　　 (A) 　　　　　　　　　　　　　　　　　　　　　　 (B) [－1，1]

　　　 (C)　　　　　　　　　　　　　　　(D)

8．若四边形中，满足则该四边形是（ 　 ）

(A) 菱形　　　 (B) 直角三角形　　(C) 矩形　　　 (D) 正方形

9．设等差数列的前n项和为，若则使成立的最大自然数n为（　 　）

(A) 4005　　　 (B) 4006　　　　　 (C) 4007　　　  (D) 4008

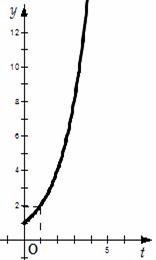10．如图所示是某池塘中浮萍的面积与时间(月)的关系,

有以下叙述:

① 这个指数函数的底数为2;

② 第5个月时, 浮萍面积就会超过30;

③ 浮萍每月增加的面积都相等;

④ 若浮萍蔓延到2, 3, 6所经过的时间

分别是, 则.

其中正确的是 (　　 )　

(A) ①②　　　　　 (B) ①②④

(C) ②④③　　　　 (D) ①④

第Ⅱ卷（非选择题，共100分）

二、填空题：请把答案填在答题卡中的横线上（每小题5分，共20分）．

11．要得到的图象, 且使平移的距离最短, 则需将的图象

向　　　　  方向平移　　　　　 个单位即可得到;

12．在△ABC中，分别是所对的边，若

则 　　　　　;

13．在R上为减函数，则的取值范围是　　　　　　　;

14．在直角坐标平面内，已知点列P₁（1、2），P₂（2，2²），P₃（3，2³），…，P_n（n,2ⁿ），…如果n为正整数，则向量的坐标为　　 　　　　.（用n表示）（资料来源：南方学科网　 www.nfxk.com）

三、解答题：解答应写出文字说明、证明过程或演算步骤(共80分)．

15．(本题满分12分)

已知函数.

（1）求函数的最小正周期、最大值和最小值；

（2）若，求的值。

16．(本题满分12分)

已知向量, , .

（1）求的值;　 （资料来源：南方学科网　 www.nfxk.com）

（2）若, , 且, 求.

17．（本小题满分14分）

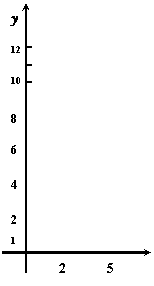
某民营企业生产两种产品，据市场调查与预测，A产品的利润（y）与投资额(x)成正比，其关系如图1所示，B产品的利润（y）与投资额(x)的算术平方根成正比，其关系如图2所示（注：利润与投资单位为万元）

（1）分别将A、B两种产品的利润表示为投资的函数关系式；

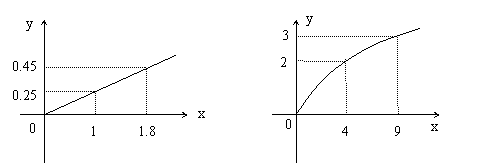（2）该企业已筹集到8万元资金，并全部投入A、B两种产品的生产，问：怎样分配这8万元投资，才能使企业获得最大利润？其最大利润为多少万元？

18．（本小题满分14分）

已知等差数列的前六项和为60，且

　（1）求数列的通项公式

（2）若数列满足且

19．(本题满分14分)

已知函数f（x）的图像与函数的图像关于点A（0，1）对称．

　（1）求f（x）的解析式；

　（2）若，且在区间（0，上为减函数，求实数a的取值范围．

20. (本题满分14分)

已知二次函数满足条件:

①;　②的最小值为.

（1）求函数的解析式;

（2）设数列的前项积为, 且, 求数列的通项公式;

（3）在（2）的条件下, 若是与的等差中项, 试问数列中第几项的值最小? 求出这个最小值.