高三理科数学12月月考试卷
高三数学(理科)
命题人:张宏汉 审题人:杨红云
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的)
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则A![]() (CUB)= ( )
(CUB)= ( )
A. {2} B. {2,3} C. {1,3} D. {3}
2.已知![]() ,且
,且![]() ,则
,则![]()
![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
3.等差数列![]() 的公差为2,若a1、a3、a4成等比数列,则a2= (
)
的公差为2,若a1、a3、a4成等比数列,则a2= (
)
A.-6 B.-8 C.8 D.6
4.设b、c表示两条直线,![]() 、β表示两个平面,下列命题中真命题是 ( )
、β表示两个平面,下列命题中真命题是 ( )
A.若b![]()
![]() ,c∥
,c∥![]() ,则b∥c B.若b
,则b∥c B.若b![]()
![]() ,b∥c,则c∥
,b∥c,则c∥![]()
C.若c∥![]() ,c⊥β,则
,c⊥β,则![]() ⊥β D.若c∥
⊥β D.若c∥![]() ,
,![]() ⊥β,则c⊥β
⊥β,则c⊥β
5.已知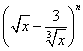 展开式中,各项系数的和为64,则
展开式中,各项系数的和为64,则![]() 等于 ( )
等于 ( )
A. 7 B. 6 C. 5 D. 4
6.已知抛物线![]() 的准线与双曲线
的准线与双曲线![]() 的一条准线重合,则这条抛物线
的一条准线重合,则这条抛物线![]() 与双曲线
与双曲线![]() 的交点P到抛物线焦点的距离为 ( )
的交点P到抛物线焦点的距离为 ( )
A.![]() B.21
C.6
D.4
B.21
C.6
D.4
7. 设三棱锥的3个侧面两两互相垂直,且侧棱长均为![]() ,则其外接球的表面积为 ( )
,则其外接球的表面积为 ( )
A.![]() B.
B.
![]() C.
C. ![]() D.
D.![]()
8.某小组有4名男生,5名女生,从中选派5人参加竞赛,要求有女生且女生人数少于男生人数的选派方法种数有 ( )
A. 40 B. 45 C. 105 D. 110
9. 已知直线![]() 按向量
按向量![]() 平移后得到的直线
平移后得到的直线![]() 与圆
与圆![]() 相切,那么
相切,那么![]() 的值为 ( )
的值为 ( )
A.9或-1 B.5或-5 C.-7或7 D.-1或9
10.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已
知加密规则为:明文![]() 对应密文
对应密文![]() ,例如,
,例如,![]() 对应密文
对应密文
![]() .当接收方收到密文
.当接收方收到密文![]() 时,则解密得到的明文为
( )
时,则解密得到的明文为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知![]() 是其定义域上的单调递增函数,它的反函数是
是其定义域上的单调递增函数,它的反函数是![]() 的图象过A(-4,0),B(2,3)两点,若
的图象过A(-4,0),B(2,3)两点,若![]() ,则x的取值范围是 ( )
,则x的取值范围是 ( )
A.[0,3] B.[-4,2] C.[1,3] D.[-1,2]
12.口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列![]() :
:![]() ,如果
,如果![]() 为数列
为数列![]() 的前
的前![]() 项和,那么
项和,那么![]() 的概率为 ( )
的概率为 ( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 高三数学(理科)
高三数学(理科)
| 题 号 | 一 | 二 | 三 | 总分 |
| 得 分 |
|
|
|
|
 二、填空题:本大题共4小题,每小题5分,共20分。把答案填在题中相应的横线上。
二、填空题:本大题共4小题,每小题5分,共20分。把答案填在题中相应的横线上。
13.已知函数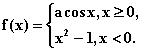 在点x=0处连续,则a=
.
在点x=0处连续,则a=
.
14.设![]() ,
,![]() 为正数 ,则
为正数 ,则![]() 的最小值是 .
的最小值是 .
15.若不等式![]() 无解,则
无解,则![]() 的取值范围是
.
的取值范围是
.
16.给出下列命题
①若命题P和命题Q中只有一个是真命题,则![]() P或Q是假命题;
P或Q是假命题;
②![]() 或
或![]() 是
是![]() 成立的必要不充分条件;
成立的必要不充分条件;
③若函数y=f(x)满足![]() 是周期函数;
是周期函数;
④若![]() ,则r的取值范围是
,则r的取值范围是![]() .
.
其中所有正确命题的序号是 .
三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.
 17.(本题满分10分) 某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9.
17.(本题满分10分) 某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9.
(Ⅰ)求在一年内李明参加驾照考试次数![]() 的分布列和
的分布列和![]() 的期望;
的期望;
(Ⅱ)求李明在一年内领到驾照的概率.
 18.(本题满分10分)设函数
18.(本题满分10分)设函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,a、 b、 c分别是角A、B的对边,
![]() ,求b,c的长.
,求b,c的长.

19.(本题满分12分) 如图,已知三棱锥![]() 的侧棱
的侧棱![]() 两两垂直,且
两两垂直,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
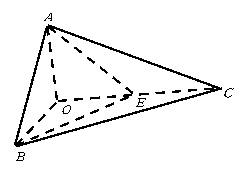 (1)求
(1)求![]() 点到面
点到面![]() 的距离;
的距离;
(2)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(3)求二面角![]() 的大小.
的大小.
 20. (本题满分12分)已知函数
20. (本题满分12分)已知函数![]() ,
,
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)求![]() 的单调区间;
的单调区间;
21.(本题满分12分)已知方向向量为![]() 的直线
的直线![]() 过椭圆C:
过椭圆C:![]() 的焦点以及点(0,
的焦点以及点(0,![]() ),椭圆C的中心关于直线
),椭圆C的中心关于直线![]() 的对称点在椭圆C的右准线上.
的对称点在椭圆C的右准线上.
 (Ⅰ)求椭圆C的方程.
(Ⅰ)求椭圆C的方程.
(Ⅱ)是否存在过点E(-2,0)的直线![]() 交椭圆C于点M、N,使△MON的面积为
交椭圆C于点M、N,使△MON的面积为![]() ,(O为坐标原点)?若存在,求出直线
,(O为坐标原点)?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 22.(本题满分14分)已知定义在R上的单调函数
22.(本题满分14分)已知定义在R上的单调函数![]() 对任意的实数
对任意的实数![]() ,
,![]() ,都有
,都有![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)数列![]() 满足
满足![]() 且
且![]()
①求通项公式![]() 的表达式;
的表达式;
②令![]() ,
,![]() ,
,![]() 试比较
试比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
高三理科数学参考答案及评分标准(12月)
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | C | B | D | B | B | A | C | D | B |
二、填空题:
13.-1 14.9
15.![]() 16.②③④
16.②③④
三、解答题:
17.(本题满分10分)解:(Ⅰ) ![]() 的取值分别为1,2,3,4.
的取值分别为1,2,3,4.
![]() ,表明李明第一次参加驾照考试就通过了,故P(
,表明李明第一次参加驾照考试就通过了,故P(![]() )=0.6.
)=0.6.
![]() ,表明李明在第一次考试未通过,第二次通过了,故
,表明李明在第一次考试未通过,第二次通过了,故
![]()
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
![]()
ξ=4,表明李明第一、二、三次考试都未通过,故
![]() ……………(4分)
……………(4分)
∴李明实际参加考试次数ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | 0.6 | 0.28 | 0.096 | 0.024 |
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544. ……………(6分)
(Ⅱ)李明在一年内领到驾照的概率为
1-(1-0.6)(1-0.7)(1-0.8)(1-0.9)=0.9976. ……………(10分)
18.(本题满分10分)
解(Ⅰ)![]()
![]()
![]() ……………4分
……………4分
∴![]() ……………5分
……………5分
(Ⅱ)f (A) = 2, 即![]()
![]()
∴b2 + c2-bc = 3 ①
又b2 + c2 + 2bc = 9 ②
②-① bc = 2 ③ ……………8分
b + c = 3 ④
b > c ⑤
由③,④解出![]() ……………10分
……………10分
19:. (本题满分12分) (1)取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]()
![]() 、
、![]()
![]()
则![]() 面
面![]() ,
,![]() 的长就是所要求的距离.
的长就是所要求的距离.![]()
![]() 、
、![]() ,
,
![]()
![]() ,在直角三角形
,在直角三角形![]() 中,有
中,有![]()
(另解:由![]() ……………4分
……………4分
(2)取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]() ,则
,则![]() ∥
∥![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角.求得:
所成的角.求得: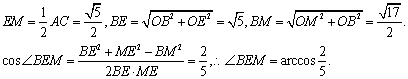
……………8分
(3)连结![]() 并延长交
并延长交![]() 于
于![]() ,连结
,连结![]() 、
、![]() .
.
![]()
则![]() 就是所求二面角的平面角.作
就是所求二面角的平面角.作![]() 于
于![]() ,则
,则![]()
在直角三角形![]() 中,
中,![]()
在直角三角形![]() 中,
中,![]()
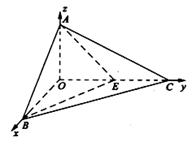
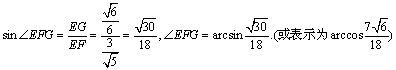 ……………12分
……………12分
方法二:(1)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则有![]() 、
、![]() 、
、![]() 、
、![]()
设平面![]() 的法向量为
的法向量为![]()
则由![]()
由![]()
![]() ,则点
,则点![]() 到面
到面![]() 的距离为
的距离为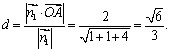 ……4分
……4分
![]()
![]() <
<![]() >
>![]() 所以异面直线
所以异面直线![]() 与
与![]() 所成的角
所成的角![]() . ………8分
. ………8分
(3)设平面![]() 的法向量为
的法向量为![]() 则由
则由![]() 知:
知:![]()
由![]() 知:
知:![]() 取
取![]()
由(1)知平面![]() 的法向量为
的法向量为![]()
则![]() <
<![]() >
>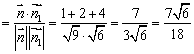 .
.
结合图形可知,二面角![]() 的大小为:
的大小为:![]() .
……………12分
.
……………12分
20.(本题满分12分)
解:(1)∵![]() ,
,
∴![]() =
=![]() =
=![]() ……………3分
……………3分
令![]() ,得
,得![]() =2,
=2,![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴在区间![]() 上,
上,![]() =2时,
=2时,![]() 最大=
最大=![]() ;
;
![]() ;而
;而![]() ,
,![]() =
=![]()
![]()
![]()
∴![]()
![]() ……………6分
……………6分
(2)∵![]() ,∴
,∴![]() =
=![]() ……………8分
……………8分
①当![]() 时,由
时,由![]() 得:
得:![]() 0,由
0,由![]() 得:
得:![]() 0,又
0,又![]()
∴![]() 在
在![]() 为增函数
为增函数
②当![]() 时,
时,![]() =
=![]() =
=![]()
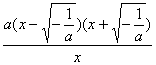
由![]() 得:
得: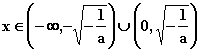
由![]() 得:
得: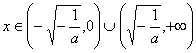 又
又![]()
∴![]() 的单调增区间是
的单调增区间是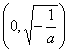 ;减区间是
;减区间是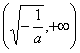 ……………12分
……………12分
21.(本题满分12分)
解:⑴直线![]() ①,过原点垂直于
①,过原点垂直于![]() 的直线方程为
的直线方程为![]() ②
②
解①②得![]() .
……………2分
.
……………2分
∵椭圆中心O(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴![]() , ………(3分)
, ………(3分)
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0),
……………4分
过椭圆焦点,∴该焦点坐标为(2,0),
……………4分
∴![]() ,故椭圆C的方程为
,故椭圆C的方程为![]() ③ ……………6分
③ ……………6分
⑵当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 代入③并整理得
代入③并整理得
![]() ,
,
设![]() ,则
,则![]()
![]() ……………8分
……………8分
∴![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离 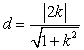 ,
……………10分
,
……………10分
∵![]() , ∴
, ∴![]() ,即
,即![]()
解得 ![]() ,此时
,此时![]()
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,也有
,也有![]()
故存在直线![]() 满足题意,其方程为
满足题意,其方程为![]() .
……………12分
.
……………12分
22、(本题满分14分)
(1)令y=0得f(x)[1-f(0)]=0,则f(0)=1 ……………3分
(2)①由递推关系知![]()
从而![]() ……………6分
……………6分
②![]() 的大小,只需比较
的大小,只需比较![]() 的大小,由=1,2,3代入可知4n>2n+1,猜想4n>2n+1. ……………10分
的大小,由=1,2,3代入可知4n>2n+1,猜想4n>2n+1. ……………10分
下面用数学归纳法证明
(i)当n=1时,41>2×1+1成立
(ii)假设当n=k时命题成立,即4k>2k+1
当n=k+1时,4k+1=4×4k>4(2k+1)=8k+4=2(k+1)+1+6k+1>2(k+1)+1,
说明当n=k+1时命题也成立.
由(i)(ii)可知,4n>2n+1 对于n∈N*都成立.
故Sn>![]() .………………………………………………………………14分
.………………………………………………………………14分
注:证明4n>2n+1,除用数学归纳法证明以外,还可用其它方法证明,
如:4n=(1+3)n=1+![]()