高三数学科第一学期期末联考试卷
考试时间120分钟,满分150分
命题人:郑启文 审核人:张神驹
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知条件![]() ( )
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知两定点![]() 、
、![]() 且
且![]() 是
是![]() 与
与![]() 的等差中项,则动点P的轨迹方程是( )
的等差中项,则动点P的轨迹方程是( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
3.已知ABCD是边长为1的正方形,设![]() ( )
( )
A.1
B.![]() C.
C.![]() D.2
D.2
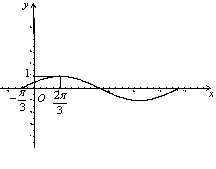 4.若函数
4.若函数![]() (
(![]() )
)
的部分图象如图所示,则有( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.正四棱柱的底面边长是1,侧棱长是2,它的八个顶点都在同一个球面上,则这个球的表面积为( )
A.6 B.![]() C.
C.![]() D.
D.![]()
6.过抛物线![]() 的焦点作一条直线与抛物线相交于A、B两点,且AB弦长为7,则这样的直线(
)
的焦点作一条直线与抛物线相交于A、B两点,且AB弦长为7,则这样的直线(
)
A. 不存在 B. 有无穷多条 C. 有且仅有一条 D. 有且仅有两条
7.将函数![]() 的图象向左平移m个单位所得的图象关于
的图象向左平移m个单位所得的图象关于![]() 轴对称,则
轴对称,则![]() 最小正值是( )
最小正值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知![]() 、
、![]() 是两个不同平面,
是两个不同平面,![]() 、
、![]() 是两不同直线,下列命题中的假命题是( )
是两不同直线,下列命题中的假命题是( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
9.若f (x)=![]() (a>0且a
(a>0且a![]() 1),满足
1),满足![]() ,则函数f (x)的图像沿
,则函数f (x)的图像沿![]() = (
= (![]() ,0)平移后的图像大致是( )
,0)平移后的图像大致是( )

10.从圆![]() 外一点
外一点![]() 向这个圆作两条切线,则两切线夹角的余弦值为 ( )
向这个圆作两条切线,则两切线夹角的余弦值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.等差数列![]() 中,
中,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为( )
的值为( )
A.14 B.15 C.16 D.18
| |
 则
则A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
第II卷(非选择题,共90分)
二、填空题:本大题有4小题,每小题4分,共16分. 把答案填在题中横线上.
13.函数![]() 的定义域是
。
的定义域是
。
14.若数列![]() 满足
满足![]() 是首项为1,公比为2的等比数列,则
是首项为1,公比为2的等比数列,则![]() 等于
。
等于
。
15.设实数![]() 满足约束条件:
满足约束条件: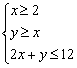 ,则
,则![]() 的最大值为 .
的最大值为 .
16.下列函数①![]() ;②
;②![]() ;
;
③![]() ;④
;④![]() 中,满足“存在与x无关的正常数M,使得
中,满足“存在与x无关的正常数M,使得![]() 对定义域内的一切实数x都成立”的有 (把满足条件的函数序号都填上).
对定义域内的一切实数x都成立”的有 (把满足条件的函数序号都填上).
三、解答题:本大题有6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分12分) 已知![]() ,且
,且![]()
(1)求![]() 的值;
的值;
(2)求![]() 的值。
的值。
18.(本小题满分12分)已知函数f(x)=ax2+(b-8)x-a-ab , 当x![]() (-∞,-3)
(-∞,-3)![]() (2,+∞)时, f(x)<0,当x
(2,+∞)时, f(x)<0,当x![]() (-3,2)时f(x)>0 .
(-3,2)时f(x)>0 .
(1)求f(x)在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
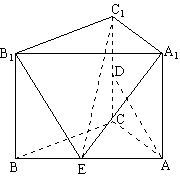 19.(本小题满分12分)
19.(本小题满分12分)
如图,在直三棱柱ABC—A1B1C1中, AA1=4,AB=5,BC=3,AC=4,D为CC1的中点。
(1)求异面直线AD与A1B1所成角的余弦值;
(2)试在线段AB上找一点E,使得:A1E⊥AD;
(3)求点D到平面B1C1E的距离。
20.(本小题满分12分)
某高速公路指挥部接到通知,24小时后将有一场超历史记录的大暴雨,为确保万无一失,指挥部决定在24小时内筑一道临时堤坝,以防山洪淹没正在紧张施工的隧道工程。经测算,除现有施工人员外,还须调用翻斗车搬运![]() 立方米的土方。已知每辆翻斗车每小时可搬运的土方量为
立方米的土方。已知每辆翻斗车每小时可搬运的土方量为![]() ,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
(1)从第一辆车投入施工算起,第25辆车须多久才能到达?
(2)24小时内能否完成防洪堤坝工程?请说明理由。
21.(本小题满分12分) ![]() 是以
是以![]() 为焦点的双曲线C:
为焦点的双曲线C:![]() (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知![]() =0,
=0,![]() .(1)试求双曲线的离心率
.(1)试求双曲线的离心率![]() ;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当
;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当![]() =-
=-![]() ,
,![]() =
=![]() ,求双曲线的方程.
,求双曲线的方程.
22.(本小题满分14分)已知数列{![]() }中,
}中,![]() (n≥2,
(n≥2,![]() ),
),
(1)若![]() ,数列
,数列![]() 满足
满足![]() (
(![]() ),求证数列{
),求证数列{![]() }是等差数列;
}是等差数列;
(2)在(1)的情况下,求数列{![]() }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)若![]() ,试证明:
,试证明:![]() .
.
答案
一、选择题:
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. |
| A | C | D | C | C | D | A | B | B | B | C | D |
二、填空题:
13. ![]() ; 14.
; 14.![]() ; 15. 68; 16. ② ③
; 15. 68; 16. ② ③
三、解答题:
17. (1)由![]() 得
得![]() ……………………………… 2分
……………………………… 2分
![]() …………6分
…………6分
(2)原式![]()
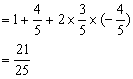 ……………………12分
……………………12分
18、解 (1)由题意得a<0且ax2+(b-8)x-a-ab=0的根为-3,2……………2分
-3+2=![]() ,(-3)×2=
,(-3)×2=![]()
![]() ,从而a=-3,b=5……………………4分
,从而a=-3,b=5……………………4分
f(x)=-3x2-3x+18,对称轴为x=![]() ,可得f(x)∈[12,18]
………………7分
,可得f(x)∈[12,18]
………………7分
(2)由-3x2+5x+c≤0得c≤3x2-5x恒成立,得c≤-![]() …………………… 12分
…………………… 12分
19.解:(1)在直三棱柱ABC—A1B1C1中,
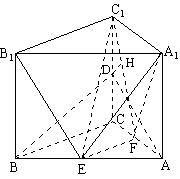 (1)∵
(1)∵![]() ,
,
∴![]() (或其补角)为异面直线AD与A1B1所成的角,
(或其补角)为异面直线AD与A1B1所成的角,
………………………2分,连结BD,
在![]() 中,∵AC=4,
中,∵AC=4,![]()
∴![]() ,
,
在![]() 中,∵BC=3,CD=2,∴
中,∵BC=3,CD=2,∴![]() ,
,
在△ABD中,∵AB=5,![]()
∴异面直线AD与A1B1所成角的余弦值为![]() ………………………………4分
………………………………4分
(2)证明:∵AB=5,BC=3,AC=4,∴![]() ,
,
∵底面ABC⊥侧面ACC1A1,∴BC⊥侧面ACC1A1,………………………………6分
取AB、AC的中点E、F,连结EF、A1F,则EF//BC,
∴EF⊥平面ACC1A1, ∴A1F为A1E在侧面AC1内的射影,
在正方形C1CAA1内,∵ D、F分别为CC1、AC的中点,
∴![]() ≌
≌![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() (三垂线定理)………………8分
(三垂线定理)………………8分
(3)连结![]() ,过D作DH⊥
,过D作DH⊥![]() ,垂足为H。
,垂足为H。
∵EF//BC,BC//B1C1,∴EF// B1C1,∴点F在平面B1C1E内。
∵EF⊥平面ACC1A1,![]() 平面ACC1A1,EF⊥DH,………………10分
平面ACC1A1,EF⊥DH,………………10分
∵![]() ,
,![]() ,∴DH⊥平面B1C1E。
,∴DH⊥平面B1C1E。
在![]() 中,∵
中,∵![]() ,∴
,∴![]() 。……………12分
。……………12分
(本题用空间向量法来解,每小题对应给分)
20.解:(1)设从第一辆车投入施工算起,各车到达时间依此为![]() 、
、![]() 、…、
、…、![]() ,依题意,它们组成一个首项为0,公差为
,依题意,它们组成一个首项为0,公差为![]() (小时)的等差数列,…………3分
(小时)的等差数列,…………3分
则![]() =
=![]() +24d,∴
+24d,∴![]() =24×
=24×![]() =8,
=8,
答:第25辆车须8小时后才能到达。………………6分
(2)设从第一辆车投入施工算起,各车的工作时间依次为![]() 、
、![]() 、…、
、…、![]() ,依题意,它们组成一个公差为-
,依题意,它们组成一个公差为-![]() (小时)的等差数列,且
(小时)的等差数列,且![]() ………………8分
………………8分
∵每辆车每小时的工作效率为![]() ,∴
,∴![]()
即![]() ,……………………10分
,……………………10分
又∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
由于![]() ,可见
,可见![]() 的工作时间可以满足要求,即工程可以在24小时内完成。
的工作时间可以满足要求,即工程可以在24小时内完成。
答:24小时内能完成防洪堤坝。………………………………………………12分
21.解(1)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴![]() .…………………4分
.…………………4分
(2)由(1)知,双曲线的方程可设为![]() ,渐近线方程为
,渐近线方程为![]() .……5分
.……5分
设P1(x1,2x1),P2(x2,-2x2),P(x,y).………………………………………6分
∵![]() ,∴
,∴![]() . ∵
. ∵![]() ,∴
,∴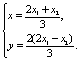 …………10分
…………10分
∵点P在双曲线上,∴![]() .
.
化简得,![]() .∴
.∴![]() .∴
.∴ ![]() .∴双曲线的方程为
.∴双曲线的方程为![]() …………12分
…………12分
22.(1)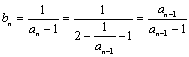 ,而
,而 ![]() ,
,
∴ ![]() .
.![]()
∴ {![]() }是首项为
}是首项为![]() ,公差为1的等差数列.…………… 4分
,公差为1的等差数列.…………… 4分
(2)由(1)有![]() ,而
,而![]() , ∴
, ∴ ![]() .对于函数
.对于函数![]() ,在x>3.5时,y>0,
,在x>3.5时,y>0,![]() ,在(3.5,
,在(3.5,![]() )上为减函数.
)上为减函数.
故当n=4时,![]() 取最大值3. ……………………………… 6分
取最大值3. ……………………………… 6分
而函数![]() 在x<3.5时,y<0,
在x<3.5时,y<0,![]() ,在(
,在(![]() ,3.5)上也为减函数.故当n=3时,取最小值,
,3.5)上也为减函数.故当n=3时,取最小值,![]() =-1. ……………………………………… 8分
=-1. ……………………………………… 8分
(3)
用数学归纳法证明![]() ,再证明
,再证明![]()
① 当![]() 时,
时,![]() 成立; ……………………………………… 9分
成立; ……………………………………… 9分
②假设当![]() 时命题成立,即
时命题成立,即![]() ,
,
当![]() 时,
时,![]()
![]()
![]()
![]()
故当![]() 时也成立, ……………………………………… 11分
时也成立, ……………………………………… 11分
综合①②有,命题对任意![]() 时成立,即
时成立,即![]() . …………12分
. …………12分
(也可设![]() (1≤
(1≤![]() ≤2),则
≤2),则![]() ,
,
故![]()
![]()
![]() ).
).
下证:![]()
![]()
![]()
![]() .………………………14分
.………………………14分
(本小题若不用数学归纳法证明,需对应给分。)