高三数学第一学期期中考试试题
高三数学试题
第Ⅰ卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共60分).
1.设A,B是两个非空集合,定义A×B=![]() ,已知
,已知
![]() 则A×B= ( )
则A×B= ( )
A.![]() B.
B.![]() C.[0,1] D.[0,2]
C.[0,1] D.[0,2]
2.在![]() 的大小为 ( )
的大小为 ( )
A.30° B. 60° C.120° D. 150°
3.设![]() 在[a,b]上可导,且
在[a,b]上可导,且![]() ,则当
,则当![]() 时有 ( )
时有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
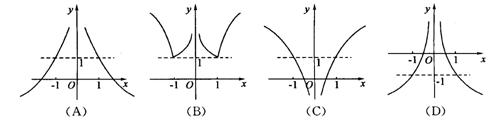
4.函数![]() 的图象大致为 ( )
的图象大致为 ( )
5.设函数![]() 是偶函数,则
是偶函数,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
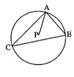 6.如图,点P为△ABC的外心,且
6.如图,点P为△ABC的外心,且![]() ,则
,则![]()
等于 ( )
A.2 B.4
C.6 D.8
7.先作函数![]() 的图像关于原点对称的图像,再将所得图像向右平移一个单位得图像C1,函数
的图像关于原点对称的图像,再将所得图像向右平移一个单位得图像C1,函数![]() 的图像C2与C1关于直线
的图像C2与C1关于直线![]() 对称,函数
对称,函数![]() 的解析式
的解析式
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设e<x<10,记a=ln(lnx),b=lg(lgx),c=ln(lgx),d=lg(lnx),则a,b,c,d的大小关系( )
A.a<b<c<d B.c<d<a<b C.c<b<d<a D.b<d<c<a
9.设![]() 的定义在R上以2为周期的偶函数,当
的定义在R上以2为周期的偶函数,当![]() 时,
时,![]() 则
则![]() 时,
时,![]() 的解析式为 ( )
的解析式为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.垂心 B.重心 C.内心 D.外心
11.设函数![]() ,则
,则![]() 有
( )
有
( )
A.分别位于 (1,2)(2,3)(3,4)内三个根
B.四个实根![]() (i=1,2,3,4)
(i=1,2,3,4)
C.分别位于 (0,1)(1,2)(2,3)(3,4)内四个
D.分别位于 (0,1)(1,2)(2,3)内三个根
12.设M是![]()
m、n、p分别是![]() 的最小值
的最小值
( )
A.8 B.9 C.16 D.18
|
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
13.设函数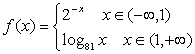 ,则满足
,则满足![]() 的
的![]() 值是_________
值是_________
14.(理科)由曲线![]() 所围成的图形面积是
所围成的图形面积是
(文科)函数![]() 的单调递增区间是
的单调递增区间是
15.已知在平面直角坐标系中,![]() 为原点,且
为原点,且![]() (其中
(其中![]() ),若N(1,0),则
),若N(1,0),则![]() 的最小值是
的最小值是
16.已知下列命题:①![]() ;②函数
;②函数![]() 的图像向左平移1个单位后得到的函数图像解析式为
的图像向左平移1个单位后得到的函数图像解析式为![]() ;③函数
;③函数![]() 的图像与函数
的图像与函数![]() 的图像关于
的图像关于![]() 轴对称; ④满足条件
轴对称; ④满足条件![]() 的三角形△ABC有两个.其中正确命题的序号是
的三角形△ABC有两个.其中正确命题的序号是
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
17.(本题12分)已知直线l的倾斜角为![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值.
的值.
18.(本题12分)已知函数![]()
(Ⅰ)求函数![]() 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)当![]() (其中e=2.718 28…是自然对数的底数);
(其中e=2.718 28…是自然对数的底数);
19.(本题12分)已知向量![]() 且
且![]()
(1)若![]() 求x的范围
求x的范围
(2)![]() 若对任意
若对任意![]() ,
,![]() 恒有
恒有![]() 求t的取值范围.
求t的取值范围.
20.(本题12分)已知函数![]() 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数![]() 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求a的值;
(II)求λ的取值范围
(III)若![]() 在
在![]() [-1,1]上恒成立,求t的取值范围.
[-1,1]上恒成立,求t的取值范围.
21.(本题12分)在△ABC中,a、b、c分别是角A、B、C的对边,![]()
| |
(Ⅱ)若a=7,求角C.
22.(本题14分) 已知函数![]() ,当
,当![]() 时,取得极小值
时,取得极小值![]() .
.
(1)求![]() 的值;
的值;
(2)对任意![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围;
的取值范围;
 (3)设直线
(3)设直线![]() ,曲线
,曲线![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 同时满足下列两个条件:①直线
同时满足下列两个条件:①直线![]() 与曲线
与曲线![]() 相切且至少有两个切点;②对任意
相切且至少有两个切点;②对任意![]() 都有
都有![]() ,则称直线
,则称直线![]() 与曲线
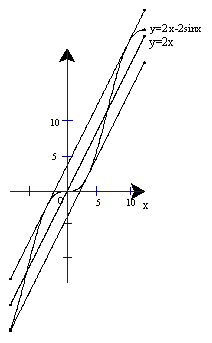
与曲线![]() 的“上夹线”.观察下图:
的“上夹线”.观察下图:
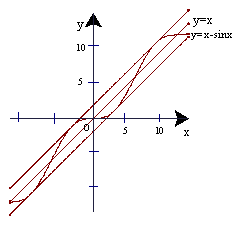 |
根据上图,试推测曲线![]()
的“上夹线”的方程,并作适当的说明.
高三数学第一学期期中考试试题
高三数学试题参考答案
1.A 2.D 3.C 4.A 5.B 6.A 7.A 8.C 9.B 10.C 11.A 12.D
|
17.解:![]()
![]() …………2分
…………2分
![]() …………4分
…………4分
(Ⅰ)![]() …………6分
…………6分
![]() …………8分
…………8分
(Ⅱ)![]() …………10分
…………10分
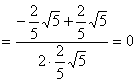 …………12分
…………12分
18.解:(Ⅰ)![]() …………2分
…………2分
![]() 上是单调递增函数.
上是单调递增函数.
![]()
同理,令![]()
∴f(x)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .……………………6分
.……………………6分
由此可知![]() …………………………………………8分
…………………………………………8分
(Ⅱ)由(I)可知当![]() 时,有
时,有![]()
![]() ………10分
………10分
即![]() .
.
![]() .……………………………………………………………………12分
.……………………………………………………………………12分
19.解::![]() …………2分
…………2分
(1)![]()
![]()
![]() …………………6分
…………………6分
(2)![]() …………………8分
…………………8分
![]()
![]() …………………10分
…………………10分
![]()
![]() …………………12分
…………………12分
20.解:(I)![]() 是奇函数,
是奇函数,
则![]() 恒成立.
恒成立.
![]()
![]() ……………………3分
……………………3分
(II)![]() 上是减函数,
上是减函数,
![]() 在[-1,1]上恒成立,
在[-1,1]上恒成立,
![]()
![]() …………………………………………………………………………6分
…………………………………………………………………………6分
(III)![]() 在[-1,1]上单调递减,
在[-1,1]上单调递减,
![]()
![]()
![]() ………………………………8分
………………………………8分
令![]()
则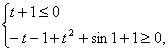 ……………………………………………………10分
……………………………………………………10分
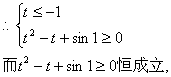
![]() .…………………………………………………………………………12分
.…………………………………………………………………………12分
21.(I)![]()
=![]() ………………………………3分
………………………………3分
又![]()
![]()
![]() …………………………6分
…………………………6分
(Ⅱ)由(Ⅰ)知ac=35,又a=7,∴c=5,
![]() ,………………………9分
,………………………9分
由正弦定理得
![]()
又![]()
![]() …………………………………………………………12分
…………………………………………………………12分
22.(1)![]()
(2) ![]()
(3)![]()