高三数学第一学期期中考试试题
一.选择题
1.若 (a－2i
) i
= b－i ,其中a、b∈R，i 是虚数单位,则 a 2 + b 2等于( )
A. 0 B.
2 C. 5 D.
2.在
的展开式中，
的系数为(
).
A.297 B.207 C.252 D.-45
3.在曲线
上的某点A处作一切线使之与曲线及
轴所围成图形的面积为
, 则切线方程为( )
A.
B.
C.
D.
4.坐标平面内向量
与轴正向上的单位向量
，满足
，则有(
)
A.
B.
C.或 D.
5.已知命题p:方程
有负根；命题q:方程
无实数根
若“p或q”为真命题，“p且q”为假命题，实数m的取值范围是( )
A.
B.
C.
D
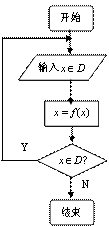6.设数列
是首项为
，公比为
的等比数列,
是数列的前
项和,
对任意的
N*，点
都在直线
上，则直线的方程是( )
A.
B.
C.
D.
7.对于任意函数
,构造一个数列发生器，其算法如右图所示，
现定义
，
,若输入初始值
,则当发生器结
束工作时,总共输入的数据个数为( )
A.8个 B.9个 C.10个 D.11个
8.已知二面角α—l—β的平面角为θ，PA⊥α,PB⊥β，A、B为垂足，
且PA=4，PB=5，点A、B到棱l的距离分别为x、y，当θ变化时，
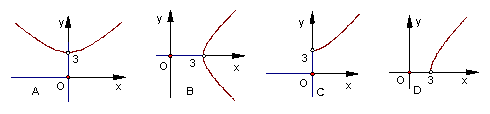点(x，y)的轨迹是下列图形中的( )
二.填空题
9.函数y=
的值域是
10.某人在黑暗中用6把钥匙随机开门，其中只有一把钥匙能把门打开，则他在三次内
(含3次)把门打开的概率是 .
11.将函数
的图象上每一点的纵坐标不变,横坐标变为原来的
倍,得到
图象C，若将的图象向上平移2个单位，也得到图象C，则
_
12.一个正方形被分成九个相等的小正方形,将中间的
一个正方形挖去(如图(1))；再将剩余的每个正方形
都分成九个相等的小正方形，并将中间一个挖去，
得图(2)；如此继续下去……，
试问第n个图共挖去 个正方形．
▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分
13.在极坐标系中,O是极点，设点A(4,
)，B(5,
)，则△OAB的面积是
.
14.若关于x的不等式
的解集不是空集，则a的取值范围是
.
15.在
中,
分别是角
的对边, 已知
,
,作
关于
的对称点
, 则
的最大值是
三.解答题
16.分别是中角A、B、C的对边，其外接圆半径为1，且
，边
是关于x的方程：
的两根(
)
(1)求
的度数及边的值;
(2)判定的形状，并求其内切圆的半径.
17.下表为某班英语及数学成绩的分布．学生共有50人，成绩分1—5五个档次．例如表
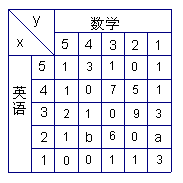中所示英语成绩为4分,数学成绩为2分的学生为5人．将全班学生的姓名卡片混在一起，任取一枚，该卡片同学的英语成绩为x,数学成绩为y,设x、y为随机变量
(注：没有相同姓名的学生)
(1)x=1的概率为多少？x≥3且y=3的概率为多少？
(2)a+b等于多少？若y的期望为
，试确定a、b的值.
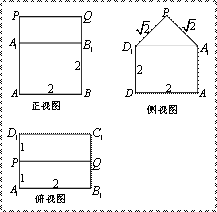18.如图，已知几何体的三视图(单位：cm)．
(1)画出这个几何体的直观图(不要求写画法)；
(2)求这个几何体的表面积及体积；
(3)设异面直线
、
所成角为
,求
.
19.设a>0，函数
(1)讨论f(x)的单调性；
(2)求f(x)在区间[a，2a]上的最小值.
20.已知椭圆
上任意一点P, 由P向x轴作垂线段PQ，垂足为Q，点M在线
段PQ上，且
，点M的轨迹为曲线E.
(1)求曲线E的方程；
(2)若过定点F(0，2)的直线交曲线E于不同的两点G，H(点G在点F，H之间),且满足
，求直线的方程.
21.已知函数
(1)求证：
为定值
(2)记
，求
(3)若函数
的图象与直线
以及轴所围成的封闭图形的面积为
，
试探究与的大小关系
答案
一.选择题: CBAD ADCD
二.填空题:
9.
; 10.
; 11.
; 12.
;
13.5; 14.
; 15.
三.解答题
16(1)
∵ b、c是的两根,且b>c 故b=2,c=1.
由余弦定理解得
，所以
.
(2)由
,
是直角三角形. 
17.(1)
(2)∵
……①，
又
∴
……②，
所以由①、②可得：
.
18.(1)这个几何体的直观图如图2－4所示．
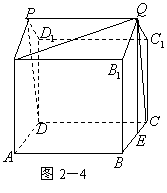(2)这个几何体可看成是由正方体
及直三棱柱
的组合体．
由
，
，可得
．
故所求几何体的全面积
所求几何体的体积
(3)由
，且
，可知
，
故
为异面直线、所成的角(或其补角).
由题设知
，
，
取
中点
，则
，且
，
．
由余弦定理，得
.
19(1)函数f(x)的定义域为
,对求导数得：
由
，得0<x<e， 由
，得x>e
故f(x)在(0,e)上单调递增，在(e,+∞)上单调递减.
(2)∵f(x)在(0,e)上单调递增，在(e,+∞)上单调递减.
∴f(x)在[a, 2a]上的最小值
∵
∴当
时，
；当a>2时，
20.(1)设M(x, y),
P(x0, y0), ∵, ∴
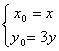, 将其代入
得
曲线E的方程为：
(2)设G(x1,
y1)、H(x2,
y2), ∵, ∴x2=2x1……①
依题意设直线l：
代入曲线E的方程并整理得
∴
……②，联立①②解得
所以直线l的方程为：y=
x+2.
21.(1)=3
(2)∵
, ∴
利用倒序相加可求得：
(3)∵
, 又由(1)知的图象关于点
中心对称，
∴
，
所以<.