高三数学第一学期调研测试试题
命题人:吴卫东、周德群、王康生、
黄春禄、张敏、丁凤桂等
注意事项:
1. 答卷前考生务必将自己的姓名、考号、考试科目填写在答题纸上,其中考号的涂写务必从左面第1列开始.
2. 交卷时,只交答题纸.
一、填空题:(每小题5分,14小题,共70分,把答案填在答题纸指定的横线上)
1.集合![]() ▲ .
▲ .
2.“![]() ”是“
”是“![]() ”的 ▲ 条件.
”的 ▲ 条件.
3.复数![]() 的值是 ▲ .
的值是 ▲ .
4.若向量![]() 的夹角为 ▲ .
的夹角为 ▲ .
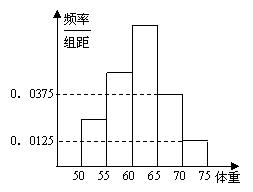 5.为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12,则抽取的男生人数是 ▲ .
5.为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12,则抽取的男生人数是 ▲ .
6.设![]() 、
、![]() 满足条件
满足条件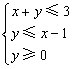 ,则
,则![]() 的最小值 ▲ .
的最小值 ▲ .
7.奇函数![]() 上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则
上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则![]() = ▲ .
= ▲ .
8.在![]() ABC中,
ABC中,![]() ,
,![]() ,面积为
,面积为![]() ,那么
,那么![]() 的长度为 ▲ .
的长度为 ▲ .
9.设等差数列![]() 的等比中项,则
的等比中项,则![]() 等于 ▲ .
等于 ▲ .
10.以下伪代码:
Read x
If x≤2 Then
y←2x-3
Else
y←log2x
End If
Print y
表示的函数表达式是 ▲ .
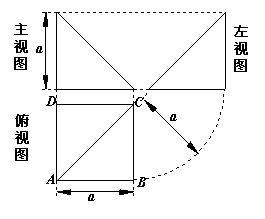
11.四棱锥![]() 的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
则四棱锥![]() 的表面积为 ▲ .
的表面积为 ▲ .
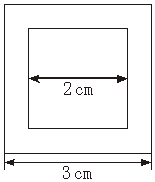
12.如下图,在一个边长为3 cm的正方形内部画一个边长为2 cm的正方形,向大正方形内随机投点,则所投的点落入小正方形内的概率是________.
13.设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转![]() 得到直线
得到直线![]() ,则
,则![]() 的方程是
的方程是
14.已知![]() 是不相等的两个正数,在
是不相等的两个正数,在![]() 之间插入两组数:
之间插入两组数:![]() 和
和![]() ,(
,( ![]() ,且
,且![]() ,使得
,使得![]()
![]() 成等差数列,
成等差数列,![]() 成等比数列.老师给出下列四个式子:①
成等比数列.老师给出下列四个式子:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ;⑤
;⑤![]() .其中一定成立的是 ▲ .(只需填序号)
.其中一定成立的是 ▲ .(只需填序号)
二、解答题:(本大题6小题,共90分,解答应写出文字说明、证明过程或演算步骤,并将解答过程写在指定的方框内)
15.(14分)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
| |
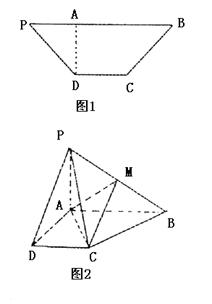
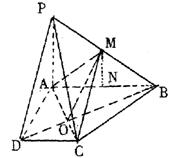
16.(15分)已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=![]() ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
(Ⅰ)证明:平面PAD⊥PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分![]() ;
;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD
是否平行面AMC.
17.(14分)已知过点A(0,1),且方向向量为![]() ,相交于M、N两点.
,相交于M、N两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() ;
;
(3)若O为坐标原点,且![]() .
.
18.(16分)设常数![]() ,函数
,函数![]()
![]() .
.
(1)令![]()
![]() ,求
,求![]() 的最小值,并比较
的最小值,并比较![]() 的最小值与零的大小;
的最小值与零的大小;
(2)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(3)求证:当![]() 时,恒有
时,恒有![]() .
.
19.(本小题满分15分)设函数![]() 求证:
求证:
(1)![]() ;
;
(2)函数![]() 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
(3)设![]() 是函数
是函数![]() 的两个零点,则
的两个零点,则![]()
20.(本题满分16分)设![]() 轴、
轴、![]() 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是![]() 、
、![]() ,坐标平面上点
,坐标平面上点![]() 、
、![]() 分别满足下列两个条件:①
分别满足下列两个条件:①![]() 且
且![]() ;②
;②![]() 且
且![]() .
.
(1)求![]() 及
及![]() 的坐标;
的坐标;
(2)若四边形![]() 的面积是
的面积是![]() ,求
,求![]() 的表达式;
的表达式;
(3)对于(Ⅱ)中的![]() ,是否存在最小的自然数M,对一切
,是否存在最小的自然数M,对一切![]() 都有
都有![]() 成立?若存在,求M;若不存在,说明理由.
成立?若存在,求M;若不存在,说明理由.
第Ⅱ部分 加试内容
(满分40分,答卷时间30分钟)
一、解答题:本大题共2小题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
1.求曲线![]() 与
与![]() 轴所围成的图形的面积.
轴所围成的图形的面积.
2.某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 | 4 | 5 |
|
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件![]() :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(2)求![]() 的分布列及期望
的分布列及期望![]() .
.
二、解答题:本大题共4小题,请从这4题中选做2小题,如果多做,则按所做的前两题记分.每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
3.(几何证明选讲)
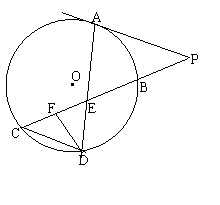 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE·EB=EF·EP;
(3)若CE : BE=3 : 2,DE=6,EF= 4,求PA的长.
4.(矩阵与变换)
已知曲线![]() :
:![]()
(1)将曲线![]() 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转![]() 后,求得到的曲线
后,求得到的曲线![]() 的方程;
的方程;
(2)求曲线![]() 的焦点坐标和渐近线方程.
的焦点坐标和渐近线方程.
5.(坐标系与参数方程)
已知直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() ,
,
(1)写出直线![]() 的参数方程;
的参数方程;
(2)设![]() 与圆
与圆![]() 相交与两点
相交与两点![]() ,求点
,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
6.(不等式选讲)
设a、b、c均为实数,求证:![]() +
+![]() +
+![]() ≥
≥![]() +
+![]() +
+![]() .
.
高三调研测试数学答案(08.1)
一.填空题:本大题共14小题,每小题5分,共70分.
1. {1,2,3} 2. 充分而不必要条件 3. 2 4. ![]() 5. 48 6. 4 7.
5. 48 6. 4 7.![]() 8.
8.![]()
9.4 10.![]() 11.
11.![]() 12.
12.![]() 13.
13.![]() 14.①②
14.①②
二..解答题:本大题共6小题,共90分.解答题应写出必要的计算步骤或推理过程.
15.解:(I)∵(2a-c)cosB=bcosC,
∴(2sinA-sinC)cosB=sinBcosC.……………………………………………2分
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA.…………………………………………4分
∵0<A<π,∴sinA≠0.
∴cosB=![]() .…………………………………………………………………5分
.…………………………………………………………………5分
∵0<B<π,∴B=![]() .…………………………………………………………6分
.…………………………………………………………6分
(II)![]() =4ksinA+cos2A.…………………………………………………………7分
=4ksinA+cos2A.…………………………………………………………7分
=-2sin2A+4ksinA+1,A∈(0,![]() )……………………………………10分
)……………………………………10分
设sinA=t,则t∈![]() .
.
则![]() =-2t2+4kt+1=-2(t-k)2+1+2k2,t∈
=-2t2+4kt+1=-2(t-k)2+1+2k2,t∈![]() .…………………………12分
.…………………………12分
∵k>1,∴t=1时,![]() 取最大值.
取最大值.
依题意得,-2+4k+1=5,∴k=![]() .……………………………………………………14分
.……………………………………………………14分
16.(I)证明:依题意知:![]()
|
![]() …4分
…4分
(II)由(I)知![]() 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD. …………5分
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则![]()
![]() …………8分
…………8分
要使![]()
即M为PB的中点. …………10分
(Ⅲ)连接BD交AC于O,因为AB//CD,AB=2,CD=1,由相似三角形易得BO=2OD
∴O不是BD的中心……………………10分
又∵M为PB的中点
∴在△PBD中,OM与PD不平行
∴OM所以直线与PD所在直线相交
又OM![]() 平面AMC
平面AMC
∴直线PD与平面AMC不平行.……………………15分
17解:(1)![]()
![]() ……………………2分
……………………2分
由![]()
![]() ……………………5分
……………………5分
![]()
![]() ……………………9分
……………………9分
![]()
![]()
![]() ……………………11分
……………………11分
![]() ……………………12
……………………12
![]()
![]()
![]() ……………………14分
……………………14分
18.解(Ⅰ)∵![]() ,
,![]()
∴![]() ,
,
![]() ……2分
……2分
∴![]() ,
,![]()
∴![]() ,令
,令![]() ,得
,得![]() ,
……4分
,
……4分
列表如下:
|
|
| 2 |
|
|
|
| 0 |
|
|
|
| 极小值 |
|
∴![]() 在
在![]() 处取得极小值
处取得极小值![]() ,
,
即![]() 的最小值为
的最小值为![]() . ……6分
. ……6分
![]() ,
,
∵![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() .
……8分
.
……8分
证明(Ⅱ)由(Ⅰ)知,![]() 的最小值是正数,
的最小值是正数,
∴对一切![]() ,恒有
,恒有![]() ,
……10分
,
……10分
从而当![]() 时,恒有
时,恒有![]() ,
……11分
,
……11分
故![]() 在
在![]() 上是增函数.
……12分
上是增函数.
……12分
证明(Ⅲ)由(Ⅱ)知:![]() 在
在![]() 上是增函数,
上是增函数,
∴当![]() 时,
时,![]() ,
……13分
,
……13分
又![]() ,
……14分
,
……14分
∴![]() ,即
,即![]() ,
……15分
,
……15分
∴![]()
故当![]() 时,恒有
时,恒有![]() .
……16分
.
……16分
19.证明:(1)![]()
![]()
又![]()
![]()
![]() ……………………2分
……………………2分
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0 ![]() ………………………………………………4分
………………………………………………4分
(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵a>0,∴f(0)=c>0且![]()
∴函数f(x)在区间(0,1)内至少有一个零点……………………8分
②当c≤0时,∵a>0 ![]()
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点…………………………10分
(3)∵x1,x2是函数f(x)的两个零点
则![]() 的两根
的两根
∴![]() ……………………………………12分
……………………………………12分
![]()
![]()
![]() ……………………………………15分
……………………………………15分
20.(本小题满分16分)
解:(1)![]()
![]()
![]()
![]()
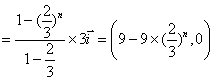 .……………………………………5分
.……………………………………5分
(2)![]()
![]() ,……………………………………………………10分
,……………………………………………………10分
(3)![]()
![]()
![]() 等
等
即在数列![]() 中,
中,![]() 是数列的最大项,所以存在最小的自然数
是数列的最大项,所以存在最小的自然数![]()
![]() ,对一切
,对一切![]() 都有
都有![]() <M成立. …………………………16分
<M成立. …………………………16分
第Ⅱ部分 加试内容
一、解答题:本大题共2小题,每小题10分,共20分.
1. 解 函数![]() 的零点:
的零点:![]() ,
,![]() ,
,![]() .…………………4分
.…………………4分
又易判断出在![]() 内,图形在
内,图形在![]() 轴下方,在
轴下方,在![]() 内,图形在
内,图形在![]() 轴上方,
轴上方,
所以所求面积为![]()
![]()
![]() ………10分
………10分
2. 解 (1)由![]() 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
知![]() 表示事件“购买该商品的3位顾客中无人采用1期付款”
表示事件“购买该商品的3位顾客中无人采用1期付款”
![]() ,
,![]() .…………4分
.…………4分
(2)![]() 的可能取值为
的可能取值为![]() 元,
元,![]() 元,
元,![]() 元.
元.
![]() ,
,![]() ,
,
![]() .
.
![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]()
![]() (元).……………………10分
(元).……………………10分
二、解答题:本大题共4小题,请从这4题中选做2小题,如果多做,则按所做的前两题记分.每小题10分,共20分.
3.
解 (1)∵DE2=EF·EC,
∴DE : CE=EF: ED.
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.……………………3分
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF·EP=DE·EA.
∵弦AD、BC相交于点E,∴DE·EA=CE·EB.∴CE·EB=EF·EP.………6分
(3)∵DE2=EF·EC,DE=6,EF= 4, ∴EC=9.
∵CE : BE=3 : 2, ∴BE=6.
∵CE·EB=EF·EP,∴9×6=4×EP.解得:EP=![]() .
.
∴PB=PE-BE=![]() , PC=PE+EC=
, PC=PE+EC=![]() .
.
由切割线定理得:PA2=PB·PC,
∴PA2=![]() ×
×![]() .∴PA=
.∴PA=![]() .……………………10分
.……………………10分
4. 解 (1)由题设条件,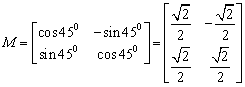 ,
,
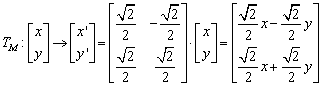 ,即有
,即有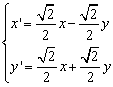 ,
,
解得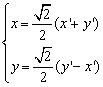 ,代入曲线
,代入曲线![]() 的方程为
的方程为![]() 。
。
所以将曲线![]() 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转![]() 后,得到的曲线是
后,得到的曲线是![]() 。………5分
。………5分
(2)由(1)知,只须把曲线![]() 的焦点、渐近线绕坐标原点顺时针旋转
的焦点、渐近线绕坐标原点顺时针旋转![]() 后,即可得到曲线
后,即可得到曲线![]() 的焦点坐标和渐近线方程。
的焦点坐标和渐近线方程。
曲线![]() 的焦点坐标是
的焦点坐标是![]() ,渐近线方程
,渐近线方程![]() ,
,
变换矩阵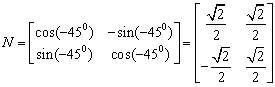
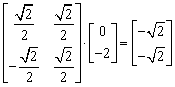 ,
,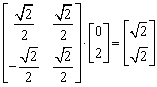 ,
,
即曲线![]() 的焦点坐标是
的焦点坐标是![]() 。而把直线
。而把直线![]() 要原点顺时针旋转
要原点顺时针旋转![]() 恰为
恰为![]() 轴与
轴与![]() 轴,因此曲线
轴,因此曲线![]() 的渐近线方程为
的渐近线方程为![]() 和
和![]() 。……………………10分
。……………………10分
5. 解 (1)直线的参数方程为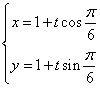 ,即
,即 .………………5分
.………………5分
(2)把直线 代入
代入![]() ,
,
得![]() ,
,![]() ,
,
则点![]() 到
到![]() 两点的距离之积为
两点的距离之积为![]() .……………………10分
.……………………10分
6. 证明: ∵a、b、c均为实数,
∴![]() (
(![]() +
+![]() )≥
)≥![]() ≥
≥![]() ,当a=b时等号成立;……………………4分
,当a=b时等号成立;……………………4分
![]() (
(![]() +
+![]() )≥
)≥![]() ≥
≥![]() ,当b=c时等号成立;……………………6分
,当b=c时等号成立;……………………6分
![]() (
(![]() +
+![]() )≥
)≥![]() ≥
≥![]() .……………………8分
.……………………8分
三个不等式相加即得![]() +
+![]() +
+![]() ≥
≥![]() +
+![]() +
+![]() ,
,
当且仅当a=b=c时等号成立. ……………………10分
(若有不同解法,请相应给分)