高三数学（文科）第一学期期中考试试卷
班级 姓名 学号 成绩
| 命题人 | 杨学东，张欣之，陈鸿霞 | 复核人 | 刘淼,袁野，任子中 | 教研组长 | 李欣 |
一、选择题:（每小题5分,共40分.请将答案填在第二页的表格中）
1．满足条件
的集合
的个数是（ ）
1
2
3
4
2．已知函数
，其中
，则
的值为（ ）
2
4
6
7
3．函数
是偶函数，且在区间
上单调递减，则
与
的大小关系为（ ）
不能确定
4．已知数列
是等差数列，数列
是等比数列，其公比
，且
（
），若
，
,则（ ）
或
5．数列、满足
，
，则的前10项之和等于（ ）
1
6．对于函数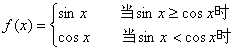
，下列结论正确的是（ ）
函数
的值域是［－1，1］
当且仅当
时，取最大值1
函数是以
为最小正周期的周期函数
当且仅当
（
）时，
7．若向量
，
则
与
满足（ ）
与的夹角等于
8．已知函数和
，对任意实数
有
，
，且当
时，
,
,则当
时（ ）
, ,
,
,
二．填空题（每题5分，共30分，请将答案填在第二页表中）
9．已知命题：“非空集合的元素都是集合
的元素”是假命题，则下列命题：
①的元素都不是的元素 ②的元素不都是的元素
③中有的元素
④存在
，使得
其中真命题的序号是 （将你认为正确的命题的序号都填上）
| 1 | 2 | |||
|
| 1 | |||
|
| ||||
|
| ||||
|
|
10．已知函数是
上的减函数，其图象经过点
和
，函数的反函数是
，则
的值为 ，不等式
的解集为
11．在如图的表格中，每格填上一个数字，使每一横行成等差数列，每一纵列成等比数列，则
12．已知
中，角
，
，
所对的边分别为
，
，
，若
，
，的面积为2，则的外接圆直径等于
13．已知
，函数
在
上是单调增函数，则的最大值是
14．函数是定义在
上的函数，满足
，且
，在每一个区间
（）上，
的图象都是斜率为同一常数
的直线的一部分，记直线
，
,轴及函数的图象围成的梯形面积为
（
），则数列的通项公式为
答案
1. 选择题
| 题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| 答案 |
2. 填空题
9. ; 10. ;
11. ; 12. ;
13. ; 14. .
2
班级 姓名 学号 成绩
三．解答题（共80分）
15．（12分）已知函数
，
，且
，若对任意
，都有
成立，求
的值
16．（12分）解关于的不等式
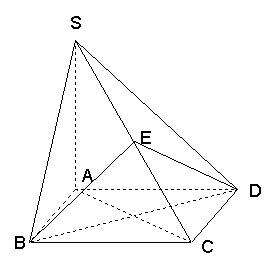
17．（14分）如图，四棱锥
的底面是正方形，
底面
，
是
上一点
（1）求证：平面
平面
；
（2）设
，
，求点到平面
的距离；
（3）当
的值为多少时，二面角
的大小为
3
班级 姓名 学号 成绩
18．（14分）数列中，
，且点
在直线
上
(1) 设
，求证：数列是等比数列；
(2) 设
，求数列
的通项公式；
(3) 求数列的前
项和
19．（14分）已知
，
（1）求导数
；
（2）若
，
（3）求函数在
上的最大值和最小值；
（4）若在
和
上都是单调递增的，
（5）求的取值范围
4
班级 姓名 学号 成绩
20．（14分）如果一个数列的各项的倒数成等差数列，我们把这个数列叫做调和数列
(1)若
，
，
成等差数列，证明
，
，
成调和数列；
(2)设是调和数列
的前项和，证明对于任意给定的实数
，总可以找到一个正整数
，使得当
时，
高三数学答案（文科）
一. 选择题
| 题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| 答案 | D | D | C | B | B | C | B | B |
二. 填空题
9. ②④ ; 10. -4
, (-2,2) ;11. 1 ;
12.
; 13.3; 14.
三．解答题
15．解：依题意
由
得
16．解：原不等式等价于
当
时，解集为
当
时，解集为
当
时，解集为
当
时，解集为
当
时，解集为
17．(1)证明：
底面
且
平面平面
(2)解：因为
，且
，
可求得点到平面的距离为
(3)解：作
，连
，则
为二面角
的平面角
设
，
，在
中，求得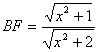
，
同理，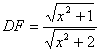
，由余弦定理
解得
， 即
＝1时，二面角的大小为
18．（1）证明：由已知得
，
即
，所以数列
是等比数列
（2）解：
，
，
（3）解：
设
所以
所以
19．解：（1）
（2）由
得
，所以
令
，得
或－1，
，
，
所以在
上的最大值为
，最小值为
（3）依题意只须
，
,
即
，解得的取值范围为［－２，２］
20.证明：（１）欲证
，，成调和数列，
只须证
只须证
化简后，只须证
因为
，
，成等差数列，所以成立
所以，，成调和数列
（２）
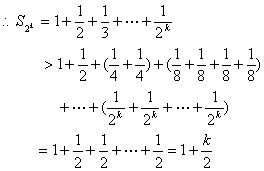
对于任一给定的，欲使
，只须
，即
，
取
(其中
表示
的整数部分)，则当
时，
(本题解法和答案不唯一)