高三文科数学12月月考试卷
高三数学(文科)
命题人:张宏汉 审题人:杨红云
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 共150分,考试时间120分钟. http://www.mathedu.cn
注意事项:
1.第Ⅰ卷的答案用2B铅笔涂在答题卡上,第Ⅱ卷的答案或解答过程均写在答题纸内的指定处,写在试题卷上的无效.
2.答题前,考生务必将自己的“班级”、“学号”、“姓名”写在答题卡和答题纸上.
3.考试结束后,只交答题卡和答题纸.
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则A![]() (CUB)= ( )
(CUB)= ( )
A. {2} B. {2,3} C. {1,3} D. {3}
2.已知![]() ,且
,且![]() ,则
,则![]()
![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.等差数列![]() 的公差为2,若a1、a3、a4成等比数列,则a2= (
)
的公差为2,若a1、a3、a4成等比数列,则a2= (
)
A.-6 B.-8 C.8 D.6
4.设b、c表示两条直线,![]() 、β表示两个平面,下列命题中真命题是 ( )
、β表示两个平面,下列命题中真命题是 ( )
A.若b![]()
![]() ,c∥
,c∥![]() ,则b∥c. B.若b
,则b∥c. B.若b![]()
![]() ,b∥c,则c∥
,b∥c,则c∥![]() .
.
C.若c∥![]() ,c⊥β,则
,c⊥β,则![]() ⊥β. D.若c∥
⊥β. D.若c∥![]() ,
,![]() ⊥β,则c⊥β
⊥β,则c⊥β
5.已知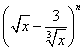 展开式中,各项系数的和为64,则
展开式中,各项系数的和为64,则![]() 等于 ( )
等于 ( )
A. 7 B. 6 C. 5 D. 4
6.![]() 的图象相邻两对称轴之间的距离为 (
)
的图象相邻两对称轴之间的距离为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
7.某小组有4名男生,5名女生,从中选派5人参加竞赛,要求有女生且女生人数少于男生人数的选派方法种数有 ( )
A. 40 B. 45 C. 105 D. 110
8.设三棱锥的3个侧面两两互相垂直,且侧棱长均为![]() ,则其外接球的表面积为 ( )
,则其外接球的表面积为 ( )
A.![]() B.
B.
![]() C.
C. ![]() D.
D.![]()
9.已知直线![]() 按向量
按向量![]() 平移后得到的直线
平移后得到的直线![]() 与圆
与圆![]() 相切,那么
相切,那么![]() 的值为
( )
的值为
( )
A.9或-1 B.5或-5 C.-7或7 D.-1或9
10.已知抛物线![]() 的准线与双曲线
的准线与双曲线![]() 的一条准线重合,则这条抛物线
的一条准线重合,则这条抛物线![]() 与双曲线
与双曲线![]() 的交点P到抛物线焦点的距离为
( )
的交点P到抛物线焦点的距离为
( )
A.![]() B.21 C.6
D.4
B.21 C.6
D.4
11.已知![]() 是定义在R上的奇函数,且是周期为2的周期函数,当
是定义在R上的奇函数,且是周期为2的周期函数,当![]() 时,
时, ![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.-5 C.
B.-5 C.![]() D.-6
D.-6
12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() ,例如,明文
,例如,明文![]() 对应密文
对应密文![]() .当接收方收到密文
.当接收方收到密文![]() 时,则解密得到的明文为 ( )
时,则解密得到的明文为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
高三文科数学12月月考试卷
![]() 高三数学(文科)
高三数学(文科)
| 题 号 | 一 | 二 | 三 | 总分 |
| 得 分 |
|
|
|
|

二、填空题:本大题共4小题,每小题5分,共20分。把答案填在题中相应的横线上
13.实践中常采用“捉-放-捉”的方法估计一个鱼塘中鱼的数量。如从这个鱼塘中随机捕捞出100条鱼,将这100条鱼分别作一记号后再放回鱼塘,数天后再从鱼塘中随机捕捞出108条鱼,其中有记号的鱼有9条,从而可以估计鱼塘中的鱼有 条。
14.设![]() ,
,![]() 为正数 ,则
为正数 ,则![]() 的最小值是 .
的最小值是 .
15.若不等式![]() 无解,则
无解,则![]() 的取值范围是
.
的取值范围是
.
16.函数![]() 是定义在R上的奇函数,给出下列命题:①
是定义在R上的奇函数,给出下列命题:①![]() =0, ②若
=0, ②若![]() 在
在![]() 上有最小值为-1,则
上有最小值为-1,则![]() 在
在![]() 上有最大值1;③若
上有最大值1;③若![]() 在
在![]() 上为增函数,则
上为增函数,则![]() 在
在![]() 上为减函数;④若x>0,
上为减函数;④若x>0,![]() =x2-2x;则x<0时,
=x2-2x;则x<0时,![]() =-x2-2x.
=-x2-2x.
其中所有正确的命题序号是______________ .
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
17. (本大题满分10分) 某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4
次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考
 到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8, 0.9。
到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8, 0.9。
(1)求在一年内李明第二次领到驾照的概率;
(2)求李明在一年内领到驾照的概率.
18.(本题满分10分)
设函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,的对边,![]()
 求b,c的长.
求b,c的长.

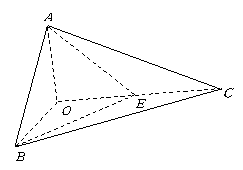 19.(本题满分12分) 如图,已知三棱锥
19.(本题满分12分) 如图,已知三棱锥![]() 的侧棱
的侧棱![]() 两两垂直,且
两两垂直,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求![]() 点到面
点到面![]() 的距离;
的距离;
(2)求异面直线![]() 与
与![]() 所成的角.
所成的角.
20.(本题满分12分) 数列![]() 的前
的前![]() 项和记为
项和记为![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
 (Ⅱ)等差数列
(Ⅱ)等差数列![]() 的各项为正,其前
的各项为正,其前![]() 项和为
项和为![]() ,且
,且![]() ,又
,又![]() 成等比数列,求
成等比数列,求![]() .
.
 21.(本题满分12分).已知函数f(x)=2x3+ax与g(x)=bx2+c的图像都过P(2,0),且在点P处有相同的切线.
21.(本题满分12分).已知函数f(x)=2x3+ax与g(x)=bx2+c的图像都过P(2,0),且在点P处有相同的切线.
(1)求实数a、b、c的值.
(2)设函数F(x)=f(x)+g(x),求F(x)的单调区间.
22.(本题满分14分).已知斜率![]() 的直线
的直线![]() 过椭圆C:
过椭圆C:![]() 的焦点以及点(0,
的焦点以及点(0,![]() ),椭圆C的中心关于直线
),椭圆C的中心关于直线![]() 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
 ⑵是否存在过点E(-2,0)的直线
⑵是否存在过点E(-2,0)的直线![]() 交椭圆C于点M、N,使△MON的面积为
交椭圆C于点M、N,使△MON的面积为![]() ,(O为坐标原点)?若存在,求出直线
,(O为坐标原点)?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
高三数学12月月考答案(文科)
选择题答案:CBACB ABBAD CC
填空题答案:13.1200 14.9 15. ![]() 16.①②④
16.①②④
解答题答案:
17解:(1).李明第一次参加驾照考试就通过的概率是P1=0.6.
李明在第一次考试未通过,第二次考试通过的概率
![]() ……………………(5分)
……………………(5分)
(2)李明在一年内领到驾照的概率为
1-(1-0.6)(1-0.7)(1-0.8)(1-0.9)=0.9976.……………………(10分)
18、解(Ⅰ)![]()
![]()
![]() ……………………(3分)
……………………(3分)
∴![]() …………………(5分)
…………………(5分)
(Ⅱ)f (A) = 2 即![]() …………………(7分)
…………………(7分)
![]()
∴b2 + c2-bc = 3 ①
又b2 + c2 + 2bc = 9 ②
②-① bc = 2 ③
b + c = 3 ④
b > c ⑤
由③,④解出![]() ……………………(10分)
……………………(10分)
19.解析:.(1)取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]()
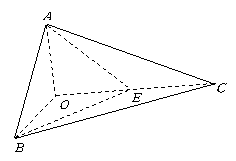
![]() 、
、![]()
![]() ……(2分)
……(2分)
则![]() 面
面![]() ,
,![]() 的长就是所要求的距离.
的长就是所要求的距离.![]()
![]() 、
、![]() ,
,
![]() ………(2分)
………(2分)
![]() ,在直角三角形
,在直角三角形![]() 中,有
中,有![]() …………………………(6分)
…………………………(6分)
(另解:由![]()
(2)取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]() ,则
,则![]() ∥
∥![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角. …………………………(8分)
所成的角. …………………………(8分)
求得: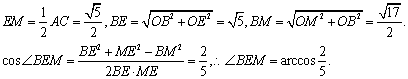 …………(12分)
…………(12分)
方法二:(1)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则有![]() 、
、![]() 、
、![]() 、
、![]()
设平面![]() 的法向量为
的法向量为![]()
则由![]()
由![]()
![]() ,则点
,则点![]() 到面
到面![]() 的距离为
的距离为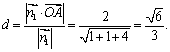 ………………(6分)
………………(6分)
![]()
![]() <
<![]() >
>![]() 所以异面直线
所以异面直线![]() 与
与![]() 所成的角
所成的角![]() .…………………………(12分)
.…………………………(12分)
20.解:(Ⅰ)由![]() 可得
可得![]() ,两式相减得
,两式相减得![]() ………………(2分)
………………(2分)
又![]() ∴
∴![]() ………………(4分)
………………(4分)
故![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 得等比数列∴
得等比数列∴![]() ………(6分)
………(6分)
(Ⅱ)设![]() 的公比为
的公比为![]()
由![]() 得,可得
得,可得![]() ,可得
,可得![]() ………………(8分)
………………(8分)
故可设![]()
又![]()
由题意可得![]() ………………(10分)
………………(10分)
解得![]()
∵等差数列![]() 的各项为正,∴
的各项为正,∴![]()
∴![]()
∴ ![]() ………………(12分)
………………(12分)
21、解:(1)∵f(x),g(x)的图像过P(2,0)
∴f(2)=0即2×23+a×2=0 a=-8…………………………………………(2分)
g(2)=0 即:4×b+c=0……………………………………………………(4分)
又∵f(x),g(x)在P处有相同的切线
∴4b=16 b=4 c=-16
∴a=-18 b=4 c=-16……………………………………………………(6分)
(2)F(x)=2x3+4x2-8x-16
F′(x)=6x2+8x-8
解不等式F′(x)=6x2+8x-8≥0得
x≤-2或x≥![]() 即单调增区间为
即单调增区间为![]() …………………………(9分)
…………………………(9分)
同理,由F′(x)≤0得
-2≤x≤![]() ,即单调减区间为[-2,
,即单调减区间为[-2,![]() ]……………………………………(12分)
]……………………………………(12分)
22 ⑴直线![]() ①,过原点垂直于
①,过原点垂直于![]() 的直线方程为
的直线方程为![]() ②
②
解①②得![]() .
.
∵椭圆中心O(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴![]() , ………(3分)
, ………(3分)
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0),
过椭圆焦点,∴该焦点坐标为(2,0),
∴![]() ,故椭圆C的方程为
,故椭圆C的方程为![]() ③……………(6分)
③……………(6分)
⑵当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 代入③并整理得
代入③并整理得
![]() ,
,
设![]() ,则
,则![]() …………………(8分)
…………………(8分)
∴![]() ,………(10分)
,………(10分)
点![]() 到直线
到直线![]() 的距离
的距离 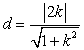 , ……………………………………(11分)
, ……………………………………(11分)
∵![]() , ∴
, ∴![]() ,即
,即![]()
解得 ![]() ,此时
,此时![]() …………………………………(13分)
…………………………………(13分)
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,也有
,也有![]()
故存在直线![]() 满足题意,其方程为
满足题意,其方程为![]() .……………(14分)
.……………(14分)