高三文科数学上学期年级期末考试
命题人：肖安平 审题人：林春保
注意事项：
1．答卷前，考生务必将自己的姓名、考号、学校写在答题纸的密封线内。
2．选择题的每小题选出答案后，把答案代码填在答题纸前面的选择题答题表内，不
能答在试卷上。
3．填空题和解答题应在指定的地方作答，否则答案无效。
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有
一项是符合题目要求的．
1．已知全集 I ＝{1，2，3，4}，A ＝{1}，B ＝{2，4}，则 A∪(
IB)＝
A．{1} B．{3} C．{1，2，4} D．{1，3}
2．已知甲：a ＞ b，乙：a3＞ b3，则甲是乙成立的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．正方体的截面不可能是
①锐角三角形；②直角三角形；③钝角三角形；④菱形；⑤正五边形；
⑥正六边形
A．①④⑤ B．②③⑤ C．②③⑥ D．②④⑤
4．已知：l1：(2a ＋5) x ＋( a －2) y ＋4＝0和 l2：(2－ a ) x ＋( a ＋3) y －1＝0互相垂
直，则 a 的值为
A．－2 B．－2或2 C．2 D．－2或2或－3
5．已知函数 f (x)＝2sin
(3x ＋ j ), 若 f (a)＝2, 则 f ( a ＋ 
)与
f ( a ＋ 
)的大小关系是
A．f ( a ＋ 
)＜
f ( a ＋ )
B．f ( a
＋ )＞
f ( a ＋ )
C．f ( a ＋ )＝
f ( a ＋ )
D．与 j 和 a 有关
6．数列{a 
}中，a ＝2且 a 
＝
(a
＋
a ＋…＋a )，记
S 为数列{a }的前
n 项和,
则 Sn 等于
A．4( 
)n－4
B．2·( )n C．2·( )n－1 D．4( )n－2
7．我国发射的“神舟五号”载人飞船的运行轨道是以地球的中心为一个焦点的椭
圆，近地点距地面为 m (km)，远地点距地面 n (km)，地球半径为 R (km)，则飞船
运行的轨道的短轴长为
A．2 
B．
C．mn D．2mn
8．设 
、
是平面直角坐标系内分别与
x 轴、y 轴方向相同的两个单位向量，且 
＝4 ＋2 ，
＝3 ＋4 ，则△OAB 的面积等于
A．15 B．10 C．7.5 D．5
9．如图，正四面体 ABCD 为棱长均为8，E、F 分别为 AD、
BC 上一点，且 AE ＝2，BF ＝1，则 EF 的长为
A．3 B．
C．3 D．4
10．函数 f (x)＝ x ＋ 
，则其反函数的定义域为
A．[－2
，2 ] B．[－2，2]
C．[－2 ，2] D．以上均不对
二、填空题：（本大题共5小题，每小题5分，共25分）
11．已知 bn＝ lgan，数列{bn}是首项为 lg2，公差为 lg3的等差数列，则 a1＋ a2＋ a3＋
a4＝____________．
12．已知双曲线的焦点到渐近线的距离等于右焦点到右顶点的距离的2倍。则此双曲
线的离心率 e ＝____________．
13．已知 f (x)是以2为周期的偶函数，当 x ∈[0，1]时，f (x)＝ x，若在区间[－1，3]
内，关于 x 的方程 f (x)＝ kx ＋ k ＋1( k∈ R 且 k ≠－1)有四个不等的实根，则 k 的
取值范围是____________．
14．设 x、y ∈ R，x＋y≤2，Z －2x ＋ y ＝0，则 Z 的最大值为____________．
15．一个正整数数表如下（表中下一行的数的个数是上一行中数的个数的2倍）
| 第1行 | 1 |
| 第2行 | 2 3 |
| 第3行 | 4 5 6 7 |
| …… | …… |
则第10行中的第5个数是____________．
三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤。
16．（本小题满分12分）
已知 
＝( cosx，sinx )，
＝1，且 与
满足 k ＋
＝
－k ( k
＞0)．
(1)试用 k 表示 ·，并求
·的最小值；
(2)若0≤ x ≤ p，＝( ，
)，求
x 值使 ·取值大值．
17．（本小题满分12分）
已知函数 f (x)在 R 上是增函数，a、b ∈R
⑴求证：如果 a ＋ b ≥0，那么 f (a)＋ f (b)≥ f (－a )＋ f (－b )；
⑵判断(1)中的命题的逆命题是否成立，并证明你的结论；
再解不等式：f ( lg 
)＋
f (2)≥ f ( lg 
)＋
f (－2)
18．（本小题满分12分）
在三棱锥 V － ABC 中，底面△ABC 是以∠B 为直角
的等腰三角形，又 V 在底面ABC 上的射影 H 在线段
AC 上且靠近点 C，AC ＝4，VA ＝ 
，VB 和底面
ABC所成的角为45o．
⑴求点 V 到底面 ABC 的距离；
⑵求二面角 V — AB — C 的正切值．
19．（本小题满分12分）
如图所示，过△AOB 的重心 G 的直线 PQ 与线段 OA、OB 分别交于 P、Q 点，若
＝l ，
＝m( 
) ( l、m＞0)，且△AOB 和
△POQ 的面积分别为 S、T．
⑴求证：
＋
为定值；
⑵试用 S 表示出 T 的取值范围．
20．（本小题满分13分）
已知直线 x ＋ y －1＝0与椭圆 
＋
＝1( a ＞ b ＞0)相交于 A、B 两点，M 是线
段 AB 上的一点，
＝－
，且点
M 在直线 l：y ＝
x 上．
⑴求椭圆的离心率；
⑵若椭圆的焦点关于直线 l 的对称点在单位圆 x2＋ y2＝1上，求椭圆的方程．
21．（本小题满分14分）
已知数列{an}的通项为
a ，前
n 项和为 Sn，且 an 是 Sn 与2的等差中项；数列{bn}
中，b1＝1，点 P ( bn，bn＋1)在直线 x － y ＋2＝0上．
⑴求数列{an}、{bn}的通项公式 an、bn；
⑵设{b }的前
n 项和为 B ，试比较
＋
＋…＋
与2的大小；
⑶设 T ＝
＋
＋…＋
，求满足
T ＜
c 的最小整数 c．
鄂州市2007—2008学年度上学期期末考试
高三数学（文史类）参考答案
一、选择题：
二、填空题：
11．80 12．
13．(－
，0) 14．4 15．516
三、解答题：
16．解：⑴∵( k ＋
)2＝3( －
k )2 ∴ k2＋1＋2 k
·
＝3(1＋ k2－2 k ·
) (3分)
∴ ·
＝
＝
( k
＋ 
)≥
，当且仅当
k ＝1时取等号
………(6分)
⑵ ·
＝
cosx ＋ 
sinx ＝ sin ( x＋ 
) …………………………… (9分)
∵0≤ x ≤ p ∴ 
≤
x ＋ ≤
∴当：x ＋ ＝
，即
x ＝ 
时，
·
取最大值1 …………………(12分)
17．解：⑴证明：当 a ＋ b ≥0时，a ≥－ b 且 b ≥－ a，∵ f (x)为 R 上的增函数
∴ f (a)≥ f (－b)， f (b)≥ f (－a)
∴ f (a)＋ f (b)≥ f (－a)＋ f (－b) ……………………………………… (4分)
⑵⑴中命题的逆命题为：如果 f (a)＋ f (b)≥ f (－a)＋ f (－b)，那么 a ＋ b ≥0
即 f (a)＋ f (b)≥ f (－a)＋
f (－b) 
a ＋ b ≥0
① ………………… (6分)
证明一：①的逆否命题是：a ＋ b ＜0 f (a)＋ f (b)＜ f (－a)＋ f (－b) ②
仿⑴的证明可证②成立，又①与②互为逆否命题，故①成立
证明二：用反证法(略) ………………………………………………… (8分)
由以上证明知 f (a)＋ f (b)≥ f (－a)＋
f (－b) 
a ＋ b ≥0
∴原不等式 lg 
＋2≥0 ≥
－1＜ x ≤ 
……………………………………………………………………………(11分)
∴不等式的解集为 
…………………………………(12分)
18．解：⑴∵V 在底面 ABC 上的射影 H 在线段 AC 上且靠近点 C
∴ VH ⊥底面 ABC，HA ＞ AC ＝2
又∵ VB 和底面 ABC 所成的角为45o
即∠ VBH ＝45o …………………………(2分)
设 VH ＝ x，则 HB ＝ x，HA ＝ 
在△ HAB 中，∠CAB ＝45o，AB ＝2 
，
由余弦定理知 HB2＝ HA2＋ AB2－2 HA·ABcos45o
即 x2＝14－ x2＋8－4 x4－18 x2＋65＝0 ( x2－13)( x2－5)＝0
又 HA ＝ ＞2 ∴0＜ x ＜
∴ x ＝ 
故点 V 到底面 ABC 的距离为
……………………………………(7分)
⑵过 H 作 HD ⊥ AB 于 D，连 VD，由三垂线定理知，∠VDH 即为二面角 V
－ AB － C 的平面角．∵
HA ＝3 ∴ HD ＝3sin45o＝ 
∴ tan ∠VDH
＝
＝
＝
…………………………………………………(12分)
19．⑴证明：方法1，连接 OG 并延长交 AB 于 M，
因为 P、G、Q 三点共线，所以存在非零实数 t ，
使 
＝
t 
，则
＝
t ( ＋
)
∴ ＝
，∴
－
＝
( －
)
∴ ＝(1－ t ) ＋
t 
，又
＝
，
＝ m 
∴ ＝(1－
t ) ＋ t m ………………………………(4分)
又 
＝
( ＋
)，＝
∴ ＝
( ＋
)
∴ ，从中消去参数
t 得 
＋
＝3
∴ ＋
为定值3． ………………………………………………………… (6分)
方法2：＝
( ＋
)，＝
∴ ＝
( ＋
)，又
＝
，＝
∴ ＝
，＝
，从而
＝
＋
，因为 P、G、Q 三点共线所以
＋
＝1，即 ＋
＝3
∴ ＋
为定值3．[参照方法1赋分]
⑵ 
＝
＝
＝
…………………………(8分)
由⑴知 ＝
，∴
＝
，∵0＜ 
≤1 ∴0＜ ≤1，解
之得 
≤
≤1
…………… (10分)
∵ ≤
≤1 ∴1≤ ≤2 从而2≤－( －
)2＋
≤
∴ 
≤
≤
，从而
S ≤ T ≤ S
∴用 S 表示出 T 的取值范围是[ S， S ] ………………………………(12分)
20．解：⑴由 
＝－
可知，M 是 AB 的中点，设 A ( x，y)，B ( x，y)
由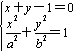 
( a2＋ b2) x2－2 a2＋ a2－ a2b2＝0
x＋ x＝ 
，y＋ y＝－( x＋ x)＋2＝ 
∴ M 点的坐标为( 
，
) ………………………………… (3分)
又∵ M 在直线 l∶y ＝ x上 ∴ ＝
· a2＝2 b2，从而
a2＝2 c2 ∴ 
＝
∴ e2＝ ，e ＝ 
………………………… (6分)
⑵由⑴知 b ＝ c，不妨设椭圆的一个焦点为 F ( b，0)，F ( b，0)关于直线
l∶y ＝ x 的对标点为( x，y)，则
解之得，
x＝ 
b ，y＝
b ……………………………………………………(10分)
由已知 x＋
y＝1，
∴( b)2＋( 
b)2＝1 b2＝1，从而得椭圆方程为 
＋
y2＝1 … (13分)
21．解：⑴由条件2 an＝ Sn＋2 ∴2 an＋1＝ Sn＋1＋2，两式相减得 an＋1＝2 an
∴ 
＝2，又 a＝ S＝2 a－2 ∴ a＝2
∴{an}是以2为首项，2为公比的等比数列∴ an＝2n ( n∈N*) ………(2分)
又∵ P ( b
，b
)在直线 x － y ＋2＝0上
∴ b－ b＝2，又 b＝1
∴{bn}是以1为首项，2为公差的等差数列 ∴ bn ＝2 n－1 ( n∈N*)
…………………………………………………………………………… (4分)
⑵∵ B＝1＋3＋5＋…＋2 n－1＝ n ∴ 
＝
＜
＝
－
( n
≥2) 从而 
＋
＋…＋
＜1＋ 
＋
＋…＋
＝1＋
(1－ )＋( －
)＋…＋( －
)＝2－ ＜2 ………………… (8分)
⑶ T＝
＋
＋…＋
＝
＋
＋
＋…＋
①
当 n ＝1时，T＝
当 n ≥2时， T＝
＋
＋
＋…＋
＋
②
①－②得 T＝
＋( ＋
＋…＋
)－
∴ T＝1＋(1＋ ＋…＋
)－
＝1＋ －
＝3－
－ ＜3
∵ T是递增的 ∴ T∈[ ，3]，又 T＝3－ －
＝
＞2
∴满足条件 T＜
c 的最小整数 c ＝3．……………………………… (14分)