高三数学(文科)统一练习一
(1)已知集合M={yy=2x,xÎR},P={yy=![]() },则MÇP是
},则MÇP是
(A) {yy>1} (B) {yy³1} (C) {yy>0} (D) Æ
(2)已知等差数列{an}中,a6+a10=16,a4=1,则a12的值是
(A) 15 (B) 30 (C) 31 (D) 64
(3) 把编号为1、2、3、4的4位运动员排在编号为1、2、3、4的4条跑道中,要求有且只有两位运动员的编号与其所在跑道的编号相同,共有不同的排法种数是
(A) 3 (B) 6 (C) 12 (D) 24
(4) 在底面是矩形的直四棱柱ABCD-A1B1C1D1中,∠DAD1=∠CDC1=45°,那么异面直线AD1与DC1所成角的度数为
(A) 30° (B) 45° (C) 60° (D) 90°
(5) 已知f(x)=logax,当x>1时,f(x)>0,则当0<m<1<n时,下列式子正确的是
(A) 0<f(m)<f(n) (B) f(m)<0<f(n) (C) f(n)<f(m)<0 (D) f(n)<0<f(m)
(6) “a+b=2”是“直线x+y=0与圆![]() 相切”的
相切”的
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
(7) 已知M(2,1),N(-1,2),在下列方程的曲线上,存在点P满足![]() 的曲线是
的曲线是
(A) 3x-y+1=0 (B)![]() (C)
(C) ![]() (D)
(D)![]()
(8)对任意两实数a、b,定义运算“![]() ”如下:
”如下:![]() 则关于函数f(x)=sinx
则关于函数f(x)=sinx![]() cosx正确的命题是
cosx正确的命题是
(A) 函数f(x)值域为[-1,1]
(B)当且仅当x=2k![]() (k
(k![]() 时,函数f(x)取得最大值1
时,函数f(x)取得最大值1
(C)函数f(x)的对称轴为x=![]() (k
(k![]()
(D)当且仅当2k![]() <x<2k
<x<2k![]() +
+![]() (k
(k![]() 时,函数f(x)<0
时,函数f(x)<0
二、填空题
(9) 在![]() 的展开式中,含
的展开式中,含![]() 与
与![]() 项的系数相等,则a的值是 。
项的系数相等,则a的值是 。![]()
(10) 已知向量![]() ,
,![]() 的夹角为
的夹角为![]() ,要使向量
,要使向量![]() 与
与![]() 垂直,则
垂直,则![]() = 。1
= 。1
(11) 已知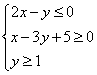 ,则z=x+y-2的最大值是
。1
,则z=x+y-2的最大值是
。1
(12) 若椭圆![]() 的左右焦点分别是
的左右焦点分别是![]() ,线段
,线段![]() 被y
被y![]() 焦点分为3:1两段,则此椭圆的离心率为
。
焦点分为3:1两段,则此椭圆的离心率为
。![]()
(13) 各棱长为a的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为
。![]()
(14) 二次函数y=![]() 的部分对应值如下表:
的部分对应值如下表:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| Y | 10 | 4 | 0 | -2 | -2 | 0 | 4 | 10 |
则不等式![]() 的解集是
。
的解集是
。![]()
三、解答题
15.(13分)已知向量![]() =(sin
=(sin![]() ,2cos
,2cos![]() ),
),![]() =(
=(![]() )
)
(Ⅰ)当qÎ[0,p]时,求函数f(![]() )=
)=![]() ×
×![]() 的值域;
的值域;
(Ⅱ)若![]() ∥
∥![]() ,求sin2
,求sin2![]() 的值。
的值。
解:(Ⅰ)由f(![]() )=
)=![]() ×
×![]() 得,
得,![]()
∵qÎ[0,p],![]()
∴![]() 的值域为[-1,2]
的值域为[-1,2]
(Ⅱ)∵![]() ∥
∥![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
16.(12分)袋中黑白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲、乙两人从袋中轮流摸取1球,规定甲先乙后,然后甲再取…,取后不放回,直到两人中有一人取到白球就终止,每个球在每次被摸出的机会均等。
,现有甲、乙两人从袋中轮流摸取1球,规定甲先乙后,然后甲再取…,取后不放回,直到两人中有一人取到白球就终止,每个球在每次被摸出的机会均等。
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求甲取到白球的概率。
解:(Ⅰ)设袋中原有白球n个,依题意有,![]() ,解得,n=3.
,解得,n=3.
所以,袋中原有白球的个数为3.
(Ⅱ)甲取到白球的事件可能发生在第1次、第3次、第5次,
所以甲取到白球的概率为![]() +
+![]() +
+![]() =
=![]() 。
。
17.(14分)已知四棱锥S-ABCD的底面ABCD是正方形,SA![]() 底面ABCD,点E是SC上的一点。
底面ABCD,点E是SC上的一点。
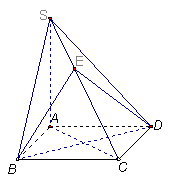 (Ⅰ)求证:平面EBD
(Ⅰ)求证:平面EBD![]() 平面SAC;
平面SAC;
(Ⅱ)设SA=4,AB=2,求点A到平面SBD的距离;
(Ⅲ)当SA=AB时,求二面角B-SC-D的大小。
解法一:
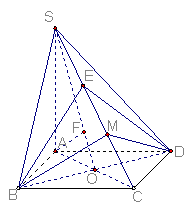 证明(Ⅰ):连结AC,∵ABCD是正方形,∴BD⊥AC, ∵ SA
证明(Ⅰ):连结AC,∵ABCD是正方形,∴BD⊥AC, ∵ SA![]() 底面ABCD,BDÌ面ABCD,∴SA
底面ABCD,BDÌ面ABCD,∴SA![]() BD,∵SAÇAC=A,∴BD^面SAC,又∵BDÌ面EBD,∴平面EBD
BD,∵SAÇAC=A,∴BD^面SAC,又∵BDÌ面EBD,∴平面EBD![]() 平面SAC
平面SAC
解(Ⅱ):由 (Ⅰ)知,BD^面SAC,又∵BDÌ面SBD,∴平面SBD![]() 平面SAC,
平面SAC,
设ACÇBD=O,则平面SBDÇ平面SAC=SO,过A作AF^SO交SO于点F,则AF^面SBD,所以线段AF的长就是点A到平面SBD的距离。
∵ABCD是正方形,AB=2,∴AO=![]() ,又∵SA=4,△SAO是Rt△,∴SO=
,又∵SA=4,△SAO是Rt△,∴SO=![]() ,
,
∵SO×AF=SA×AO,∴AF=![]() ,∴点A到平面SBD的距离为
,∴点A到平面SBD的距离为![]()
解(Ⅲ):作BM⊥SC于M,连结DM,∵SA![]() 底面ABCD,AB=AD,∴SB=SD,又∵CB⊥AB,CD⊥AD,∴CB⊥SB,CD⊥SD,∴△SBC≌△SDC,∴DM⊥SC,∴∠BMD是二面角B-SC-D的平面角,BM=DM. 在正方形ABCD中,设AB=a,则AC=BD=
底面ABCD,AB=AD,∴SB=SD,又∵CB⊥AB,CD⊥AD,∴CB⊥SB,CD⊥SD,∴△SBC≌△SDC,∴DM⊥SC,∴∠BMD是二面角B-SC-D的平面角,BM=DM. 在正方形ABCD中,设AB=a,则AC=BD=![]() a,∵AB=SA,∴SB=
a,∵AB=SA,∴SB=![]() a,SC=
a,SC=![]() a,∵BM×SC=SB×BC, ∴BM=
a,∵BM×SC=SB×BC, ∴BM=![]() a. ∴cos∠BMD=
a. ∴cos∠BMD=![]() ,∴二面角B-SC-D的大小为120
,∴二面角B-SC-D的大小为120![]() 。
。
解法二:
证明(Ⅰ)同解法一。
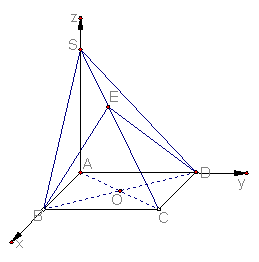
∵ABCD是正方形,SA![]() 底面ABCD,∴SA⊥AB,SA⊥AD,AB⊥AD,如图,建立直解坐标系A-xyz。
底面ABCD,∴SA⊥AB,SA⊥AD,AB⊥AD,如图,建立直解坐标系A-xyz。
(Ⅱ)A(0,0,0),B(2,0,0),D(0,2,0),S(0,0,4),设平面SBD的法向量为![]() ,则
,则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
 ∴
∴![]() ,
,![]() ,而
,而![]() =(2,0,-4),
=(2,0,-4),![]() =(0,2,-4)
=(0,2,-4)
∴![]() ,∴x=2,y=2,即
,∴x=2,y=2,即![]() ,则点A到平面SBD的距离d=
,则点A到平面SBD的距离d=![]() =
=![]()
(Ⅲ)设SA=AB=a,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),S(0,0,a);设平面SBC的法向量![]() =(x1,y1,-1),平面SDC的法向量
=(x1,y1,-1),平面SDC的法向量![]() =(x2,y2,1)
=(x2,y2,1)
则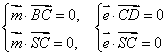 ,而
,而![]() =(0,a,0),
=(0,a,0),![]() =(-a,0,0),
=(-a,0,0),![]() =(a,a,-a)
=(a,a,-a)
∴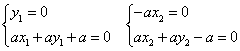 ,∴x1=-1,y1=0,x2=0,y2=1
,∴x1=-1,y1=0,x2=0,y2=1
∴![]() =(-1,0,-1),
=(-1,0,-1),![]() =(0, 1,1), ∴cos<
=(0, 1,1), ∴cos<![]() ,
,![]() >=
>=![]() =
=![]() ,∴二面角B-SC-D的大小为120
,∴二面角B-SC-D的大小为120![]() 。
。
18.(14分)已知定点F(1,0),动点P在y轴(不含原点)上运动,过点P作线段PM交x轴于点M,使![]() ;再延长线段MP到点N,使
;再延长线段MP到点N,使![]() 。
。
(Ⅰ)求动点N的轨迹C的方程;
(Ⅱ)直线L与轨迹C交于A、B两点,如果![]() =-4且
=-4且![]() ,求直线L的方程。
,求直线L的方程。
解:(Ⅰ)设N(x,y),P(0,p),由题意知,P为MN的中点,∴M(-x,2p-y),又M在x轴上,∴2p-y=0,即p=![]() ,∴P(0,
,∴P(0,![]() ),M(-x,0)
),M(-x,0)
∵![]() ,∴(-x,-
,∴(-x,-![]() )×(1,-
)×(1,-![]() )=0,∴y2=4x(x>0)
)=0,∴y2=4x(x>0)
∴动点N的轨迹C的方程为y2=4x(x>0)
(Ⅱ)若直线L的斜率不存在,设直线L的方程为x=a>0,此时,A(a,![]() ),B(a,
),B(a,![]() ),
), ![]() =a2-4a=-4,∴a=2,
=a2-4a=-4,∴a=2,![]() ,AB=
,AB=![]() ¹
¹![]() ,不符合题意,舍去。∴直线L的斜率存在。
,不符合题意,舍去。∴直线L的斜率存在。
设直线L的方程为y=kx+b,A![]() 、B
、B![]() ,
,
由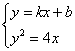 消去y整理得,ky2-4y+4b=0,△=16-16kb>0,y1+y2=
消去y整理得,ky2-4y+4b=0,△=16-16kb>0,y1+y2=![]() ,y1y2=
,y1y2=![]()
![]() =
=![]() =
=![]() =-4,∴b= -2k,∴y1y2=-8
=-4,∴b= -2k,∴y1y2=-8
AB=![]() =
=![]() =
=![]() ,
,
∵![]() ∴
∴![]()
![]() ∴k=±1 ∴当k=1时,b=-2,当k=-1时,b=2;所以直线L的方程为y=x-2或y=-x+2
∴k=±1 ∴当k=1时,b=-2,当k=-1时,b=2;所以直线L的方程为y=x-2或y=-x+2
(19)(14分)设函数![]() 的图象过点(-1,2)。
的图象过点(-1,2)。
(Ⅰ)试用a表示b;
(Ⅱ)当a=3时,求f(x)的单调区间与极值;
(Ⅲ)若a<0且f(-1)是函数f(x)的极小值,求a的取值范围。
解:(Ⅰ)∵函数![]() 的图象过点(-1,2),
的图象过点(-1,2),
∴![]() ,整理得,a-3b-12=0.
,整理得,a-3b-12=0.
(Ⅱ)当a=3时,由a-3b-12=0得,b=-3, ∴f(x)=x3-3x,![]() =3(x+1)(x-1),令
=3(x+1)(x-1),令![]() ,解得x1=-1,x2=1。当x变化时,
,解得x1=-1,x2=1。当x变化时,![]() ,f(x)的变化情况如下表:
,f(x)的变化情况如下表:
| x | (-¥,-1) | -1 | (-1,1) | 1 | (1,+¥) |
|
| + | 0 | - | 0 | + |
| f(x) |
| 极大值2 |
| 极小值-2 |
|
所以,f(x)的单调增区间是(-¥,-1),(1,+¥),单调减区间是(-1,1),极大值是f(-1)=2,极小值是f(1)=-2。
(Ⅲ)![]() =(x+1)(ax+b),∵a<0且f(-1)是函数f(x)的极小值,∴
=(x+1)(ax+b),∵a<0且f(-1)是函数f(x)的极小值,∴![]() >-1,又∵a-3b-12=0,∴
>-1,又∵a-3b-12=0,∴![]() ,∴
,∴![]() ,解得,a<-6,∴a的取值范围为(-¥,-6)
,解得,a<-6,∴a的取值范围为(-¥,-6)
(20)(13分)已知数列{![]() }满足
}满足![]() ,且
,且![]() 是
是![]() 的等差中项。
的等差中项。
(Ⅰ)求数列{![]() }的通项公式
}的通项公式![]() ;
;
(Ⅱ)若![]() =
=![]()
![]() ,求使S
,求使S![]() >50成立的正整数n的最小值。
>50成立的正整数n的最小值。
解:(Ⅰ)∵![]() ,即
,即![]() ,∴数列{
,∴数列{![]() }是以2为公比的等比数列。
}是以2为公比的等比数列。
∵![]() 是
是![]() 的等差中项,∴
的等差中项,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴数列{![]() }的通项公式
}的通项公式![]() 。
。
(Ⅱ)由(Ⅰ)及![]() =
=![]() 得,
得,![]() ,
,
∵![]() ,
,
∴![]() 1
1
∴![]() 2
2
2-1得,![]() =
=![]()
要使S![]() >50成立,只需2n+1-2>50成立,即2n+1>52,n³5
>50成立,只需2n+1-2>50成立,即2n+1>52,n³5
∴使S![]() >50成立的正整数n的最小值为5。
>50成立的正整数n的最小值为5。