高三理科数学素质测试
本卷分第一卷(选择题)和第二卷(非选择题)两部分,满分150分,考试时间120分钟。
第错误!未找到引用源。卷(选择题 共60分)
一、 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。请将答案填在答题卡相应位置。
(1) 已知向量![]() 满足
满足![]() 则
则![]() 夹角为
夹角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2) 已知![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3) 设i为虚数单位,复数![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4) 设点P是函数![]() 的图像C的一个对称中心,若点P到图像C的对称轴的距离的最小值是
的图像C的一个对称中心,若点P到图像C的对称轴的距离的最小值是![]() ,则
,则![]() 的最小正周期是
的最小正周期是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5) 点F为双曲线![]() 的右焦点,l为其右准线,l被双曲线的渐近线截得得线段长等于点F到直线l的距离,则双曲线的离心率为
的右焦点,l为其右准线,l被双曲线的渐近线截得得线段长等于点F到直线l的距离,则双曲线的离心率为
(A)![]() (B)
(B)![]() (C)2 (D)
(C)2 (D)![]()
(6) 在![]() 的展开式中,奇数项系数和为2048,则含x的正整数次幂的项共有
的展开式中,奇数项系数和为2048,则含x的正整数次幂的项共有
(A)4项 (B)3项 (C)2项 (D)1项
(7) 将4个颜色互不相同的球全部放入编号1和2的两个盒子里,使得放入每个盒子里球的个数不小于该盒子的编号,则不同的放法有
(A)10种 (B)20种 (C)30种 (D)52种
(8) 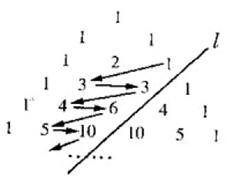 如图,在杨辉三角中,斜线l的上方从1开始按箭头所示的数组成一个锯齿形数列1,3,3,4,6,5,10,……,记此数列为
如图,在杨辉三角中,斜线l的上方从1开始按箭头所示的数组成一个锯齿形数列1,3,3,4,6,5,10,……,记此数列为![]() ,则
,则![]() 等于
等于
(A)55 (B)65 (C)66 (D)78
(9) 已知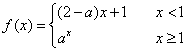 是R上的增函数,那么a的取值范围是
是R上的增函数,那么a的取值范围是
 (A)
(A)![]() (B)
(B)![]() (C)(1,2) (D)
(C)(1,2) (D)![]()
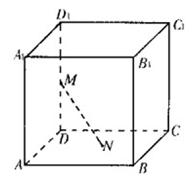
(10) 如图,已知正方形![]() 的棱长为2,长为2的线段MN的一个端点M在棱
的棱长为2,长为2的线段MN的一个端点M在棱![]() 上运动,点N在正方形ABCD内运动,则MN中点的轨迹的面积是
上运动,点N在正方形ABCD内运动,则MN中点的轨迹的面积是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11) 函数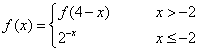 在
在![]() 上为增函数,
上为增函数,![]() 的最小值为
的最小值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(12) 设点O为![]() 所在平面内一点,且
所在平面内一点,且![]() ,则O一定为
,则O一定为![]() 的
的
(A)外心 (B)内心 (C)垂心 (D)重心
第错误!未找到引用源。卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。
(13) 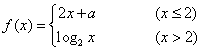 ,若
,若![]() 存在,则常熟a=______。
存在,则常熟a=______。
(14) 定义在R上的函数![]() ,对于人意实数x,都有
,对于人意实数x,都有![]()
(15) 已知实数x,y满足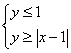 ,则x+2y的最大值是______。
,则x+2y的最大值是______。
(16) 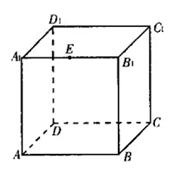 如图,正方体
如图,正方体![]() 的棱长为1,E为
的棱长为1,E为![]() 的中点。则下列五个命题
的中点。则下列五个命题
①点E到平面![]() 的距离为
的距离为![]() ;
;
②直线BC与平面![]() 所成的角等于
所成的角等于![]() ;
;
③空间四边形![]() 在正方体六个面内的射影围成的图形中,面积最小的值为
在正方体六个面内的射影围成的图形中,面积最小的值为![]() ;
;
④BE与![]() 所成角为
所成角为![]() ;
;
⑤二面角![]() 的大小为
的大小为![]() ;
;
其中真命题是______。(写出所有真命题的序号)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
(17) (本大题满分12分)已知函数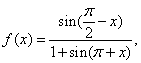
求证:![]() ;
;
已知![]() 的值。
的值。
(18) (本大题满分12分)大学毕业生小张到甲乙丙丁四个单位应聘,各单位是否录用他相互独立。其被录用的概率分别为![]() (允许小张被多个单位同时录用)
(允许小张被多个单位同时录用)
①求小张没有被录用的概率;
②求小张被三个单位录用的概率;
③设录用小张的单位个数为![]() ,求
,求![]() 的分布列和它的数学期望。
的分布列和它的数学期望。
(19) 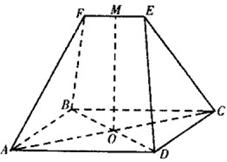 (本大题满分12分)如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,
(本大题满分12分)如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,![]() 为等边三角形,棱
为等边三角形,棱![]() ,M为EF的中点,
,M为EF的中点,
①求证:![]() ;
;
②求二面角E-CD-A的大小;
③求点A到平面CDE的距离。
(20) (本大题满分12分)已知数列![]() 当x=t时,函数
当x=t时,函数![]() 取得极值
取得极值
①求证:数列![]() 是等比数列;
是等比数列;
②记![]() 时,数列
时,数列![]() 中是否存在最大项。若存在,是第几项;若不存在,请说明理由。
中是否存在最大项。若存在,是第几项;若不存在,请说明理由。
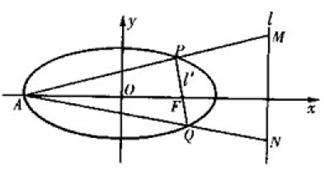
(21) 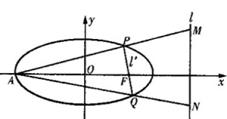 (本大题满分12分)已知椭圆
(本大题满分12分)已知椭圆![]() ,F为其右焦点,A为左顶点,l为右准线,过F的直线
,F为其右焦点,A为左顶点,l为右准线,过F的直线![]() 与椭圆交于异于A的P,Q两点;
与椭圆交于异于A的P,Q两点;
①求![]() 的取值范围;
的取值范围;
②若![]() ;
;
求证:M,N两点的纵坐标之积为定值。
(22) (本大题满分14分)定义在R上的函数
![]() 处取得极值,且
处取得极值,且![]() 的图像在
的图像在![]() 处的切线平行直线y=8x,
处的切线平行直线y=8x,
①求函数![]() 的解析式及极值;
的解析式及极值;
②求不等式![]() 的解集;
的解集;
③对任意![]() ,求证:
,求证:![]()
数学(理科)参考答案及评分说明
一.选择题
1、C 2、B 3、C 4、A 5、D 6、B 7、A 8、C 9、D 10、D 11、A 12、C
二.填空题
13.-3 14.2008 15.4 16.错误!未找到引用源。错误!未找到引用源。错误!未找到引用源。
三.解答题
17.解![]()
错误!未找到引用源。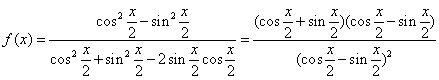
=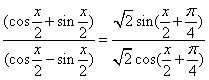
=![]() …………………………………………………………(6分)
…………………………………………………………(6分)
错误!未找到引用源。![]()
=![]()
![]()
 …………………………………………………………(12分)
…………………………………………………………(12分)
18.解:错误!未找到引用源。设未被选中的概率为P![]()
则P![]() =
=![]() ………………………………………………………(6分)
………………………………………………………(6分)
![]() 错误!未找到引用源。设小张被三个单位选中的概率为P
错误!未找到引用源。设小张被三个单位选中的概率为P![]()
则P![]() =
=![]()
=![]() …………………………………………………(12分)
…………………………………………………(12分)
错误!未找到引用源。由题可知,![]() 的可能取值为0,1,2,3,4
的可能取值为0,1,2,3,4
![]() ,
,
![]()
![]()
![]() ,
,
![]() ………………………………………(10分)
………………………………………(10分)
则![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
![]() ……………………………………(12分)
……………………………………(12分)
19.解:错误!未找到引用源。设P,Q分别为AB,CD的中点,连接PQ,EQ,FP,
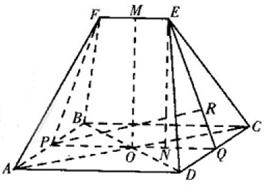 显然:P,O,Q共线;四边形EFPQ为等腰梯形;
显然:P,O,Q共线;四边形EFPQ为等腰梯形;
MO![]() PQ 又
PQ 又![]() DC
DC![]() PQ,DC
PQ,DC![]() EQ
EQ
![]() DC
DC![]() 平面PQEF
平面PQEF
![]() CD
CD![]() MO
MO
则MO![]() 平面ABCD…………………………(6分)
平面ABCD…………………………(6分)
![]() 错误!未找到引用源。由错误!未找到引用源。知:二面角E-CD-A的平面角
错误!未找到引用源。由错误!未找到引用源。知:二面角E-CD-A的平面角![]() EQP,
EQP,
作EN![]() PQ交PQ于N,
PQ交PQ于N,
则N为OQ的中点;![]() …………………………(12分)
…………………………(12分)
错误!未找到引用源。AB//平面CDE,![]() A,P两点到平面CDE的距离相等,
A,P两点到平面CDE的距离相等,
作PR![]() EQ于R,由
EQ于R,由![]()
![]()
![]()
PR=![]() …………………………(12分)
…………………………(12分)
若用坐标法解答,参照评分标准相应给分。
20.解:![]() 时,函数
时,函数![]() 取得极值,
取得极值,
![]() ,即数列
,即数列![]() 是等比数列…………………………(4分)
是等比数列…………………………(4分)
错误!未找到引用源。由错误!未找到引用源。知:![]()
![]()
![]()
![]() ………………………(6分)
………………………(6分)
![]()
![]()
![]()
假设![]() 是数列
是数列![]() 中的最大项,则
中的最大项,则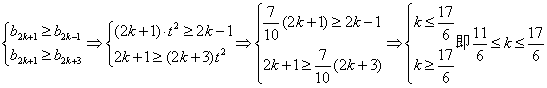
又![]() ………………………(12分)
………………………(12分)
21、解:错误!未找到引用源。i)当直线PQ的斜率不存在时,点 …………………(2分)
…………………(2分)
ii)设直PQ的斜率为k,![]() ,方程为:
,方程为:![]() 代入椭圆方程得:
代入椭圆方程得:![]()
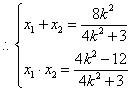
![]()
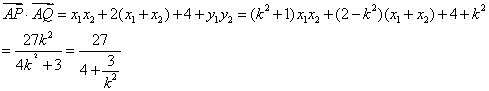
![]()
综上所述: ![]() ………………………(8分)
………………………(8分)
错误!未找到引用源。
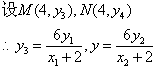
![]() ……………………..(12分)
……………………..(12分)
22、解:错误!未找到引用源。由题设知:![]() ………………..(2分)
………………..(2分)
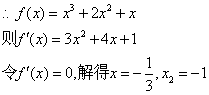
当x变化时,![]() 得变化情况如下表:
得变化情况如下表:
| x |
| -1 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 0 |
|
|
|
![]() …………………….(4分)
…………………….(4分)
错误!未找到引用源。![]()
考虑方程![]() 根得情况:
根得情况:
若k>0,则方程![]() 得根为
得根为![]() 当k>1时,
当k>1时,![]()
![]()
ii)k=1时,不等式得解集为![]()
iii)0<k<1时,不等式的解集为![]()
若k=0,不等式的解集为![]() ………………….(12分)
………………….(12分)
若k<0,不等式的姐姐为![]()
错误!未找到引用源。![]()
由错误!未找到引用源。知:![]() 上的最大值,最小值分别是4,
上的最大值,最小值分别是4,![]()
![]() …………………….(14分)
…………………….(14分)