高三年级数学上学期第二次月考试题
一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的）
1．集合
则
（ ）
A．
B．
C．
D．
2．节假日时，国人发手机短信问候亲友已成为一种时尚，若小李的40名同事中，给其发短信问候的概率为1，0.8，0.5，0.3 的人数分别是8，15，14，3（人），通常情况下，小李应收到同事问候的信息条数为 （ ）
A．27 B．37 C．38 D．28
3、
的
（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．不充分不必要条件
4．设a为正数，
（ ）
A．
B．
C．
D．
5．若函数
的定义域为R，则m的取值范围是 （ ）
A．（0，4） B．[0，4] C．
D．
6．若
、b、c
，则下列不等式成立的是 （ ）
A．
B．
C．
D．
7．在给定的映射
的条件下，点
的原象是（ ）A．
B．
.C.
D.
8．已知数列
为等比数列，且
（ ）
A．
B．
C．
D．
9．已知函数
的图象在点（1，f（1））处的切线方程是
的值是 （ ）
A．
B．1 C．
D．2
|
的反函数的图象大致是 （ ）
11．
（ ）
12．某人于1995年7月1日去银行存款元，存的是一年定期储蓄，1996年7月1日他将到期存款的本息一起取出，在加元之后,续存一年定期存款。此后每年的7月1日他都按照同样的方法在银行取款和存款。设银行一年定期储蓄的年利率r不变,则到2000年7月1日，他将所有存款和利息全部取出，取出的钱数共为 （ ）元。
|
二、填空题（本大题共4个小题，每小题5分，共20分，请把答案填写在题中横线上）
13．不等式
的解集是
14．等差数列中，若
，则
的值为
15．下列函数①
；②
；③
；④
中，满足“存在与x无关的正常数M，使得
对定义域内的一切实数x都成立”的有
（把满足条件的函数序号都填上）
16．观察新生儿的体重，其频率分布直方图如下图所示，则新生儿的体重在
的频率为 。
三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）
17．（本小题满分10分）
18. （本题满分12分）
已知函数
，
（1）若
，求的值
；（2）若
为偶函数，求
。
19．（本题满分12分）
甲、乙两人各进行一次射击，如果两人击中目标概率都是0.8。求
（1）两人都击中目标概率；
（2）其中恰有一人击中目标的概率；
（3）至少有一人击中目标的概率。
20．（本题满分12分）
已知
且
，
，求
的取值范围.
21．（本题满分12分）
若函数
，
（1）求函数的解析式；
（2）若关于x的方程
有三个零点，求实数k的取值范围.
22．（本题满分12分）
已知等比数列中，
，公比
，
又是一个等差数列的第7项、第3项、第1项。
（1）
求等比数列的通项公式
；
（2）
设
，求数列
的前n项和
第二次月考文科数学参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | B | B | B | C | B | B | C | B | A | D |
二、填空题：13. 
14. 
15. 
16. 0.3
三、解答题：
17． 解:
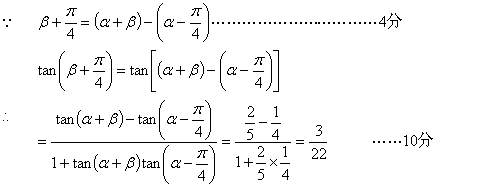
18．解：
（1） 由
，得
，
解之，得 
………………6分
（2）由已知，得
，
又
为偶函数，所以有
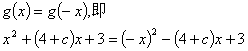
19．解：设“甲射击一次，击中目标”为事件A，“甲射击一次，击中目标” 为事件B,
(1)“两人各射击一次，都击中目标”就是事件
,又由于事件A和B相互独立，
………………4分
（2）“两人各射击一次，其中恰好有一人击中目标”包括“甲击中目标乙击不中目标，即
”或“乙击中目标甲击不中目标，即
”，又这两种情况不可能同时发生，即事件“”与“”是互斥的，所以所求概率为：
………………………………………………………………….............8分
（3）“两人各射击一次，至少有一人击中目标”的概率为：
………………..12分
20、解:由
……………………………………2分
∵ A∩B≠φ,∴B≠φ
设
的解为
,即
∵A∩B≠φ,A∪B={
,∴
……………………………6分
由韦达定理，得
,即
∴a＋b＝6x1－7∈
…………………………………………………………12分
21．解：（Ⅰ）由
，得
…………………………………………………2分
又
， 所以有
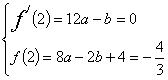………………………………………4分
解之，得
所以函数的解析式为
……………6分
（Ⅱ）由（Ⅰ）得，则
令
22．解：（Ⅰ）设等比数列的公比为
，则有
……………………………………1分
又
是另一等差数列的第7项、第3项、第1项
∴
……………………………………3分
即
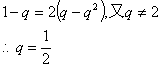
……………6分
（Ⅱ）由（1）得，
