高三年级数学理科月考试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟。
第Ⅰ卷（选择题，共50分）
一．选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.
设集合
，B = {
，则下列结论成立的是
A．
B．
C．
D．
2.
如图，在正六边形ABCDEF中，图中与
模相等且共线的向量(不包含)有
A．1个 B．2个
C．3个 D．4个
3.
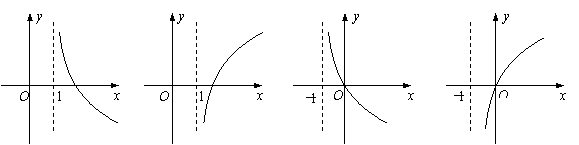如果函数
(a
> 0，a≠1)是增函数，那么函数
的图象大致是
A B C D
4.
若数列
的前8项的值互异，且
对任意的n∈N*都成立，则下列数列中可取遍的前8项值的数列为
A．
B．
C．
D．
5.
已知a、b∈R*，且满足a＋b = 2，则
的最大值是
A．
B．4 C．5 D．
6.
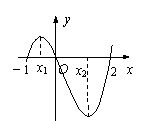如图是函数
的大致图像，则
等于
A．
B．
C．
D．
7.
若对于x∈(1，3)，不等式
≥
恒成立，则实数a的取值范围是
A．
B．
C．
D．
8.
我国股市中对股票的股价实行涨跌停制度，即每天的股价最大的涨幅或跌幅均为10%．某股票连续四个交易日中前两日每天涨停，后两日每天跌停，则该股票现在的股价相对于四天前
A．涨了1.99% B．跌了1.99% C．跌了1% D．没有变化
9.
已知函数
，则方程
的解的个数是
A．1 B．2 C．3 D．4
10.
曲线
在区间
上截直线y = 2与y = －1所得的弦长相等且不为0，则下列对A、a的描述正确的是
A．a = 1，A≥1 B．a = 1，A≤1 C．
，A≤
D．
第Ⅱ卷（非选择题 共100分）
二．填空题：本大题共5小题，每小题5分，共25分。将正确答案填在答题卷上对应题号的横线上。
11. 函数
的最小正周期为 ▲ ．
12. 函数
的定义域是 ▲ ，单调递减区间是 ▲ ．
13.
已知
是方程
的两个根，且
，则
的值是 ▲ ．
14. 歌德巴赫(Goldbach．C．德．1690—1764)曾研究过“所有形如
(
，
为正整数)的分数之和”问题．为了便于表述，引入记号：
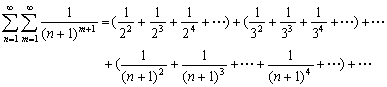
写出你对此问题的研究结论： ▲ (用数学符号表示)．
|
|
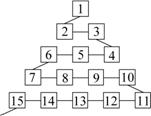
15. 如图是从事网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4(从左至右)出现在第3行；数字7，8，9，10出现在第4行；依此类推．则第99行从左至右算第67个数字为 ▲ ．
三．解答题：本大题共6小题，满分75分。解答应写出文字说明，证明过程或演算步骤。
16.
(本大题满分12分)已知命题p：
≥2，命题q：x2－4x + 4－9m2
≤0 (m＞0)，若
p是q的充分而不必要条件，求实数m的取值范围．
17.
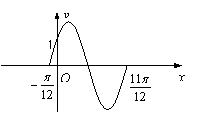(本大题满分12分) 函数
的一段图象过点(0，1)，如图所示
(1)求函数
的解析式；
(2)将函数
的图象按向量a = (
，0)平移，得到函数
，求
的单调递增区间．
18．本大题满分12分)△ABC中，内角A、B、C的对边分别是a、b、c，已知a，b，c成等比数列，且
．
(1)求
的值；
(2)判断等式
有无成立的可能？如果有，求出a、b、c的一组值；如果没有，说明理由)．
19．大题满分12分)某水库年初的存水量为a(a≥10000)，其中污染物的含量为p0，该年每月降入水库的水量与月份x的关系是
(1≤x≤12，x∈N)，且每月流入水库的污水量r，其中污染物的含量为p(p＜r＝，又每月库水的蒸发量也为r(假设水与污染物能充分混合，且污染物不蒸发，该年水库中的水不作它用)．
（1） x个月水库含污比g (x)的表达式(含污比
)；
（2）当p0 = 0时，求水质最差的月份及此月份的含污比．
20．本大题满分13分)已知函数
，t为常数，且t > 0.
(1)若曲线
上一点
处的切线方程为
，求t和y0的值；
(2)若
在区间
上是单调递增函数，求t的取值范围；
(3)当t = 1时，证明：1－
≤ln x≤x－1．
21．(本大题满分14分)已知数列{an}中，
(1)是否存在常数
，使得数列
是等比数列，若存在，求出的值，若不存在，说明理由．
(2)设
，证明：
(n≥2，n∈N)．
参考答案
一．选择题：BCCBD CABCD
二．填空题：11．
12．{x x
< 0或x > 2}，[2，+∞) 13．
14．
15．4884
三．解答题：
16．解：由≥2得：－2 < x≤3，
由x2－4x + 4－9m2 ≤0 (m＞0)得：2－3m≤x≤2+3m (m＞0)
∴p：－2 < x≤3，q：2－3m≤x≤2+3m (m＞0) 4分
则 p：
，q：
由已知 p 
q，得A Ü B 8分
从而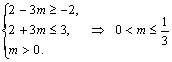 
，故m的取值范围是(0，
]． 12分
17．(1)解：由图知：
，于是
2分
又
，∴
，故
4分
将(0，1)代入
得：A = 2
因此，
6分
(2)解：依题意：
8分
∴
10分
∴函数的单调递增区间为
12分
18．(1)解：∵a，b，c成等比数列 ∴b2 = ac
∴由正弦定理得：
2分
∵，∴
，故
4分
又
， ∴
，即
∴
6分
8分
(2)解：不可能成立．
取AC中点O，连结BO
∵
，若，则BO⊥AC 10分
从而
，即a = c，又b2 = ac， ∴a = b = c，∴
∴
，与已知矛盾，∴不可能成立． 12分
19．(1)解：第x月水库含污染物p0 + px，库容总量 = 
2分
当1≤x≤6 (x∈N)时，
此时库容量 = a + 14 + 15 + … + (13 + x)
= 
4分
当7≤x≤12
(x∈N)时，
此时，库容总量 = a + 99 + 20 + 19
+ … + (27－x) =
6分
∴ 
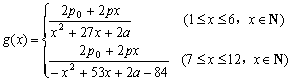8分
(2)解：∵p0 = 0，a≥10000，当1≤x≤6时，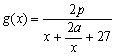
令
，且1≤x1
< x2≤6，则
∴
在[1，6]上是减函数，且恒大于零，
∴
在区间[1，6]上是增函数，当x = 6时，
10分
当7≤x≤12时，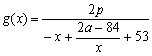
同样可证
在[7，12]上是减函数，且恒大于零.
∴在区间[7，12]上是增函数，当x = 12时，
∵a≥10000，
∴水质量最差的是12月份，其含污比为
12分
20．(1)解：
，∴
由题意得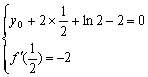
2分
解得：
4分
(2)解：若在区间上是单调递增函数，
则
≥0在
上恒成立，即t≤x恒成立 6分
因为x≥1，∴t≤1，因此0
< t≤1 8分
(3)解：当t = 1时，
，∴
9分
当x
> 1时，
，所以在[1，+∞)单调递增，故f (x)≥f (1)
当0 < x
< 1时，
，所以在(0，1)单调递减，故f (x) > f (1)
又f (1) = 0，所以f (x)≥0，即
≥
① 11分
令
，则
当x
> 1时，
，∴在[1，+∞)单调递减，故g (x)≤g (1)
当0 < x
< 1时，
，所以在(0，1)单调递增，故g (x) < g (1)
而
，所以g (x)≤0，即≤x－1 ②
由①②得：
13分
21．(1)解：若是等比数列，则
即
Þ 
2分
故
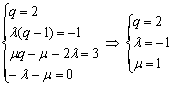4分
∴
故存在
使得数列是等比数列． 6分
(2)证：由(1)知：
是公比为2的等比数列，
∴
，即
故 
8分
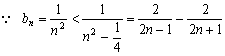
n≥2时，
10分
现证 
(n≥2)
(i)当n = 2时，
，
∴ n = 2时不等式成立 12分
(ii)假设n = k (k≥2)时，
成立
则
∴
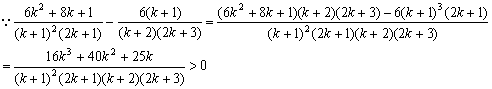
成立
根据(i)(ii)，可知对于n≥2，n∈N都成立． 14分