高三年级文科数学第二次月考试题
总分:150分 考试时间:120分钟
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共12小题,每小题5分,共60分,每小题中给出四个选项,只有一项是符合题目要求的)
1.2sin210°的值是 ( )
A.1 B.-1 C.![]() D.-
D.-![]()
2.不等式![]() 的解集是 ( )
的解集是 ( )
A.(-![]() ,0) B.(0,1)
,0) B.(0,1)
C.(1,+![]() ) D.(-
) D.(-![]() ,0)
,0)![]() (1,+
(1,+![]() )
)
3.等差数列![]() 为 ( )
为 ( )
A.8 B.9 C.10 D.11
4.命题, “若a>b,则![]() ”的逆否命题是 ( )
”的逆否命题是 ( )
A.若a>b,则![]() B.若
B.若![]() ,则a>b
,则a>b
C.若a≤b,则![]() D.若
D.若![]() ,则a≤b
,则a≤b
5.若奇函数![]() ( )
( )
A.0 B.1 C.-![]() D.
D.![]()
6.下列各式中,值为![]() 的是 ( )
的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
7.在等比数列![]() ( )
( )
A.3 B.18 C.9 D.81
|
9.设![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.将函数![]() 平移后所得函数的图象的解析式是 ( )
平移后所得函数的图象的解析式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.函数![]() 的图像为C,以下三个论断中,正确论断的个数是 ( )
的图像为C,以下三个论断中,正确论断的个数是 ( )
①图像C关于直线![]() 对称;
对称;
②函数![]() 内是增函数;
内是增函数;
③由![]() 个单位长度可以得到图像C.
个单位长度可以得到图像C.
A.0 B.1 C.2 D.3
12.已知函数![]() 上恒为正,则a的取值范围是 ( )
上恒为正,则a的取值范围是 ( )
A.(-2,2) B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共4个小题,每小题4分,共16分)
13.已知![]() 的终边在第
象限.
的终边在第
象限.
14.已知数列![]() 的前n项和
的前n项和![]() = .
= .
15.已知等比数列的公比![]() =
.
=
.
16.函数![]() 的最小为
.
的最小为
.
三、解答题(本大题共6小题,满分74分,解答应写出文字说明、证明过程或演算步骤)
17.(13分)已知数列![]() 为等差数列,
为等差数列,![]() 为其前n项和,且
为其前n项和,且![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)求使得![]() 成立的n的集合.
成立的n的集合.
18.(13分)已知![]() 为第二象限角,
为第二象限角,![]() 为第三象限角,
为第三象限角,![]()
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
19.(12分)已知函数![]()
(1)求函数![]() 的值域;
的值域;
(2)若函数y=![]() 的图象与直线y=-1的两个相邻交点的距离为
的图象与直线y=-1的两个相邻交点的距离为![]() ,求函数y=
,求函数y=![]() 的单调递增区间.
的单调递增区间.
20.(12分)已知数列![]() 的前n项的和为Sn,且
的前n项的和为Sn,且![]()
求:
(1)数列![]() 的通项公式;
的通项公式;
(2)![]() 的值.
的值.
21.(12分)某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x(单位:元,![]() )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
22.(12分)已知![]() 为锐角,且
为锐角,且![]() 函数
函数![]() 数列
数列![]() 的首项
的首项![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)求证:![]()
(3)求证:![]()
参考答案
一、选择题
1.B 2.D 3.C 4.D 5.D 6.B 7.C 8.D 9.A 10.A
11.C 12.C
二、填空题
13.三 14.2n 15.90 16.-2
三、解答题
17.(1)由题,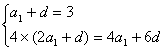 (3分)
(3分)
故![]() (5分
(5分
![]() 即数列为等比数列 (7分)
即数列为等比数列 (7分)
(2)由![]() (9分)
(9分)
![]() (11分)
(11分)
![]() (12分)
(12分)
故n的集合为:{1,2,3,4}(13分)
18.解:(1)因为![]() 是第二象限的角,
是第二象限的角,![]()
![]() (2分)
(2分)
![]() (3分)
(3分)
![]() (6分)
(6分)
(2)因为![]() 为第三象限的角,
为第三象限的角,![]()
![]() (9分)
(9分)
又![]()
![]() (11分)
(11分)
![]() (13分)
(13分)
19.(1)解:![]() (2分)
(2分)
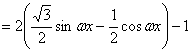
![]() (5分)
(5分)
由![]()
可知函数![]() 的值域为[-3,1].(7分)
的值域为[-3,1].(7分)
(2)解:由题设条件及三角函数图象和性质可知,![]() 的周期为
的周期为![]() ,
,
又由![]() (9分)
(9分)
于是有![]()
解得![]() (11分)
(11分)
所以![]() 的单调增区间为
的单调增区间为![]() (12分)
(12分)
20.(1)由题,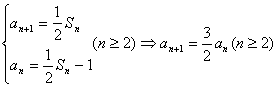 (3分)
(3分)
即![]() 为首项,以
为首项,以![]() 为公比的等比数列(4分)
为公比的等比数列(4分)
又![]() (5分)
(5分)
故![]() (6分)
(6分)
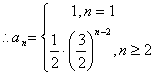 (8分)
(8分)
(2)![]()
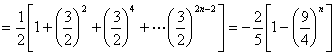 (12分)
(12分)
21.解:(1)设商品降价x元,则多卖的商品数为![]() ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为![]() ,则依题意有
,则依题意有![]() (4分)
(4分)
又由已知条件,![]() ,于是有k=6(5分)
,于是有k=6(5分)
所以![]() (6分)
(6分)
(2)根据(1),我们有![]() (8分)
(8分)
| x |
| 2 | (2,12) | 12 |
|
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
故![]() 达到极大值,因为
达到极大值,因为![]()
所以定价为30-12=18元能使一个星期的商品销售利润最大.(12分)
22.(13分)解:
(1)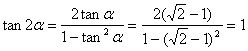
又![]() 是锐角
是锐角 ![]()
![]()
![]() (4分)
(4分)
(2)![]()
![]() 都大于0
都大于0
![]() (6分)
(6分)
(3)![]()
![]()
![]()
![]() (9分)
(9分)
![]()
又![]()
![]()
![]() (12分)
(12分)