高三年级理科数学第二次月考试题（）
总分：150分 考试时间：120分钟
第Ⅰ卷（选择题 共50分）
一、选择题（每小题5分，共50分）
1．已知
等于 （ ）
A．
B．7 C．－ D．－7
2．函数
的图象 （ ）
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．关于
轴对称
3．已知
，则p是q的 （ ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
4．函数
单调增区间为 （ ）
A．
B．
C．
D．
5．设向量
的有向线段首位相接能够成三角形，则向量
为 （ ）
A．（4，6） B．（－4，6） C．（－4，－6） D．（4，－6）
|
A．
B．
C．
D．
7．已知O为△ABC所在平面内一点，满足
，则O为△ABC的 （ ）
A．外心 B．内心 C．垂心 D．重心
8．若互不相等的实数a，b，c成等差数列，c，a，b成等比数列，且
，则a=
（ ）
A．4 B．2 C．－4 D．－2
9．已知实数a，b均不为零，
等于（ ）
|
B．
C．－ D．－
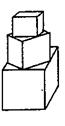
10．有一塔形几何体由若干个正方体构成，构成方式如图所示，
上层正方体下底面的四个顶点是下层正方体上底面各边的
中点.已知 最底层正方体的棱长为2，且该塔形的表面积
（含最底层正方体的底面面积）超过39，则该塔形中正方
|
A．5； B．6；
C．7； D．8；
|
二、填空题（每小题4分，共24分）
11．设
，函数
有最小值，则不等式
的解集为
.
12．若
，则
=
.
13．把函数
的图象向左平移m个单位（m>0），所得图象关于y轴对称，则m的最小值是
.
14．在等差数列
中，
，前n项和为Sn，若Sn取得最大值，则n= .
15．在△ABC中，A，B，C成等差数列，则
=
.
16．①存在
②存在区间（a,b）使
为减函数而
③
在其定义域内为增函数
④
即有最大、最小值，又是偶函数
⑤
最小正周期为
以上命题错误的为 .
三、解答题（17—20每题13分，21—22每题12分，共76分）
17．已知
，若A是B的真子集，求实数m的取值范围.
18．若函数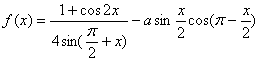
（1）若
，求
的单调增区间.
（2）若的最大值为2，试确定常数a的值.
19．（13分）在△ABC中，∠A、∠B、∠C的对边分别为a，b，c，且满足
（1）求角B的大小.
（2）设
的最大值为5，求k的值.
20．已知x=1是函数
的一个极值点，其中
（1）求m与n的关系表达式；
（2）当
时，函数y=的图象上任意一点的切线斜率恒大于3m，求m的取值范围.
21．设函数的定义域为（0，+
），且对任意的正实数x,y都有
恒成立.已知
.
（1）判断
上的单调性，并说明理由.
（2）一个各项为正数的数列满足
，其中
是数列的前n项的和，求数列的通项
.
22．（12分）设数列的前n项和
（1）求首项a1;
（2）求数列的通项an；
（3）设
参考答案
一、选择题
1．A 2．D 3．B 4．B 5．C 6．D 7．C 8．C 9．B 10．B
|
选A.
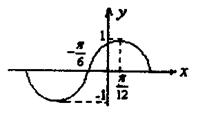
6． D解析：从图象看出，
所以函数的最小正周期为，函数应为
向左平移了
个单位，
即
选D.
8． D解：由互不相等的实数a，b，c成等差数列可设a=b－d，c=b＋d，由 可得b=2，所以a=2－d，c=2+d，又c,a,b成等比数列可得d=6，所以a=－4，选D.
9．B 
10．解：一个正方体时表面记为24，
二个正方体时表面记为24+4×
三个正方体时表面记为24+4×
－d
四个正方体时表面记为24+4×
五个正方体时表面记为
二、填空题
11．
12．
13．
14．8 15． 16．①②③⑤
15．解：
16．①当
时，
故错；
②
为减函数时，
故错；
③错；
④
故对；
⑤无周期.
三、解答题
17．解：集合A：
集合B：
时，m无解，
18．解：（1）
又
的单调增区是为
（2）
由已知有
解之得
19．解：（1）
整理得
（2）
设
，则
∵对称轴
∴当t=1时，
取得最大值.
即
20．解：（1）
（2）
设
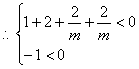
又
21．解：（1）设
为增函数.
（2）由
两式相减得：
22．（1）
再由
整理得
是首项为
，公比为4的等比数列.
即
（2）将
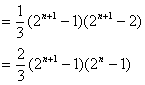
