高三年级理科数学联考试题
一、选择题：本大题共12小题，每小题5分，共60分，将每小题给出的四个选项中的唯一正确的选项填在答题卡相应的题号中。
1．“P或q是假命题”是“非P为真命题”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．已知函数
在区间M上的反函数是其本身，则M可以是 （ ）
A．
B．
C． D．
3．下列函数中,值域为
的函数是 （ ）
A．
B．
C．
D．
4．若不等式
的解集是
，则
的值为 （ ）
A．10 B．—10 C．14 D．—14
5．若关于
的不等式
的解集为空集，则实数
的取值范围为（ ）
A．
B．
C．
D．
6．设
是等差数列
的前项
和，若
，则
等于 （ ）
A．1 B．－1 C．2 D．
7．如果
是平面的三个点，向量
设P为线段AB的垂直平分线CP上任一点，向量
若
，则
等于 （ ）
A．1 B．3 C．5 D．6
8．曲线
在区间
上截直线
与
所得的弦长相等且不为0，则下列描述中正确的是 （ ）
A．
B．
C．
D．
9．若已知
的值，那么以下有四个答案：①
；②
；③
；④
中，正确的是 （ ）
A．①② B．③④ C．①④ D．②③
|
是R上的减函数，
是其图象上的两点，那么不等式
的解集是 （ ）
A．（—1，2） B．
C．
D．
11．设偶函数在R上对任意的
，都有
且当
时，
，则
的值是 （ ）
A．
B．
C．
D．
12．若集合
满足
，则称
为集合的一种分拆，并规定当且仅当
时，与
为集合的同一种分拆，则集合
的不同分拆种数是 （ ）
A．27 B．26 C．9 D．8
二、填空题：本大题共4小题，每小题5分，共20分，将每小题的答案填在答题卡相应的题号中。
13．若
=
.
14．已知△OFQ的面积为S，且
，若
，则向量
的夹角的范围是
.
15．已知等差数列有一性质：若等差数列，则通项为
的数列
也是等差数列。类比上述命题，相应的等比数列有性质：若是等比数列
，则通项为
＝
的数列也是等比数列。
16．下列函数：①
；②
；③
；④
；⑤
。这些函数中最小值为2的函数是 _____ .
三、解答题：本大题共6小题，共70分。解答时应写出必要的文字说明，证明过程或演算步骤。
17．（本小题10分）设方程
的解集为A，方程
的解集为B，已知
，试求实数
的值。
18．（本小题10分）现有命题：若
，且在两个区间
上都是增函数，则在区间
上也是增函数。若认为此命题为真，请给出证明；若认为此命题为假，请对原命题的条件予以补充（不允许变更命题的内容，不允许举例）使原命题成立，先写出补充条件，然后给出证明。
19．（本小题12分）已知函数
为R上的奇函数
，解不等式：
。
20．（本题12分）设函数
，其中
。
（1）若
，且
，求；
（2）若函数
的图象按向量
平移得到函数
的图象，求实数
的值。
21．（本题12分）已知函数
（
在区间上是增函数，
（1）求实数的值组成的集合A；
（2）设关于的方程
的两个非零实根为
，试问：是否存在实数m，使得不等式
对任意
恒成立？若存在，求出m的取值范围，若不存在，请说明理由。
22．（本题14分）已知各项均是正数的数列的前n项和为，
，
，数列满足
（1）求
；
（2）若
，设数列
的前项和
，求证：
；
（3）是否存在自然数M，使得当n
时，
恒成立？若存在，求出相应的M值，
若不存在，说明理由。
参考答案
一、选择题：本大题共12小题，每小题5分，共60分，将每小题给出的四个选项中的唯一正确的选项填在答题卡相应的题号中。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | D | B | A | D | A | D | C | D | A |
|
|
13．
14．
15．
16．___③__
三、解答题：本大题共6小题，共７0分。解答时应写出必要的文字说明，证明过程或演算步骤。
17．（本小题10分）
解：
…………………………………………（3分）
又
,
………………………（6分）
方程有两个相等的实数根
，由韦达定理，有
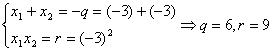
……（10分）
18．（本小题10分）
解：原命题为假， …………………………………………………（3分）
需补充的条件为：
。…………………………………………（5分）
证明：任取
且
若
，由在上是增函数，必有
成立；
若
，由在上是增函数，必有成立；
若
，由题意知
，
又
所以。
综上可知在区间上是增函数。………………（10分）
19．（本小题12分）
解：由于
是R上的奇函数，则
即
……（1分）
且
…………………………………（3分）
由
得
，又由
，（
） ………………………（8分）
即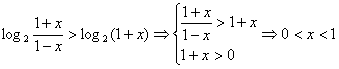
…………………………………（12分）
20．（本题12分）
解：
（1）=
…………………………………………（3分）
又
又
……………………（6分）
（2）将
代入得
是函数的图象按向量平移后的图象的解析式，它与
相同，则
…………（12分）
21．（本题12分）
解：（1）
在[—1，1]上是增函数，
设
，则
解得
……………………………………………………（5分）
（2）由
得
时，是方程
的两实根，则
，
，
……………………（7分）
，因此为使对任意 恒成立，只需
对任意
恒成立， ……………………（9分）
设
，则有
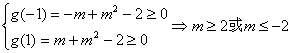，所以存在实数
使对任意恒成立…………………（12分）
22．（本题14分）
解：（1）由
① 
②
①—②得
，又
所以是以
为首项，
为公比的等比数列，
又
……………（5分）
（2）由得
，于是
①
②
①—②得
，
，当
时，
，所以当时，
，又
，所以 。 ……………………（11分）
（3）当
时，要
；当
时，
要
， 所以当时，满足要求的M不存在；
当时，存在M=2，当
时，恒成立。 ……………（14分）