高三数学第一次调研考试
数学试卷·答案·评分标准·讲评设想
A.必做题部分
一、填空题:本大题共14小题,每小题5分,共70分.
1. 已知集合A={1,2,3},集合B={2,3,4},则A∪B= ▲ .
答案:{1,2,3,4}.
2. 已知复数![]() 满足
满足![]() ,则
,则![]() ▲ .
▲ .
答案:![]() .
.
3. 函数![]() 的最小正周期T= ▲ .
的最小正周期T= ▲ .
答案:![]() .
.
4. 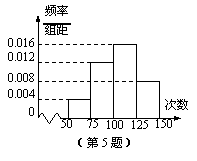 双曲线
双曲线![]() 的渐近线方程为 ▲ .
的渐近线方程为 ▲ .
答案:![]() .
.
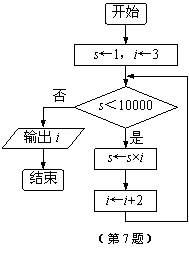
5. 为了了解初中生的身体素质,某地区随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是100,则![]() ▲ .
▲ .
答案:1000.
 6. 袋中有红、黄、绿色球各一个,每次任取一个有放回地抽取三次,球的颜色全相同的概率是 ▲ .
6. 袋中有红、黄、绿色球各一个,每次任取一个有放回地抽取三次,球的颜色全相同的概率是 ▲ .
答案:![]() .
.
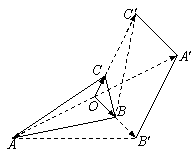
7. 运行如图所示的程序,则输出结果为 ▲ .
答案:13.
8. 数列{an}中,a1=2,a2=1,![]() (n≥2,n∈N),
(n≥2,n∈N),
则其通项公式为an= ▲ .
答案:![]() .
.
9. 在△ABC中,若![]() ,则
,则![]() ▲ .
▲ .
答案:![]() .
.
10.已知PA,PB,PC两两互相垂直,且△PAB、△PAC、△PBC的面积分别为1.5cm2,2cm2,6cm2,则过P,A,B,C四点的外接球的表面积为 ▲ cm2.(注 ![]() ,其中r为球半径)
,其中r为球半径)
答案:26π.
讲评建议:当三线互相垂直时,联想构造长方体.长方体的对角线即为外接球的直径.
11.若不等式![]() ≥0在[1,2]上恒成立,则a的取值范围为 ▲ .
≥0在[1,2]上恒成立,则a的取值范围为 ▲ .
答案:a≤0.
讲评建议:a≤![]() 在[1,2]上恒成立,a≤(
在[1,2]上恒成立,a≤(![]() )min=(
)min=(![]() )min=0.
)min=0.
12.设椭圆![]() 的两个焦点分别为F1,F2,点P在椭圆上,且
的两个焦点分别为F1,F2,点P在椭圆上,且![]() ,
,![]() ,则该椭圆的离心率等于 ▲ .
,则该椭圆的离心率等于 ▲ .
答案:![]() .
.
讲评建议:设PF1=m,则PF2=2m,2c=![]() ,2a=3m,
,2a=3m,![]() .
.
13.给定![]() (n∈N*),定义乘积
(n∈N*),定义乘积![]() 为整数的k(k∈N*)叫做“理想数”,则区间[1,2008]内的所有理想数的和为 ▲ .
为整数的k(k∈N*)叫做“理想数”,则区间[1,2008]内的所有理想数的和为 ▲ .
答案:2026.
讲评建议:换底公式:![]() .
.![]() 为整数,
为整数,![]() ,m∈N*.k分别可取
,m∈N*.k分别可取![]() ,最大值
,最大值![]() ≤2008,m最大可取10,故和为22+23+…+210-18=2026.
≤2008,m最大可取10,故和为22+23+…+210-18=2026.
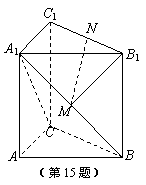
 14.已知点O在△ABC内部,且有
14.已知点O在△ABC内部,且有![]() ,则△OAB与△OBC的面积之比为 ▲ .
,则△OAB与△OBC的面积之比为 ▲ .
答案:4∶1.
讲评建议:如图,作向量![]() ,
,![]() ,
,![]() .则
.则
![]() .
.
 二、解答题:本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤.
二、解答题:本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分12分)
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,
M,N分别为A1B,B1C1的中点.
(1)求证BC∥平面MNB1;
(2)求证平面A1CB⊥平面ACC1A1.
答案:(1)因BC∥B1C1, ………………………………………………………………………2分
且B1C1![]() 平面MNB1, …………………………………………………………………………4分
平面MNB1, …………………………………………………………………………4分
BC![]() 平面MNB1,
平面MNB1,
故BC∥平面MNB1. …………………………………………………………………………6分
(2)因BC⊥AC,且ABC-A1B1C1为直三棱柱, ……………………………………………8分
故BC⊥平面ACC1A1.
因BC![]() 平面A1CB, ……………………………………………………………………………10分
平面A1CB, ……………………………………………………………………………10分
故平面A1CB⊥平面ACC1A1. …………………………………………………………………12分
讲评建议:必修2中的立几初步,必须控制难度,注重答题规范.
16.(本小题满分12分)
已知向量![]() ,
,![]() ,记
,记![]() .
.
(1)求f(x)的解析式并指出它的定义域;
(2)若![]() ,且
,且![]() ,求
,求![]() .
.
答案:(1)∵![]() ,
,
∴![]() …………………………………………2分
…………………………………………2分
![]()
![]()
![]() .……………4分
.……………4分
定义域为![]() . ………………………………………………………………6分
. ………………………………………………………………6分
(2)因![]() ,即
,即![]() >0,
>0,
故![]() 为锐角,于是
为锐角,于是![]() . …………………………………………………9分
. …………………………………………………9分
∴![]() =
=![]()
![]() =
=![]() . ………………………………………………12分
. ………………………………………………12分
讲评建议:第(1)问中,必须注意![]() 中x的条件限制.
中x的条件限制.
第(2)中,学生常会将“![]() ”展开,并结合
”展开,并结合![]() ,求解方程组,求
,求解方程组,求![]() 的值.但三角恒等变换中,“三变”应加强必要的训练.
的值.但三角恒等变换中,“三变”应加强必要的训练.
17.(本小题满分15分)
已知表中的对数值有且只有两个是错误的.
| x | 1.5 | 3 | 5 | 6 | 7 | 8 | 9 | 14 | 27 |
| lgx | 3a-b+c | 2a-b | a+c | 1+a-b-c | 2(a+c) | 3(1-a-c) | 2(2a-b) | 1-a+2b | 3(2a-b) |
(1)假设上表中lg3=2a-b与lg5=a+c都是正确的,试判断lg6=1+a-b-c是否正确?给出判断
过程;
(2)试将两个错误的对数值均指出来并加以改正.(不要求证明)
答案:(1)由lg5=a+c,得lg2=1-a-c.…………………………………………………………3分
∴lg6=lg2+lg3=1-a-c+2a-b=1+a-b-c, ………………………………………………………6分
满足表中数值,也就是lg6在假设下是正确的. ……………………………………………7分
(2)lg1.5是错误的, ……………………………………………………………………………9分
正确值应为3a-b+c-1.……………………………………………………………………………11分
lg7是错误的, ……………………………………………………………………………13分
正确值应为2b+c. ……………………………………………………………………………15分
讲评建议:变题:第(1)小题直接换为:“求证lg3的对数值是正确的”,该怎样证明?(反证法,即先假设lg3=2a-b是错误的,然后推出lg9,lg27均是错误的即可)
注意表中的数据,lg5与lg7至少有一个错误的.
本题旨在考查数据处理、推理与证明的能力,考查对数的运算。问题背景新颖,具有公平性,体现新课标的理念,体现创新性.
18.(本小题满分15分)
设函数![]() .
.
(1)当k=2时,求函数f(x)的增区间;
(2)当k<0时,求函数g(x)=![]() 在区间(0,2]上的最小值.
在区间(0,2]上的最小值.
答案:18.解:(1)k=2,![]() .则
.则![]() =
=![]() .…………………3分
.…………………3分
![]() >0,(此处用“≥”同样给分) ……………………………………………5分
>0,(此处用“≥”同样给分) ……………………………………………5分
注意到x>0,故x>1,于是函数的增区间为![]() .(写为
.(写为![]() 同样给分)
…………7分
同样给分)
…………7分
(2)当k<0时,g(x)=![]() =
=![]() .g(x)=
.g(x)=![]() ≥
≥![]() , ……………9分
, ……………9分
当且仅当x=![]() 时,上述“≥”中取“=”.
时,上述“≥”中取“=”.
①若![]() ∈
∈![]() ,即当k∈
,即当k∈![]() 时,函数g(x)在区间
时,函数g(x)在区间![]() 上的最小值为
上的最小值为![]() ;…11分
;…11分
②若k<-4,则![]() 在
在![]() 上为负恒成立,
上为负恒成立,
故g(x)在区间![]() 上为减函数,
上为减函数,
于是g(x)在区间![]() 上的最小值为g(2)=6-k. ………………………………………………13分
上的最小值为g(2)=6-k. ………………………………………………13分
综上所述,当k∈![]() 时,函数g(x)在区间
时,函数g(x)在区间![]() 上的最小值为
上的最小值为![]() ;
;
当k<-4时,函数g(x)在区间![]() 上的最小值为6-k. ……………………………………15分
上的最小值为6-k. ……………………………………15分
讲评建议:本题涉及对数函数的导数,引导师生重视诸如对数函数、三角函数等导数的运算.
基本不等式的使用必须注意对取“=”条件的验证.
分类讨论,必须要有分有合,也就是最后必须合.
19.(本小题满分18分)
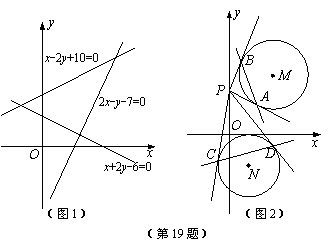 在平面区域
在平面区域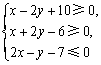 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M.
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M.
(1)试求出⊙M的方程;
(2)设过点P(0,3)作⊙M的两条切线,切点分别记为A,B;又过P作⊙N:x2+y2-4x+![]() y+4=0的两条切线,切点分别记为C,D.试确定
y+4=0的两条切线,切点分别记为C,D.试确定![]() 的值,使AB⊥CD.
的值,使AB⊥CD.
答案:(1)设⊙M的方程为(x-a)2+(y-b)2=r2(r>0),则点(a,b)在所给区域的内部. ……2分
于是有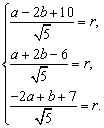 ………………………………………………………………………8分
………………………………………………………………………8分
(未能去掉绝对值,每个给2分)
解得 a=3,b=4,r=![]() ,所求方程为(x-3)2+(y-4)2=5. ……………………………………10分
,所求方程为(x-3)2+(y-4)2=5. ……………………………………10分
(2)当且仅当PM⊥PN时,AB⊥CD. ……………………………………………………14分
因![]() ,故
,故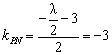 ,解得
,解得![]() =6. ………………………………………………18分
=6. ………………………………………………18分
当![]() =6时,P点在圆N外,故
=6时,P点在圆N外,故![]() =6即为所求的满足条件的解.(本验证,不写,不扣分)
=6即为所求的满足条件的解.(本验证,不写,不扣分)
讲评建议:为了减少计算量,本题中的三直线,两条互相垂直,两条关于水平直线对称.因而也可以通过求角平分线的交点而得出圆心.事实上,一条水平线为y=4,两条互相垂直直线的角平分线所在直线的斜率为![]() ,直线方程为
,直线方程为![]() ,两直线交于点(3,4),即为圆心,后利用圆心到任一条直线的距离即就是圆的半径.
,两直线交于点(3,4),即为圆心,后利用圆心到任一条直线的距离即就是圆的半径.
本题中涉及线性规划,几何概型等考点,但仅是给出它们的背景,不要深入挖掘.
将知识点有机组合而成的综合问题,是命题的一种趋势.
本题中的两处关于评分的说明,须正确的对待.
20.(本小题满分18分)
已知数列![]() 满足
满足![]() ,
,![]() ,n∈N*.
,n∈N*.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)设![]() ,求证
,求证![]() <
<![]() .
.
答案:(1)由已知,得![]() ,∴
,∴![]() 是公比为2的等比数列,首项为
是公比为2的等比数列,首项为![]() .
.
∴![]() ,
,![]() . …………………………………………………………………6分
. …………………………………………………………………6分
(2)![]() .
. ![]() =
=![]() , ①
, ①
2![]() =
= ![]() , ②
, ②
①-②,得 -![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() . …………………………………………………12分
. …………………………………………………12分
(3)当n≥2时,![]()
![]() =
=![]() <
<![]() =
=![]() .
.
∴![]() =
=![]() =
=![]()
=![]() <
<![]() .
…………………………………………………18分
.
…………………………………………………18分
讲评建议:本题问题叙述简捷,形式优美,体现数学的形式美、内在美.
第(1)问,也可采用迭代法来完成,理科生还可使用数学归纳法来实施.
第(2)问,仍作为压轴问题,旨在强调数列中的一些重要方法.
第(3)问,若将结论减弱为![]() <
<![]() .则所提供的解法中,只须保留原来的两项,或者也可以直接将
.则所提供的解法中,只须保留原来的两项,或者也可以直接将![]() ,从第3项起,放大为
,从第3项起,放大为![]() .
.
考生不能放弃压轴题,这也算是命题的一种意图.
B.附加题部分
一、选做题:本大题共4小题,请从这4题中选做2小题,如果多做,则按所做的前两题记分.每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
1. (几何证明选讲)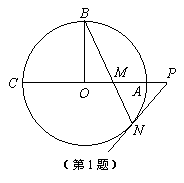 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.
(1)求证:PM2=PA·PC;
(2)若⊙O的半径为![]() ,OA=
,OA=![]() OM,求MN的长.
OM,求MN的长.
答案:(1)连结ON.∵PN切⊙O于N,∴∠ONP=90°.∴∠ONB+∠BNP=90°.
∵OB=ON,∴∠OBN=∠ONB.
∵BO⊥AC于O,∴∠OBN +∠BMO=90°.∴∠BNP=∠BMO=∠PMN,∴PM=PN.
∴PM2=PN2=PA·PC.……………………………………………………………………………6分
(2)OM=2,BO=![]() ,BM=4.
,BM=4.
∵BM·MN=CM·MA=(![]() +2)(
+2)(![]() -2)=8,∴MN=2.………………………………………10分
-2)=8,∴MN=2.………………………………………10分
2. (矩阵与变换)求矩阵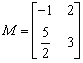 的特征值和特征向量.
的特征值和特征向量.
答案:矩阵M的特征值![]() 满足方程
满足方程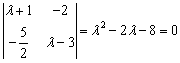 ,
,
解得矩阵![]() 的两个特征值
的两个特征值![]() .…………………………………………………4分
.…………………………………………………4分
将![]() 代人方程
代人方程![]() ,得
,得![]() ,则可取
,则可取![]() 为属于
为属于![]() 的一个特征向量.
的一个特征向量.
将![]() 代人方程
代人方程![]() ,得
,得![]() ,
,
则可取![]() 为属于
为属于![]() 的一个特征向量.………………………………………………9分
的一个特征向量.………………………………………………9分
综上所述: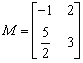 有两个特征值
有两个特征值![]() ,
,
属于![]() 的一个特征向量为
的一个特征向量为![]() ,属于
,属于![]() 的一个特征向量为
的一个特征向量为![]() .……………10分
.……………10分
3. (坐标系与参数方程)已知圆的极坐标方程为![]() ,求它的半径和圆心的极坐标.
,求它的半径和圆心的极坐标.
答案:![]() 可表示为
可表示为![]() ,
,
化为直角坐标方程为![]() ,即
,即![]() ,………………6分
,………………6分
因此该圆的半径为5,圆心的直角坐标为![]() ; ………………………………………8分
; ………………………………………8分
所以圆的半径为5,圆心的极坐标为![]() .…………………………………………………10分
.…………………………………………………10分
4. (不等式选讲)求函数![]() 的最大值.
的最大值.
答案:函数的定义域为![]() ,且y>0.
,且y>0.
![]()
![]() . ………6分
. ………6分
当且仅当![]() 时,取“=”,
……………………………………………8分
时,取“=”,
……………………………………………8分
即![]() 时函数取最大值
时函数取最大值![]() . …………………………………………………………10分
. …………………………………………………………10分
二、必做题:本大题共2小题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
5. 答案:(1)![]() . ……………………………………………………4分
. ……………………………………………………4分
(2)对随机变量X来说,这是一个二项分布,于是
![]() ,k=0,1,2,3.
,k=0,1,2,3.
即P(X=0)=![]() ,P(X=1)=
,P(X=1)=![]() ,P(X=2)=
,P(X=2)=![]() ,P(X=3)=
,P(X=3)=![]() .………………………………8分
.………………………………8分
也就是
| X | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
E(X)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .…………………………………………………10分
.…………………………………………………10分
(或E(X)=np=3×![]() =
=![]() .)
.)
6. 已知点F(0,1),点P在x轴上运动,M点在y轴上,N为动点,且满足![]() ,
,![]() .
.
(1)求动点N的轨迹C方程;
(2)由直线y= -1上一点Q向曲线C引两条切线,切点分别为A,B,求证:AQ⊥BQ.
答案:(1)设N(x,y).
因![]() ,故P的坐标为(
,故P的坐标为(![]() ,0),M(0,-y),于是,
,0),M(0,-y),于是,![]() ,
,![]() .
.
因![]() ,即得曲线C的方程为x2=4y. ………………………………………………5分
,即得曲线C的方程为x2=4y. ………………………………………………5分
(2)设Q(m,-1).由题意,两条切线的斜率k均存在,故可设两切线方程为y=k(x-m)-1.
将上述方程代入x2=4y,得x2-4kx+4km+4=0.
依题意,⊿=(-4k)2-4(4km+4)=0,即k2-mk-1=0.
上述方程的两根即为两切线的斜率,
由根与系数的关系,其积为-1,即它们所在直线互相垂直.…………………………………10分