高三理科数学统一测试试题
数学（理科）试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。
第Ⅰ卷（选择题 共40分）
|
1．设全集U={1，3，5，7，9}，集合A={1，9，a－5}， ={5，7}，则a的值为（ ）
A．2 B．8 C．－2或8 D．2或8
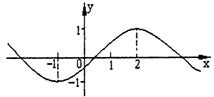
2．若复数
在复平面内对应的点位于 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3．把函数
的图象向右平移
个单位，所得图象对应函数的最小正周期是（ ）
A．
B．2 C．4 D．
4．光线沿直线y=2x+1射到直线y=x上，被直线y=x反射后的光线所在的直线方程为（ ）
A．
B．
C．
D．
5．从4台A型笔记本电脑与5台B型笔记本电脑中任选3台，其中至少要有A型和B型笔
记本电脑各一台，则不同的选取方法共有 （ ）
A．140种 B．84种 C．70种 D．35种
6．对于不重合的两条直线m，n和平面
，下列命题中的真命题是 （ ）
A．如果
，m，n是异面直线，那么
B．如果
，m，n是共面，那么
|
，m，n是异面直线，那么
相交
D．如果
，m，n共面，那么
7．已知数列
的前n项和Sn满足
，那么
的值为（ ）
A．
B．
C．1 D．－2
|
的图象如图所示，则函数
的单调递减区间是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共110分）
二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。
9．若
的展开式中含
项的系数是448，则正实数
的值为
。
|
为参数）的标准方程是
，过这个圆外一点P（2，3）的该圆的切线方程是
。
11．在△ABC中，角A满足条件
，则角A= ，
△ABC的面积为 。
12．若正四面体的四个顶点都在一个球面上，且正四面体的高为4，则该球的半径为 ，体积为 。
13．实数x，y满足不等式组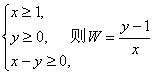
的取值范围是
。
14．已知P是双曲线
的右支上一点，A1，A2分别为双曲线的左、右顶点，F1，F2分别为双曲线的左、右焦点，双曲线的离心率为e，有下列命题：
①双曲线的一条准线被它的两条渐近线所截得的线段长度为
；
②若PF1=ePF2，则e的最大值为
；
③△PF1F2的内切圆的圆心横坐标为a；
④若直线PF1的斜率为k，则
其中正确命题的序号是 。
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤。
15．（本小题满分12分）
已知A、B两点的坐标分别为
（Ⅰ）求
的表达式；
|
（O为坐标原点），求
的值；
（Ⅲ）若
，求函数
的最小值。
16．（本小题满分13分）
有红色和黑色两个盒子，红色盒中有6张卡片，其中一张标有数字0，两张标有数字1，三张标有数字2；黑色盒中有7张卡片，其中4张标有数字0，一张标有数字1，两张标有数字2。现从红色盒中任意取1张卡片（每张卡片被抽出的可能性相等），黑色盒中任意取2张卡片（每张卡片抽出的可能性相等），共取3张卡片。
（Ⅰ）求取出的3张卡片都标有数字0的概率；
（Ⅱ）求取出的3张卡片数字之积是4的概率；
（Ⅲ）记ξ为取出的3张卡片的数字之积，求ξ的概率分布及数学期望Eξ。
17．（本小题满分14分）
|
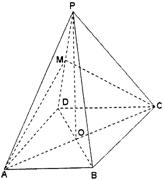
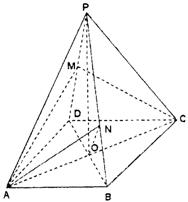
（Ⅰ）证明：PD⊥AC；
（Ⅱ）求二面角A—PB—D的大小；
（Ⅲ）若DM : MP=k，则当k为何值时
直线PD⊥平面ACM？
18．（本小题满分13分）
已知函数
（Ⅰ）当a=－2时，求函数的单调区间和极值；
（Ⅱ）若函数
上是增函数，求实数a的取值范围。
19．（本小题满分14分）
已知点
都在直线l：
上，P1为直线l与x轴的交点，数列成等差数列，公差为1。
|
，
的通项公式；
（Ⅱ）若
问是否存在
，使得
成立？若存在，求出k的值，若不存在，说明理由。
（Ⅲ）求证：
20．（本小题满分14分）
已知抛物线的顶点在原点，对称轴为y轴，且准线方程为
直线l过M（1，0）与抛物线交于A，B两点，点P在y轴的右侧且满足
（O为坐标原点）。
（Ⅰ）求抛物线的方程及动点P的轨迹方程；
（Ⅱ）记动点P的轨迹为C，若曲线C的切线斜率为
，满足
，点A到y轴的距离为a，求a的取值范围。
参考答案
一、选择题：每小题5分，满分40分。
1.D 2.D 3.A 4.B 5.C 6.B 7.C 8.B
二、填空题：每小题5分，满分30分。
（对有两空的小题，第一空3分，第二空2分，第10题每个切线方程各1分）
|
11．
12．3；36 13． 14．①③④
三、解答题：本大题满分80分。
15．（本小题满分12分）
解：（I）
……………………1分
……………………………………………………2分
=
=
…………………………………………3分
（Ⅱ）
………………………………………………4分
又
………………………………6分
………………………………………………………………7分
（Ⅲ）
=
…………………………………………8分
……………………………………………9分
当
时，的最小值为－42，此时
………………10分
当
时，的最小值为4+8，此时
…………………11分
当
时，的最小值为0，此时
……………………12分
16．（本小题满分13分）
解：（I）记“取出的3张卡片都标有数字0”为事件A.…………………………1分
…………………………………………………………2分
（Ⅱ）记“取出的3张卡片数字之积是4”为事件B。
……………………………………5分
（Ⅲ）ξ的可能取值为0，2，4，8 …………6分
………………8分
； …………9分
； …………………………10分
ξ的概率分布列为：
| ξ | 0 | 2 | 4 | 8 | ||
| P |
|
|
|
 |
…………13分
17．（本小题满分14分）
解：（I）∵PO⊥平面ABCD
∴DO为DP在平面ABCD内的射影……………………1分
又AC⊥BD
∴AC⊥PD………………………………………………3分
（Ⅱ）方法1：
过O作ON⊥PB于N，连结AN。
∵PO⊥平面ABCD，
又
平面ABCD，
|
由已知AO⊥BD，BD∩PO=O
∴AO⊥平面PBD。 …………………………5分
∴ON为AN在平面PBD内的射影，
∴PB⊥AN.
∴∠ANO为二面角A—PB—D的平面角。 ……6分
在Rt△AOD中，AO=1。
∵PO⊥平面ABCD，
∴OA为PA在底面ABCD内的射影
∴∠PAO为直线PA与底面ABCD所成的角，
∴∠PAO=60° …………67分
∴Rt△POA中，PO=
∵四边形ABCD为等腰梯形
∴△ABD≌△BAC
∴∠ABD=∠BAC
∴OA=OB=1 …………………………8分
在Rt△POB中，PB=2
∴
在Rt△AON中，
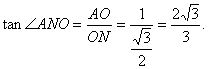………………9分
∴二面角A—PB—D的大小为 
…………10分
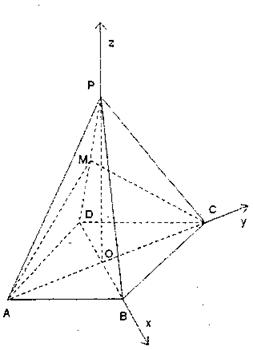
方法2：
如图，以O为坐标原点，OB，OC，OP所在直线分别为x轴，
y轴，z轴建立空间直角坐标系.……………………4分
A（0，－1，0），B（1，0，0）
P（0，0，
O（0，0，0）……………………5分
|
……6分
∵PO⊥平面ABCD
又AO
平面ABCD，
∴PO⊥AO
由已知AO⊥BD，BD∩PO=O
∴AO⊥平面PBD。
∴
为平面PBD的法向量。
∴
…………7分
设
为平面PAB的法向量。
则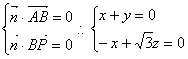
……8分
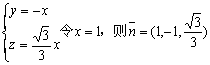……9分
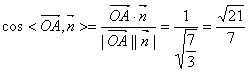
∴二面角A—PB—D的大小为
………………………………10分
（Ⅲ）当DM：MP=1时，直线PD⊥平面ACM…………11分
|
∴OA为PA在底面ABCD内的射影。
∴∠PAO为直线PA与底面ABCD所成的角，
∠PAO=60°
又∵在Rt△AOD中，∠DAO=60°
∴Rt△AOD≌Rt△AOP。
∴AD=AP。
∵PM=MD，
∴PD⊥AM ………………13分
由（Ⅰ）可知PD⊥AC
∵AM∩AC=A
∴直线PD⊥平面ACM …………………………14分
18．（本小题满分13分）
解：（I）函数的定义域为
………………………………………1分
当
时，
………………3分
当x变化时，
的变化情况如下：
| x | （0，1） | 1 | （1，+∞） |
|
| － | 0 | + |
|
| ↘ | 极小值 | ↗ |
………………………………………5分
由上表可知，函数的单调递减区间是（0，1）；
单调递增区间是（1，+∞）。
极小值是 
………………………………6分
（Ⅱ）由
………………7分
又函数
上单调增函数，
则
上恒成立， ……………………8分
即不等式
上恒成立
也即 
上恒成立 ………………10分
又
为减函数， ………………12分
所以
所以 
a的取值范围为
………………………………13分
19．（本小题满分14分）
解（I）由题意知P1（－1，0）…………………………………1分
∴
………………………………………………2分
∴
∴
（Ⅱ）若k为奇数，则
无解…………………………………………………………6分
若k为偶数，则
…………………………………8分
综上，存在k=4使成立.…………………………9分
（Ⅲ）证明：
（1）当
成立。………………11分
（2）当n≥3，n∈N*时，
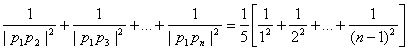
…………………………………………12分
成立.………………………………………………13分
综上，当
成立……………14分
20．（本小题满分14分）
解：（Ⅰ）由题意知抛物线的方程为
∴p=1，抛物线的方程为 
……………………2分
直线l的斜率不存在时，直线l与抛物线交于一点，不符合题意。 …………3分
于是设直线l的方程为 
联立 
设两交点为
则△=4k2－8k>0
……………………4分
∴
……………………5分
设
∵
∴
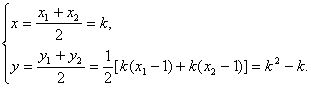
消去k得
……………………7分
又∵P点在y轴的右侧 ∴x>0，
又∵
………………8分
∴动点P的轨迹方程为
（Ⅱ）∵曲线C的方程为
∴切线斜率
………………9分
∴
…………10分
∵
，
又
∴
∴
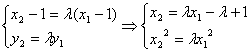
解得
…………12分
∴
………………13分
∴a的取值范围是：
……………………14分