高三第一次联考数学试题
（文科）
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．
第I卷（选择题 共50分）
一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个备选项中，只有一项是符合题目要求的．）
1．集合
，若对于运算“
”：“若
，则
”，则运算“”可以是
（ ）
A．加法 B．减法 C．除法 D．乘法
2．“
或
是假命题”是“非为真命题”的 （ ）
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
3．已知
在区间
上的反函数是其本身，则可以是
（ ）
A．
B．
C．
D．
4．若向量
，则数列
是 （ ）
A．等差数列 B．既是等差又是等比数列
C．等比数列 D．既非等差又非等比数列
5．设
，若
，且
，则
的取值范围是
（ ）
A．
B．
C．
D．
6．数列
中，
，且数列
是等差数列，则
等于
（ ）
A．
B．
YCY C．
D．5
7．已知二面角
的大小为50°，
、
是两条异面直线，则下面的四个条件中，一定能使和所成的角为50°的是
（ ）
A．
B．
C．
D．
8．设圆过双曲线
的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离为
（ ）
A．4 B．
C．
D．5
9．曲线
在区间
上截直线
与
所得的弦长相等且不为0，则下列描述中正确的是
（ ）
A．
B．
C．
D．
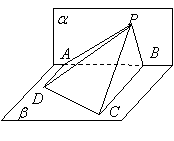
10．如图，
所在的平面
和四边形
所在的平面
垂直，且
， 
， 
，
，
，则点
在平面内的轨迹是 （ ）
A．圆的一部分
B．椭圆的一部分
C．双曲线的一部分
D．抛物线的一部分
第Ⅱ卷（非选择题 共100分）
二、填空题（本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置．）
11．函数
的定义域为
，值域为
，则
=________．
12．如果
，则把变量________的值增加1会使
的值增加最大（填入
中的某个字母）．
13．已知l是曲线
的切线中倾斜角最小的切线，则l的方程是 ．
14．已知底面三角形的边长分别为3、4、5，高为6的直三棱柱形的容器，其内放置一气球，使气球充气且尽可能地膨胀（保持为球的形状），则气球表面积的最大值为
（用含有
的式子表示）.
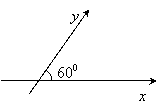15．如图，在平面斜坐标系
中，
，平面上任一点在斜坐标系中的斜坐标是这样定义的：若
=xe1+ye2（其中e1、e2分别为与x轴、y轴方向相同的单位向量），则P点的斜坐标为（x，y）. 若P点的斜坐标为（3，－4），
则点P到原点O的距离PO=________．
三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤．）
16．（本小题满分12分）
、、
为
的三内角，且其对边分别为a、b、c，若
，
，且
．
（1）求角；
（2）若
，三角形面积
，求
的值．
17．（本小题满分12分）
箱中装有15张大小、重量都一样的卡片，每张卡片正面分别标有1到15中的一个号码，正面号码为
的卡片反面标的数字是
．（卡片正反面用颜色区分）
（1）如果任意取出一张卡片，试求正面数字大于反面数字的概率．
（2）如果同时取出两张卡片，试求他们反面数字相同的概率．
18．（本小题满分12分）
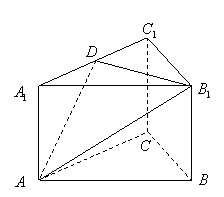
如图，正三棱柱
的底面边长为
，侧棱长为
，点
在棱
上．
（1）若
，求证：直线
平面
；
（2）若
，二面角
平面角的大小为
，求
的值.
19．（本小题满分12分）
设
,其导函数
的图像经过点
,且f(x)在
时取得极小值－8，
（1）求
的解析式；
（2）若对
都有
恒成立，求实数m的取值范围．
20．（本小题满分13分）
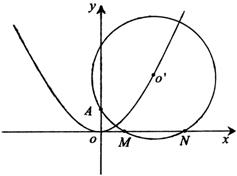
已知⊙
过定点A(0,p)(p>0)，圆心在抛物线C：x2=2py上运动，MN为圆在x轴上所截得的弦.
(1)当点运动时，
是否有变化？并证明你的结论；
(2)当
是
与
的等差中项且M，N在原点O的右侧时，试判断抛物线C的准线与圆是相交、相切还是相离，并说明理由.
21．（本小题满分14分）
对
，不等式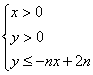
所表示的平面区域为
，把内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成一列点：
（1）求
，
（2）若
（
为非零常数），问是否存在整数，使得对任意，都有
．