高三第一次联考数学试题
(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第I卷(选择题 共50分)
一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.集合![]() ,若对于运算“
,若对于运算“![]() ”:“若
”:“若![]() ,则
,则![]() ”,则运算“
”,则运算“![]() ”可以是
( )
”可以是
( )
A.加法 B.减法 C.除法 D.乘法
2.“![]() 或
或![]() 是假命题”是“非
是假命题”是“非![]() 为真命题”的
( )
为真命题”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知![]() 在区间
在区间![]() 上的反函数是其本身,则
上的反函数是其本身,则![]() 可以是
( )
可以是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若不等式![]() 的解集为
的解集为![]() ,则实数
,则实数![]() 的值为( ).
的值为( ).
A. ![]() B.
B.![]() C.36
D.
C.36
D.![]()
5.曲线![]() 在区间
在区间![]() 上截直线
上截直线![]() 与
与![]() 所得的弦长相等且不为0,则下列描述中正确的是
( )
所得的弦长相等且不为0,则下列描述中正确的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
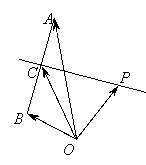 6.如图,
6.如图,![]() 是平面上的三点,向量
是平面上的三点,向量![]() a,
a, ![]() b,设
b,设![]() 为线段
为线段![]() 的垂直平分线
的垂直平分线![]() 上任意一点,向量
上任意一点,向量![]() p.若a=4,b=2,则p(a
p.若a=4,b=2,则p(a ![]() b)等于 ( )
b)等于 ( )
A.1 B.3
C.5 D.6
7.如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L形(每次旋转90°仍为L形图案),那么在由![]() 个小方格组成的方格纸上可以画出不同位置的L形图案
个小方格组成的方格纸上可以画出不同位置的L形图案
 的个数是( )
的个数是( )
A.16
B.32
C.48
D.64
8.设圆过双曲线![]() 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为
( )
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为
( )
A.4
B.![]() C.
C.![]() D.5
D.5
9.设![]() 是
是![]() 的展开式中
的展开式中![]() 的一次项的系数,则
的一次项的系数,则![]() 的值是
( )
的值是
( )
A.16 B.17 C.18 D.19
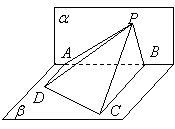 10.如图,
10.如图,![]() 所在的平面
所在的平面![]() 和四边形
和四边形![]() 所在的平面
所在的平面![]() 垂直,且
垂直,且![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,则点
,则点![]() 在平面
在平面![]() 内的轨迹是 ( )
内的轨迹是 ( )
A.圆的一部分
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置.)
11.函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,则
,则![]() =________.
=________.
12.如果![]() ,则把变量________的值增加1会使
,则把变量________的值增加1会使![]() 的值增加最大(填入
的值增加最大(填入![]() 中的某个字母).
中的某个字母).
13.数列![]() 中,
中,![]() ,且数列
,且数列![]() 是等差数列,则
是等差数列,则![]() =___________.
=___________.
14.已知![]() ,记
,记![]()
![]()
![]() ,则
,则![]() ________.
________.
15.如图,设平面![]() ,AB⊥
,AB⊥![]() ,CD⊥
,CD⊥![]() ,垂足分别为B、D.若增加一个条件,就
,垂足分别为B、D.若增加一个条件,就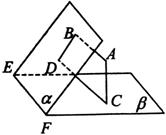 能推出BD⊥EF.故有:
能推出BD⊥EF.故有:
①AC⊥![]() ;
;
②AC与![]() 、
、![]() 所成的角相等;
所成的角相等;
③AC与CD在![]() 内的射影在同一条直线上;
内的射影在同一条直线上;
④AC∥EF.
那么上述几个条件中能成为增加条件的是_______(填上你认为正确的所有答案序号).
三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.)
16.(本小题满分12分)
![]() 内接于以O为圆心,1为半径的圆,且
内接于以O为圆心,1为半径的圆,且![]() .
.
(1)求数量积![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 的面积.
的面积.
17.(本小题满分12分)
箱中装有15张大小、重量一样的卡片,每张卡片正面分别标有1到15中的一个号码,正面号码为![]() 的卡片反面标的数字是
的卡片反面标的数字是![]() (正反面可以用颜色区分)
(正反面可以用颜色区分)
(1)如果任意取出一张卡片,试求正面数字大于反面数字的概率;
(2)如果同时取出两张卡片,试求他们反面数字相同的概率.
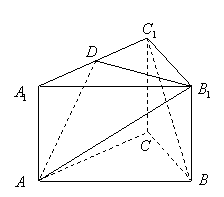
18.(本小题满分12分)
如图,正三棱柱![]() 的底面边长为
的底面边长为![]() ,侧棱长为
,侧棱长为![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(1)若![]() ,求证:直线
,求证:直线![]() 平面
平面![]() ;
;
(2)是否存点![]() , 使平面
, 使平面![]() ⊥平面
⊥平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
 (3)请指出点
(3)请指出点![]() 的位置,使二面角
的位置,使二面角![]() 平面角的大小为
平面角的大小为![]() .
.
19.(本小题满分12分)
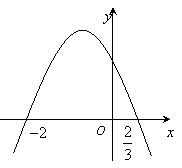 设
设![]() 的极小值为
的极小值为![]() ,其导函数
,其导函数![]() 的图像经过点
的图像经过点![]() ,如图所示,
,如图所示,
(1)求![]() 的解析式;
的解析式;
(2)若对![]() 都有
都有![]() 恒成立,
恒成立,
求实数![]() 的取值范围.
的取值范围.
20.(本小题满分13分)
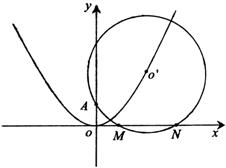
已知⊙![]() 过定点A(0,p)(p>0),圆心
过定点A(0,p)(p>0),圆心![]() 在抛物线x2=2py上运动,MN为圆
在抛物线x2=2py上运动,MN为圆![]() 在x轴上所截得的弦。
在x轴上所截得的弦。
(1)当![]() 点运动时,
点运动时,![]() 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;
(2)当![]() 是
是![]() 与
与![]() 的等差中项时,试判断抛物线C的准线与圆
的等差中项时,试判断抛物线C的准线与圆![]() 的位置关系,并说明理由。
的位置关系,并说明理由。
21.(本小题满分14分)
对![]() ,不等式
,不等式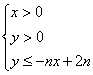 所表示的平面区域为
所表示的平面区域为![]() ,把
,把![]() 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
![]()
(1)求![]() ,
,![]() ;
;
(2)数列![]() 满足
满足![]() ,且
,且![]() 时
时![]() .证明当
.证明当![]() 时,
时,![]() ;
;
(3)在(2)的条件下,试比较![]() 与4的大小关系.
与4的大小关系.