高三第二次调研测试数学试题
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求:
1．本试卷共4页，包含选择题(第1题～第10题，共10题)、填空题(第11题～第16题共6题)、解答题(第17题～第21题，共5题)三部分。本次考试时间为120分钟,考试结束后，请将本试卷和答题卡一并交回。
2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0．5毫米签字笔填写在试卷及答题卡上。
3．作答非选择题必须用书写黑色字迹的0．5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效。作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，请用橡皮擦干净后，再选涂其它答案。．
4．如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚。
一、选择题：本大题共10小题。每小题5分．共50分,在每小题给出的四个选项中恰有一项是符合题目要求的.
1．函数
的定义域是集合M，函数
的定义域是集合P，则
A 
B 
C 
D 
2．在等比数列
中，
，则
A
864 B
3．直线2x-y+3=0关于直线y=x+2对称的直线方程是
A
x-2y+3=0 B x-2y-3=
4．若平面
平面
，
为两两不重合的三条直线，
且
，则
A 
且
∥
B 
或∥ C 且 
D 或
5．
中，若
，则一定是
A 锐角三角形 B 钝角三角形C 直角三角形 D 等腰三角形
6．函数
在区间
上
A 单调递增 B 单调递减 C 先单调递增后单调递减 D先单调递减后单调递增
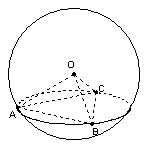7．如图，已知A，B，C是表面积为
的球面上三点，AB=2，BC=4，
，O为球心，则二面角O-AB-C的大小为
A
B 
C 
D
8．一圆形纸片的圆心为O点Q是圆内异于O点的一定点，点A是圆周上一点，把纸片折叠使点A与点Q重合，然后抹平纸片，折痕CD与OA交于P点，当点A运动时点P的轨迹是
A 椭圆 B 双曲线 C 抛物线 D 圆
9．方程
的解共有
A 1个 B 2个 C 3个 D 4个
10．如图，某建筑工地搭建的脚手架局部类似于2×3×4
的长方体框架（由24个棱长为一个单位的正方体框架组合而成），一建筑工人从A点沿脚手架到点B，每步走一个单位，且不连续向上登攀则其行走的路线共有
A 150条 B 525条 C 840条 D 1260条
二、填空题：本大题共6小题，每小题5分,共30分,不需要写出解答过程,请把答案直接填写在答题卡相应位置上．
11．不等式
的解集为 ▲
12．函数
的最小正周期T= ▲
13．过双曲线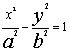
的左焦点且垂直于x轴的直线与双曲线交于M，N，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率= ▲
14．已知O是内一点，
，则
与
的面积之比为
▲
15．在
的二项式展开式中，所有有理项之和为S，当x=2时，S= ▲
16．已知集合A=
，B=
，若
中的元素所对应的点恰好是一个正八边形的顶点，则正数
的值 ▲
三、解答题：本大题共5小题，共70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤．
17．（本小题满分14分）
袋中装有20个不同的小球其中有n（
＞1）个红球，4个蓝球，10个黄球，其余为白球。已知从袋中取出3个颜色相同的彩球（不是白球）的概率为
（1）求袋中的红球、白球各有多少个？
（2）从袋中任取3个小球，求其中一定有红球的概率。
18．（本小题满分14分）
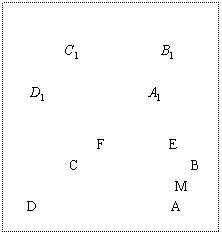如图，在长方体
中，AB=
，BC=1，
=2，M是AB的中点E，F分别为
的中点
（1）求证：直线
平面
（2）求直线AD与平面AEF所成角的大小
 |
19．（本小题满分14分）
将圆
按向量
=（-1，2）平移后得到圆O，直线与院O相交于A，B两点，若圆O上存在点C，使
，求直线的方程及对应的点C的坐标
20．（本小题满分14分）
已知
定义在R上的函数，对于任意的实数a，b都有
，且
（1） 求
的值
（2） 求
的解析式（
）
21．（本小题满分14分）
设函数
（1）求证：为奇函数的充要条件是
（2）设常数
＜
，且对任意x
，＜0恒成立，求实数的取值范围
高三第二次调研测试数学试题
数学参考答案及评分标准
说明：
1、 本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制定相应的评分细则。
2、 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定后续部分的给分，但不得超过该部分正确解答应得分数的一半，如果后续部分的解答有较严重的错误，就不给分。
3、 解答右端所注分数，表示考生正确做到这一步应得的累加分数。
4、 给分或扣分以1分为单位，选择题和填空题不给中间分。
一、选择题：本题考查基本知识和基本运算。每小题5分，满分50分。
1-5 ADADC 6-10 BDACB
二、填空题：本题考查基本知识和基本运算。每小题5分，满分30分。
11．
12. 
13. 2
14. 1:3
15 2048 16 
三、解答题
17.解 (1)设从袋中任取3球全为红球、从袋中任取3球全为蓝球、从袋中任取3球全为黄球；分别为事件A、B、C，由题意知，A、B、C两两互斥，则P（B）=
=
P（C）==
=
4分
故从袋中取出成3个都是相同颜色彩球（不是白球）的概率为
P（A+B+C）= P（A）+P（B）+P（C）=
∴ P（A）=0 6分
由此得从袋中取3球不可能全为红球，从而n≤2，又，n＞1，故n=2
所以：袋中有2个红球4个白球 8分
（2）设袋中任取3个小球，其中一定有红球为事件D，则
P（D）=
=1
=
所以：从袋中任取3个小球，其中一定有红球的概率为
14分
18．解：连结AE并延长交
于点N，则点N为的中点，连结
∵ E，F分别是的中点，
∴ EF∥
2分
在Rt
与Rt
中，∵
∴ Rt∽ Rt ∴
4分
又 
∴
平面
又
EF∥
∴ EF平面
6分
（2） 设
和交于点O，连结AO，过点
作HAO与H 连结
∵ 平面 又
平面AN
∴ 平面AN平面
由 平面AN
平面=AO且HAO
∴H 平面AN
即H 平面AEF
∴ 
在平面AEF上的射影为
则 
为与平面AEF所成的角
10分
在Rt
中，
∴ AO=
∴ 
∴
=
∴ =arcsin
14 分
19．解：圆化为标准方程为
按向量=（-1，2）平移得圆O方程为
2分
由
有
从而
5分
当
时
=（-1，2） ∴C（-1，2）
从而OC的中点为M
又 
∴
直线的方程为
即2x-4y+5=0
9分
同理 
时，C（1，-2）直线的方程为2x-4y-5=0
14分
20．解：（1）令a=b=1 求得
2分
又 
∴
5分
（2） 
∴ 
令 
∴
9分
∴ 数列
是以公差d=
的等差数列 12分
∴ 
∴
∴
14分
21．解：（1）充分性 若 ∴a=b=0
∴
对任意的
都有
∴为奇函数
故充分性成立
2分
必要性 若为奇函数
则对任意的都有恒成立
即 
令x=0 得b=0
令x=a 得a=0
∴ 6分
（2）由＜＜0 当x=0时取任意实数不等式恒成立
当0＜x≤1时
＜0恒成立
也即 
＜＜
恒成立
令
在0＜x≤1上单调递增
∴＞
10分
令
则
在
上单调递减，
单调递增
当＜
时 在0＜x≤1上单调递减
∴ ＜
∴ 
＜ ＜
12分
当≤＜时 ≥
∴ ＜
∴ ＜ ＜
14分