高三级文科数学第一学期期末考试
高三级文科数学试卷
本试卷分选择题和非选择题两部分，满分150分．考试时间120分钟．
注意事项：
1. 答第I卷前，务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上．
2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上．
3. 考试过程不得使用计算器．
一、选择题：本大题共有10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把它选出后在答题卡上规定的位置上用铅笔涂黑．
1．设全集I={-2,-1,-
, 
,,1,2,3}，A={, ,1,2,3}, B={-2,2}，则集合{-2}等于 ( )
A. A∩B B.
I A∩B C. I
A∩ I B D.A∪
I B
2. 已知命题
，
，则( )
A．
,
B．
,
C．,
≤
D．,≤
3. 如图，甲、乙、丙是三个立方体图形的三视图，甲、乙、丙对应的标号正确的是（ ）.
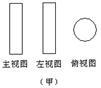
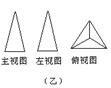
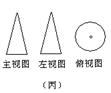
①长方体 ②圆锥 ③三棱锥 ④圆柱
A．④③② B． ②①③ C． ①②③ D． ③②④
4. 已知函数
的最大值是４，最小值是０，最小正周期是
，直线
是其图象的一条对称轴，则下面各式中符合条件的解析式是（ ）
A.
B.
C.
D. 
5. 曲线
在点
处的切线方程为( )
A. 
B.
C. 
D.
6. 直线
平分圆
的周长，则
（
）
A．3 B．5 C．－3 D．－5
7. 与两圆
都外切的圆的圆心的在( )
A. 一个椭圆上 B.双曲线的一支上 C.一条抛物线上 D.一个圆上
8. 已知
=10，
=12，且（3
）·（
）=－36，则与的夹角是（ ）
A.60° B.120° C.135° D.150°
9. 利用计算器，列出自变量和函数值的对应值如下表：
|
| 0.2 | 0.6 | 1.0 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | 3.4 | … |
|
| 1.149 | 1.516 | 2.0 | 2.639 | 3482. | 4.595 | 6.063 | 8.0 | 10.556 | … |
|
| 0.04 | 0.36 | 1.0 | 1.96 | 3.24 | 4.84 | 6.76 | 9.0 | 11.56 | … |
那么方程
的一个根位于下列区间的（ ）.
A.（0.6，1.0） B. （1.4，1.8）
C.（1.8，2.2） D. （2.6，3.0）
10. △ABC内有任意三点不共线的2005个点，加上
三个顶点，共2008个点，把这2008个点连线形成互不重叠（即任意两个三角形之间互不覆盖）的小三角形，则一共可以形成小三角形的个数为（ ）
A．4008 B.4009 C.4010 D.4011
二、填空题：本大题共有5小题，其中第11-13题是必做题，第14-15题是选做题（考生必须从14题或15题中选做一题，若两题都做，只按第14题评分）。每小题5分，满分20分。把各题的答案填在答题卷中规定的位置上，答错位置不给分。
11. A, B两点在平面α的同侧, 且到平面α的距离分别是3cm, 5cm, M是AB的中点，则M到平面α的距离是 cm。
12. 已知函数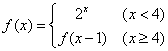
, 则f(2)= ,
_____________.
13. 在约束条件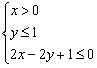
下，目标函数
的最大值为_________.
以下为选做题：
14. 已知抛物线
：
，（
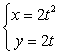为参数）设
为坐标原点，点
在上运动，点
是线段
的中点，则点
的轨迹普通方程为 。
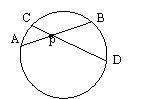15. 如图，圆内的两条弦
、
相交于圆内一点P，已知
，则
三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤
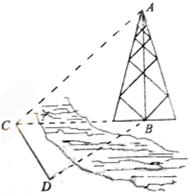16. （本小题满分12分）如图，测量河对岸的塔高
时，可以选与塔底
在同一水平面内的两个测点
与
．测得 
米，
并在点 测得塔顶
的仰角为
, 求塔高AB．
17. （本小题满分12分）已知函数f(x)=4sin2(
+x)-2
cos2x-1(x∈R)
（1）求
的最小正周期、最大值及最小值；
（2）求f(x)的图象的对称轴方程。
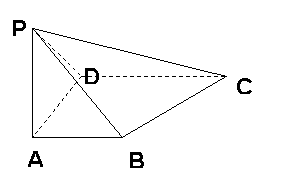
18. （本小题满分14分）如图，四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为直角梯形，
AB∥CD，BA⊥AD，且CD=2AB．若AB=AD=a,直线PB与
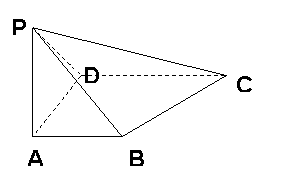CD所成角为450，
(1)求四棱锥P－ABCD的体积VP－ABCD；
(2)求二面角P－CD－B的大小．
19. （本小题满分14分）已知直线
与椭圆
相交于A、B两点.
（1）若椭圆的离心率为
，焦距为2，求线段AB的长；
（2）在（1）的椭圆中，设椭圆的左焦点为F1，求△ABF1的面积。
20. （本小题满分14分）已知二次函数
的图像经过坐标原点，其导函数为
，数列
的前n项和为
，点
均在函数的图像上。
（1）求数列的通项公式；
（2）设
，
是数列
的前n项和，求使得
对所有
都成立的最小正整数m；
21. （本小题满分14分）设f(x)是定义在
的奇函数，g(x)的图象与f(x)的图象关于直线x=1对称，而当
时，
．
（1）求f(x)的解析式；
（2）对于任意的
求证：
（3）对于任意的
求证：
高三级数学科（文科）答题卷
得分栏：
| 题号 | 一 | 二 | 三 | 二卷 总分 | 全卷总分 | |||||
| 16 | 17 | 18 | 19 | 20 | 21 | |||||
| 得分 | ||||||||||
二、填空题：（每小题5分，其中第14题、第15题只选做1题，若两题都做则以14题评定成绩）
11. 12. ， 13.
选做题: 14 15.
三、解答题（要注意在规定区域内用黑色笔作答）
16. （本小题满分12分）
|
17. （本小题满分12分）
18. （本小题满分14分）
19. （本小题满分14分）
20．（本小题满分14分）
21. （本小题满分14分）