高三级理科数学第一学期期末考试
高三级理科数学试卷
本试卷分选择题和非选择题两部分，满分150分．考试时间120分钟．
注意事项：
1. 答第I卷前，务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上．
2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上．
3. 考试过程不得使用计算器．
第一部分（选择题，共50分）
一、选择题：本大题共有8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把它选出后在答题卡上规定的位置上用铅笔涂黑．
1．设全集I={-2,-1,-
, 
,,1,2,3}，A={, ,1,2,3}, B={-2,2}，则集合{-2}等于 ( )
A. A∩B B. I A∩B C. I
A∩ I B D.A∪ I B
2 原命题：“设
＞bc
”以及它的逆命题，否命题、逆否命题中，真命题共有（ ）个.
A、0 B、1 C、2 D、4
3. 如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为（ ）.
A. 1 B. 
C. 
D. 
4. 已知函数
的最大值是４，最小值是０，最小正周期是
，直线
是其图象的一条对称轴，则下面各式中符合条件的解析式是（ ）
A.
B. 
C.
D. 
5. 直线
平分圆
的周长，则
（
）
A．3 B．5 C．－3 D．－5
6. 已知
=10，
=12，且（3
）·（
）=－36，则与的夹角是（ ）
A. 150° B. 135° C. 120° D. 60°
7. 已知a, b∈R, m=
, n=
b2-b+
，则下列结论正确的是（ ）。
A . m≤n B. m≥n C. m>n D.m<n
8.
△ABC内有任意三点不共线的2005个点，加上
三个顶点，共2008个点，把这2008个点连线形成互不重叠（即任意两个三角形之间互不覆盖）的小三角形，则一共可以形成小三角形的个数为（ ）
A．4008 B.4009 C.4010 D.4011
二、填空题：本大题共有7小题，其中第9-12题是必做题，第13-15题是选做题（考生必须从13-15题中选做其中两题，若三题都做，只按前两题评分）。每小题5分，满分30分。把各题的答案填在答题卷中规定的位置上，答错位置不给分。
9. 已知函数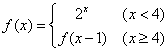
,
则f(-2)=
,
_____________.
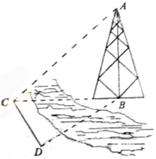
10. 如图，测量河对岸的塔高
时，可以选与塔底
在
同一水平面内的两个测点
与
．测得 
米，并在点 测得塔顶
的仰角为
, 则BC= 米, 塔高AB=
米。
11. 经过抛物线y2=4x的焦点F作与轴垂直的直线, 交抛物线于A、B两点, O是抛物线的顶点,再将直角坐标平面沿
轴折成直二面角, 此时A、B两点之间的距离=
,
∠AOB的余弦值是 ．
12. 已知等比数列{
}的各项均为不等于1的正数，数列
满足
，则数列前n项和的最大值为______________.
以下为选做题：
13. 已知抛物线
：
，（
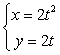为参数）设
为坐标原点，点
在上运动，点
是线段
的中点，则点
的轨迹普通方程为 。
14. 若不等式
无实数解, 则a的取值范围是 .
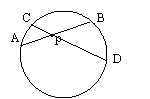15. 如图，圆内的两条弦
、
相交于圆内一点P，已知
，则
三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤
16. （本小题满分12分）已知函数f(x)=4sin2(
+x)-2
cos2x-1（
）
（1）求
的最大值及最小值；
（2）若不等式f(x)－m<2恒成立， 求实数m的取值范围
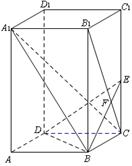17. （本小题满分14分）如图，已知正四棱柱ABCD—A1B1C1D1中，底面边长AB＝2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F，
（1）求证：A1C⊥平面BDE；
（2）求A1B与平面BDE所成角的正弦值。
（3）设P是CC1上的动点(不包括端点C)，求证：△DBP是锐角三角形。
18. （本小题满分14分）通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所用的时间。讲座开始时，学生兴趣激增；中间有一段不太长的时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散。分析结果和实验表明，用f(x)表示学生掌握和接受概念的能力，x表示提出概念和讲授概念的时间（单位：分钟），可有以下的关系式：
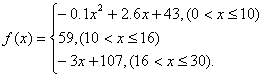
（1） 开讲后多少分钟，学生的接受能力最强？能维持多少时间？
（2） 一个数学难题，需要55(或以上)的接受能力，上课开始30分钟内, 求能达到该接受能力要求的时间共有多少分钟?
（3） 如果每隔5分钟测量一次学生的接受能力，再计算平均值M=
， 它能高于45吗？
19. （本小题满分12分）已知二次函数
的图像经过坐标原点，其导函数为
，数列
的前n项和为
，点
均在函数的图像上。
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，
是数列
的前n项和，求使得
对所有
都成立的最小正整数m；
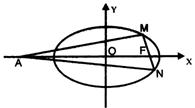
20. （本小题满分14分）已知椭圆
的离心率为
，F为椭圆在x轴正半轴上的焦点，M、N两点在椭圆C上，且
，定点A（－4，0）.
（1）求证：当
时，
；
（2）若当时有
，求椭圆C的方程；
（3）在（2）的条件下，当M、N两点在椭圆C运动时，当
的值为6时, 求出直线MN的方程.
21. （本小题满分14分）已知函数f(x)=
（1） 若h(x)=f(x)-g(x)存在单调增区间，求a的取值范围；
（2）
是否存在实数a>0，使得方程
在区间
内有且只有两个不相等的实数根？若存在，求出a的取值范围？若不存在，请说明理由。
高三级数学科（理科）答题卷
得分栏：
| 题号 | 一 | 二 | 三 | 二卷 总分 | 全卷总分 | |||||
| 16 | 17 | 18 | 19 | 20 | 21 | |||||
| 得分 | ||||||||||
二、填空题：（每小题5分，其中第13题至第15题只选做2题，若3题都做则以前2题评定成绩）
9. ， 10. ， 11. ，
12. 选做题: 13.
14 15.
三、解答题（要注意在规定区域内用黑色笔作答）
16. （本小题满分12分）
17.
（本小题满分14分）
18. （本小题满分14分）
19. （本小题满分12分）
20. （本小题满分14分）
21. （本小题满分14分）