高三联合考试数学卷
数学 试 题
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1．本试卷分第Ⅰ卷（必做题）和第Ⅱ卷（附加题）两部分．第Ⅰ卷共160分，考试时间为120
分钟；第Ⅱ卷共40分，考试时间30分钟．选考历史科的考生只做第Ⅰ卷，选考物理科考生
需做第Ⅰ卷和第Ⅱ卷．
2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷
及答题卡上．考试结束后，请将本试卷和答题卡一并交回．
3．请认真核对监考员所粘贴的条形码上的姓名、考试证号是否与您本人的相符．
4．作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其他位置作答
一律无效．如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚．
第Ⅰ卷（必做题 共160分）
|
|
1．已知集合A=｛x lgx=0｝，B=｛x ＜2x+1＜4｝,则A∩B= ▲ ．
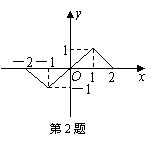
2．函数y = f (x)（ x∈[－2，2]）的图象如图所示，
则f (x)＋f (-x)= ▲ ．
3．在△ABC中，
，则∠B= ▲ ．
4．若z1=a＋2i，z2=3－4i，且
为纯虚数，则实数a的值是 ▲ ．
5．已知a=（2,1）,b =（x,2）,且a＋b与a－2b平行，则x等于 ▲ ．
6．给出数表
请在其中找出4个不同的数，使它们能构成等比数列，这4个数从小到大依次是 ▲ ．
7．设ω是正实数，如果函数f(x)=2sinωx在[－，]上是增函数，那么ω的取值范围是 ▲ ．
8．从观测所得的到数据中取出m个a，n个b，p个c组成一个样本，那么这个样本的平均数是 ▲ ．
9．若长方体相邻三个侧面的面积分别是
，
，
，则该长方体的体积是 ▲ ．
南通四县市高三联合考试数学试题第Ⅰ卷·第1页 （共3页）
10．设直线2x＋3y＋1=0和圆x2＋y2－2x－3=0相交于A，B两点，则弦AB的垂直平分线方程是 ▲ ．
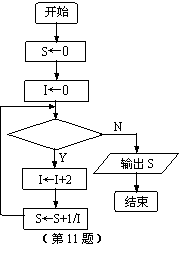11．右图给出的是计算
值的一个程序
框图，其中判断框中应该填的条件是 ▲ ．
12．某厂家根据以往的经验得到下面有关生产销售的统计：
每生产产品x（百台），其总成本为G（x）万元，
G（x）=2＋x；销售收入R(x)（万元）
满足：
要使工厂有赢利，产量x的取值范围是 ▲ ．
13．若a,b均为正实数，且
恒成立，则m的最小值是 ▲ ．
14．下列四种说法：
①命题“
x∈R，使得x2＋1＞3x”的否定是“
x∈R，都有x2＋1≤3x”；
②“m=－2”是“直线(m＋2)x＋my＋1=0与直线（m－2）x＋(m＋2)y－3=0相互垂直”的必要不充分条件；
③在区间[－2，2]上任意取两个实数a，b，则关系x的二次方程x2＋2ax－b2＋1=0的两根都为实数的概率为
；
④过点（
，1）且与函数y=
图象相切的直线方程是4x＋y－3=0．
其中所有正确说法的序号是 ▲ ．
二、解答题：本大题共6小题，共90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
15．（本小题满分14分）
已知向量=（1＋tanx，1－tanx），=（sin(x－)，sin(x＋)）．
（1）求证：⊥；
（2）若x∈[－，]，求的取值范围．
16．（本小题满分14分）
先后2次抛掷一枚骰子，将得到的点数分别记为a,b．
（1）求直线ax＋by＋5=0与圆x2＋y2=1相切的概率；
（2）将a,b,5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．
南通四县市高三联合考试数学试题第Ⅰ卷·第2页 （共3页）
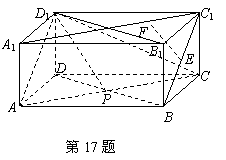
17．（本小题满分15分）
如图，在长方体ABCD—A1B1C1D1中，AB= AD=2．
（1）证明：面BDD1 B1⊥面ACD1；
（2）若E是BC1的中点，P是AC的中点，F是A1C1上的点， C1F=mFA1，试求m的值，使得EF∥D1P．
18．（本小题满分15分）
已知函数f(x)=x2－x＋alnx
(1)当
时，
恒成立，求
的取值范围；
(2)讨论
在定义域上的单调性；
19．（本小题满分16分）
已知F1（－c,0）, F2（c,0） (c＞0)是椭圆的两个焦点，O为坐标原点，圆M的方程是
．
（1）若P是圆M上的任意一点，求证：
是定值；
（2）若椭圆经过圆上一点Q，且cos∠F1QF2=
，求椭圆的离心率；
（3）在（2）的条件下，若OQ=
，求椭圆的方程．
20．（本小题满分16分）
一个数列中的数均为奇数时，称之为“奇数数列”． 我们给定以下法则来构造一个奇数数列｛an｝，对于任意正整数n，当n为奇数时，an=n；当n为偶数时，an=
．
（1）试写出该数列的前6 项；
（2）研究发现，该数列中的每一个奇数都会重复出现，那么第10个5是该数列的第几项？
（3）求该数列的前2n项的和Tn．
南通四县市高三联合考试数学试题第Ⅰ卷·第3页 （共3页）
第Ⅱ卷（附加题 共40分）
一．选做题：本大题共4小题，请从这4题中选做2小题，如果多做，则按所做的前两题记分．每小题10分，共20分．解答时应写出文字说明、证明过程或演算步骤．
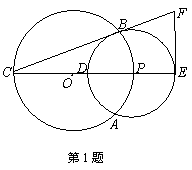1．(几何证明选讲)已知：如图，⊙O与⊙P相交于A，B两点，点P在⊙O上，⊙O的弦BC切⊙P于点B，CP及其延长线交⊙P于D，E两点，过点E作EF⊥CE交CB延长线于点F．若CD=2，CB=2，求EF的长．
2．（矩阵与变换）已知二阶矩阵A的属于特征值－1的一个特征向量为
，属于特征值3的一个特征向量为
，求矩阵A．
3．（坐标系与参数方程）已知曲线C的极坐标方程是
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：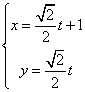
，求直线l与曲线C相交所成的弦的弦长．
4．（不等式选讲）求函数f(x)=sin3xcosx的最大值．
二．必做题：本大题共2道解答题，每题10分，共20分，
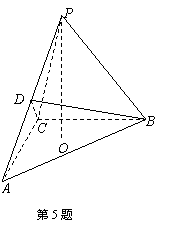
5．在正三棱锥P—ABC中，底面正△ABC的中心为O，D是PA的中点，
PO=AB=2，求PB与平面BDC所成角的正弦值．
6．在一次运动会上，某单位派出了有6名主力队员和5名替补队员组成的
代表队参加比赛．
（1）如果随机抽派5名队员上场比赛，将主力队员参加比赛的人数记为X，求随机变量X的数学期望；
（2）若主力队员中有2名队员在练习比赛中受轻伤，不宜同时上场；替补队员中有2名队员身材相对矮小，也不宜同时上场；那么为了场上参加比赛的5名队员中至少有3名主力队员，教练员有多少种组队方案？
南通四县市高三联合考试数学试题第Ⅱ卷·第1页 （共1页）