高三数学第三次调研测试
数学试卷5、5
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分．考试用时120分钟．
注意事项：
答题前，考生务必将学校、姓名、班级、学号写在答卷纸的密封线内．选择题答案按要求填涂在答卷纸上；非选择题的答案写在答卷纸上对应题目的答案空格内，答案不写在试卷上．考试结束，将答卷纸收回．
参考公式：
如果事件A、B互斥，那么P(A＋B)＝P(A)＋P(B)
如果事件A、B相互独立，那么P(A·B)＝P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率Pn(k)＝CPk(1－P)n
k．
第Ⅰ卷(选择题 共50分)
一.选择题: 本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题意要求的．
1、原命题：“设
”以及它的逆命题，否命题、逆否命题中，真命题共有（ ）个.
A、0 B、1 C、2 D、4
2、坐标平面内向量
与
轴正向上的单位向量
，满足
，则有 （
）
A.
B.
C. 或 D.
3、若函数f(x)=sinax+cosax(a>0)的最小正周期为1，则它的图像的一个对称中心为 （ ）
| |
，0） B．（0，0） C．（－
，0） D．（，0）
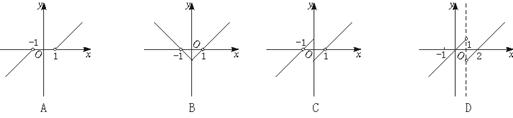
4、奇函数y=f（x）（x≠0），当x∈（0，+∞）时，f（x）=x+1，则函数f（1－）的图象为
（ ）
5、山坡与水平面成30 度角，坡面上有一条与山底坡脚的水平线成30 度角的直线小路，某人沿小路上坡走了一段路后升高了
A．
米
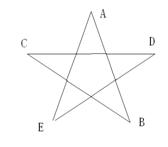
6、如图，五角星魅力无穷，一动点由
处按
顺序依次进行跳跃运动。如果动点由处运动到
处时，记作“1次跳跃”，那么按此规律运动，动点进行了2008次跳跃后，该动点应在 （ ）
A．处 B．
处 C．
处 D．
处
7、已知曲线
及点
,则过点
向曲线
可引切线的条数为 （ )
A 、0 B、
8、设
，给出下列结论：
①
②
③
④
其中正确结论的个数是 （ ）
A．1个 B．2个 C．3个 D．4个
9、在棱长为2R的无盖立方体容器内装满水，先将半径为R的球放入水中，然后再放入一个球，并沉入容器底部，要使溢出的水量最大，则此球的半径是 （ ）
A、
R
B、
R
C、
R
D、
R
10、若
是一个给定的正整数，如果两个整数
用除所得的余数相同，则称
与
对模同余，记作
，例如：
.若:
,则
可以为 （ ）
第Ⅱ卷
二.填空题: 本大题共6小题，每小题5分，共30分.
11、集合
，则的非空真子集的个数为
12、若
则
的取值范围是
、
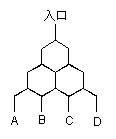
13、图为类似课本研究性学习课题《杨辉三角》中的
竖直平面内一些通道，图中线条都表示通道，一钢珠
从入口处自上而下沿通道自由
|
的概率是 。
14、某商品计划提价，现有四种方案：
方案Ⅰ：先提价m%，再提价n%； 方案Ⅱ：先提价n%，再提价m%；
方案Ⅲ：分两次提价，每次提价（
）%；方案Ⅳ：一次性提价（m+n）%
提价最多的是方案________．
15、按下列程序框图来计算：
如果x=5,应该运算 次才停止。
16、已知
的边长
满足
则
的取值范围为
三.解答题:本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤.
17.(本小题满分12分)
已知向量
=(1，1)，向量
与向量的夹角为
,且
=－1.
（Ⅰ）求向量；
（Ⅱ）设向量
=(1，0)，向量
=(cosx,2cos2(
)),若
=0,记函数
.求此函数的单调递增区间和对称轴方程
18.(本小题满分14分)
正四面体A-BCD的棱长为1，
（Ⅰ）如图(1)M为CD中点，求异面直线AM与BC所成的角；
（Ⅱ）将正四面体沿AB、BD、DC、BC剪开，作为正四棱锥的侧面如图(2)，求二面角M-AB-E的大小；
（Ⅲ）若将图(1)与图(2)面ACD重合，问该几何体是几面体
（不需要证明），并求这几何体的体积。
 |
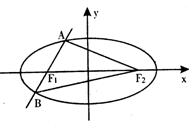19.(本小题满分14分) 已知椭圆
的左、右两个焦点分别为Ｆ１、Ｆ２，过Ｆ１作一直线交椭圆Ｃ于Ａ、Ｂ两点
（Ⅰ）求
面积的最大值。
（Ⅱ）求面积取得最大值时
的值。
20．（本小题满分14分）
已知数列
满足
（Ⅰ）求数列的通项公式；
（Ⅱ）若数列
满足
，证明：是等差数列；
（Ⅲ）证明：
21. (本小题满分16分)
已知函数
（I）当
时，若函数
在区间
上是增函数，求实数
的取值范围；
（II）当
时，
（1）求证：对任意的
，
的充要条件是
；
（2）若关于
的实系数方程
有两个实根
，求证：
且
的充要条件是
数学参考答案
一.选择题: 本大题共10小题，每小题5分，共50分．
1、C 2、D 3、C 4、D 5、B
6、C 7、D 8、B 9、C 10、B
二.填空题: 本大题共6小题，每小题5分，共30分.
11、 6 ;
12、 
；
13、 
；
14、 III；
15、 4 ；
16、 
.
三.解答题:本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤.
17.(本小题满分12分)
解：（1）令n=(x，y)，则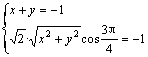
………………………………3分
即
，故n=(-1,0)或n=(0，-1) ……………………6分
（2）∵a=(1，0) n·a=0 ∴n=(0,-1) n+b=
…………………………………………8分
故单调递增区间为
，对称轴为
…………12分
18.(本小题满分14分)
解:（1）取BD中点N.连AN、MN.
就是异面直线AM与BC所成的角…………2分
在
中，
…………4分
（2）取BE中点P.连AP、PM,作
于
过
作
于
连MH.
……………………6分
即
AB 
的平面角…………8分
在
AMP中，
在ABP中，
二面角
的大小为
…………10分
（Ⅲ）若将图(1)与图(2)面ACD重合，
该几何体是5面体…………………12分
这斜三棱柱的体积=3VA-BCD
=3´
´
´
=
…………………14分
19.(本小题满分14分)
∴
20. (本小题满分14分)
解：（1）
，
……………………2分
故数列
是首项为2，公比为2的等比数列。……………………3分
，
…………………………………………4分
（2）
，
……………5分
①
②
②—①得
，即
③……………………8分
④
④—③得
，即
……………………9分
所以数列
是等差数列
（3）
………………………………11分
设
，则
…………13分
………………………………14分
21. (本小题满分16分
（1）当
时，
，
………………1分
在（—1，1）上为单调递增函数，
在（—1，1）上恒成立…………2分
在（—1，1）上恒成立……………………3分
………………………………………………………4分
（2）设
，则
