高三数学第二学期期初联考试题
(考试时间:120分钟+30分钟 总分160分+40分)
命题人:朱占奎( 江苏省靖江中学) 戴年宝( 江苏省姜堰中学) 龚留俊( 江苏省泰兴中学)
审题人:蔡德华(泰兴市第二高级中学) 石志群(泰州市教研室)
注意事项:所有试题的答案均填写在答题纸上,答案写在试卷上的无效.
参考公式:
![]() 次独立重复试验恰有
次独立重复试验恰有![]() 次发生的概率为:
次发生的概率为:![]()
样本数据![]() ,
,![]() ,
,![]() ,
,![]() 的方差
的方差![]()
(![]() 为样本平均数)
为样本平均数)
锥体体积公式![]() 柱体体积公式
柱体体积公式![]() (其中
(其中![]() 为底面面积、
为底面面积、![]() 为高) 用最小二乘法求线性回归方程系数公式
为高) 用最小二乘法求线性回归方程系数公式 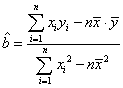 ,
,![]()
A.必做题部分
一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)
1.已知集合![]() ≤
≤![]() ,
,![]() ,则集合A中所有元素之和为 ▲ .
,则集合A中所有元素之和为 ▲ .
2.如果实数![]() 和非零向量
和非零向量![]() 与
与![]() 满足
满足![]() ,则向量
,则向量![]() 和
和![]() ▲ .
▲ .
(填“共线”或“不共线”).
3.△![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() ▲
.
▲
.
4.设![]() ,
,![]() 为常数.若存在
为常数.若存在![]() ,使得
,使得![]() ,则实数a的
,则实数a的
取值范围是 ▲ .
5.若复数![]() ,
,![]() ,
,![]() ,且
,且![]() 与
与![]() 均为实数,
均为实数,
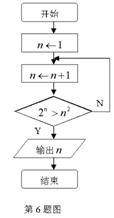 则
则![]()
▲ .
▲ .
6. 右边的流程图最后输出的![]() 的值
的值
是 ▲ .
7.若实数![]() 、
、![]() {
{![]() ,
,![]() ,
,![]() ,
,![]() },且
},且![]() ,则曲线
,则曲线![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的概率是
▲ .
轴上的双曲线的概率是
▲ .
8. 已知下列结论:
① ![]() 、
、![]() 都是正数
都是正数![]()
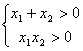 ,
,
② ![]() 、
、![]() 、
、![]() 都是正数
都是正数![]()
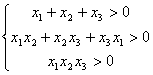 ,
,
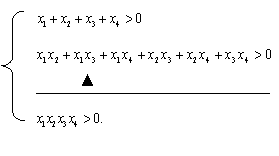 则由①②猜想:
则由①②猜想:
![]() 、
、![]() 、
、![]() 、
、![]() 都是正数
都是正数![]()
9.某同学五次考试的数学成绩分别是120, 129, 121,125,130,则这五次考试成绩
 的方差是 ▲ .
的方差是 ▲ .
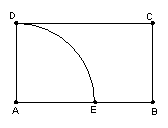
10.如图,在矩形![]() 中,
中,![]() ,
,![]() ,以
,以
![]() 为圆心,1为半径作四分之一个圆弧
为圆心,1为半径作四分之一个圆弧![]() ,在圆弧
,在圆弧![]()
上任取一点![]() ,则直线
,则直线![]() 与线段
与线段![]() 有公共点的概率
有公共点的概率
是 ▲ .
第10题图
11.用一些棱长为1cm的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图,则这个几何体的体积最大是 ▲ cm3.
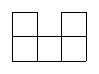
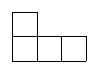
图1(俯视图) 图2(主视图)
第11题图
12.下表是某厂1~4月份用水量(单位:百吨)的一组数据,
| 月份 | 1 | 2 | 3 | 4 |
| 用水量 | 4.5 | 4 | 3 | 2.5 |
由其散点图可知,用水量![]() 与月份
与月份![]() 之间有较好的线性相关关系,其线性回归方程
之间有较好的线性相关关系,其线性回归方程
是 ▲ .
13.已知![]() 平面内一区域
平面内一区域![]() ,命题甲:点
,命题甲:点![]() ;命题乙:点
;命题乙:点
![]() .如果甲是乙的充分条件,那么区域
.如果甲是乙的充分条件,那么区域![]() 的面积的最小值是
▲ .
的面积的最小值是
▲ .
14.设![]() 是椭圆
是椭圆![]() 上任意一点,
上任意一点,![]() 和
和![]() 分别是椭圆的左顶点和右焦点,
分别是椭圆的左顶点和右焦点,
则![]() 的最小值为
▲ .
的最小值为
▲ .
二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.)
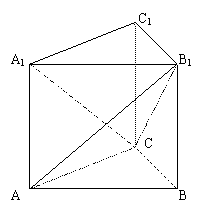 15.(本小题满分14分)
15.(本小题满分14分)
直三棱柱![]() 中,
中,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
16.(本小题满分14分)
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备![]() 年的年平均污水处理费用
年的年平均污水处理费用![]() (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
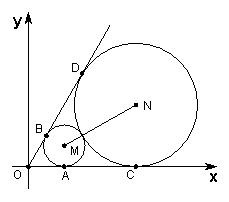 17.(本小题满分14分)
17.(本小题满分14分)
如图,已知圆心坐标为![]() 的圆
的圆![]() 与
与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点,另一圆
两点,另一圆![]() 与圆
与圆![]() 外切、且与
外切、且与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点.
两点.
(1)求圆![]() 和圆
和圆![]() 的方程;
的方程;
(2)过点B作直线![]() 的平行线
的平行线![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得的弦的长度.
截得的弦的长度.
18.(本小题满分14分)
已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 内的单调递增区间;
内的单调递增区间;
(2)若函数![]() 在
在![]() 处取到最大值,求
处取到最大值,求![]() 的值;
的值;
(3)若![]() (
(![]() ),求证:方程
),求证:方程![]() 在
在![]() 内没有实数解.
内没有实数解.
(参考数据:![]() ,
,![]() )
)
19.(本小题满分16分)
已知函数![]() (
(![]() )的图象为曲线
)的图象为曲线![]() .
.
(1)求曲线![]() 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(2)若曲线![]() 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线![]() 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(3)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
20.(本小题满分18分)
已知数列![]() 的通项公式是
的通项公式是![]() ,数列
,数列![]() 是等差数列,令集合
是等差数列,令集合![]() ,
,![]() ,
,![]() .将集合
.将集合![]() 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前5项成等比数列,且
的前5项成等比数列,且![]() ,
,![]() ,求满足
,求满足![]()
的正整数![]() 的个数.
的个数.
B.附加题部分
三、附加题部分(本大题共6小题,其中第21和第22题为必做题,第23~26题为选做题,请考生在第23~26题中任选2个小题作答,如果多做,则按所选做的前两题记分.解答应写出文字说明,证明过程或演算步骤.)
21.(本小题为必做题,满分12分)
已知直线![]() 被抛物线
被抛物线![]() 截得的弦长
截得的弦长![]() 为20,
为20,![]() 为坐标原点.
为坐标原点.
(1)求实数![]() 的值;
的值;
(2)问点![]() 位于抛物线弧
位于抛物线弧![]() 上何处时,△
上何处时,△![]() 面积最大?
面积最大?
22.(本小题为必做题,满分12分)
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为![]() ,求随机变量
,求随机变量![]() 的期望
的期望![]() .
.
23.(本小题为选做题,满分8分)
如图,在△![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于
于![]() .
.
(1)求![]() 的值;
的值;
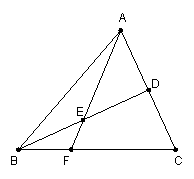 (2)若△
(2)若△![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
24.(本小题为选做题,满分8分)
已知直线![]() 的参数方程:
的参数方程:![]() (
(![]() 为参数)和圆
为参数)和圆![]() 的极坐标方程:
的极坐标方程:
![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)判断直线![]() 和圆
和圆![]() 的位置关系.
的位置关系.
25.(本小题为选做题,满分8分)
试求曲线![]() 在矩阵MN变换下的函数解析式,其中M =
在矩阵MN变换下的函数解析式,其中M =![]() ,N =
,N =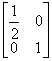 .
.
26.(本小题为选做题,满分8分)
用数学归纳法证明不等式:![]() .
.