高三数学第二学期调研测试
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.
注意事项:
答题前,考生务必将学校、姓名、班级、学号写在答卷纸的密封线内.选择题答案按要求填涂在答卷纸上;非选择题的答案写在答卷纸上对应题目的答案空格内,答案不写在试卷上.考试结束,将答卷纸收回.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=CPk(1-P)n![]() k.
k.
第Ⅰ卷(选择题 共50分)
一、选择题:每题5分
1、已知![]() 为实数,集合
为实数,集合![]() ,
,![]() ,
,![]() 表示把
表示把![]() 中的元素
中的元素![]() 映射到集合
映射到集合![]() 中仍为
中仍为![]() ,则
,则![]() 等于
( )
等于
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2、已知:![]() 是直线,
是直线,![]() 是平面,给出下列四个命题:(1)若
是平面,给出下列四个命题:(1)若![]() 垂直于
垂直于![]() 内的两条直线,则
内的两条直线,则![]() ;(2)若
;(2)若![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;(3)若
内的所有直线;(3)若![]() 且
且![]() 则
则![]() ;(4)若
;(4)若![]() 且
且![]() 则
则![]() ;(5)若
;(5)若![]() 且
且![]() 则
则![]()
![]() 。
。
其中正确命题的个数是
A.0 B. 1 C. 2 D. 3
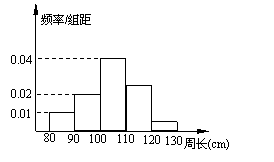 3、为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如右),
3、为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如右),
那么在这100株树木中,底部周长小于
的株数是
A.30 B.60
C.70 D.80
4、若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
| x | -2 | 0 |
|
| 0.592 | 1 |
则不等式![]() (x)<0的解集为
( )
(x)<0的解集为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
5、数列{an}满足:a1 = 1,且对任意的![]() 都有:
都有:![]() ,则
,则
![]() =( )
=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、已知sinx-siny= -![]() ,cosx-cosy=
,cosx-cosy= ![]() ,且x,y为锐角,则tan(x-y)的值是 ( )
,且x,y为锐角,则tan(x-y)的值是 ( )
A.![]() B.-
B.-![]() C.±
C.±![]() D.
D.![]()
7、已知抛物线的方程为y2=2px (p>0), 且抛物线上各点与焦点距离的最小值为2, 若点M在此抛物线上运动, 点N与点M关于点A(1, 1)对称, 则点N的轨迹方程为 ( )
A. x2=8y B. (x-2)2=8(y-2) C. (y-2)2=-8(x-2) D. (y-2)2=8(x-2)
8、已函数f(x)=
x2+2xf '(1), 则曲线y=f(x)在![]() 处的切线方程为
( )
处的切线方程为
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
9、已知![]() 中 ,角
中 ,角![]() 的对边分别为
的对边分别为![]() ,
,![]() 为
为![]() 边上有高,以下结论:①
边上有高,以下结论:①![]() ;②
;②![]() 为锐角三角形③
为锐角三角形③![]()
![]() ④
④![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1 B.2 C.3 D.4
10、已知![]() 是定义在
是定义在![]() 上的不恒为零的函数,且对于任意的
上的不恒为零的函数,且对于任意的![]() 、
、![]() ,满足
,满足![]()
![]() ,
,![]() ,
,![]() (
(![]() ),
),![]() (
(![]() )。考查下列结论:①
)。考查下列结论:①![]() ;②
;②![]() 为偶函数;③数列
为偶函数;③数列![]() 为等比数列;④
为等比数列;④![]() 为等差数列。其中正确的是
( )
为等差数列。其中正确的是
( )
A、①②③ B、①③④ C、③④ D、①③
二、填空题:每题5分
11、设集合A=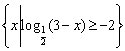 ,B=
,B=![]() ,若A∩B≠
,若A∩B≠![]() ,则实数a的取值范围___________________________。
,则实数a的取值范围___________________________。
12、三棱锥![]() 中,
中,![]() 平面ABC,
平面ABC,![]() ,若
,若![]() ,则该三棱锥外接球的体积是 .
,则该三棱锥外接球的体积是 .
13、按下列程序框图来计算:

如果x=5,应该运算 次才停止。
14、三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲方手中的概率为 .
15、直线![]() 过点
过点![]() ,若可行域
,若可行域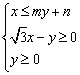 的外接圆直径为
的外接圆直径为![]() .则实数n的值是
.
.则实数n的值是
.
16、对于函数f(x)=x2(x>0)图象上任意两点A(a,a2),B(b,b2),直线段AB必在曲线段AB的上方,设点C分![]() 的比为
的比为![]() ,则由图象的特征可得不等式
,则由图象的特征可得不等式![]() .请分析y=lgx的图象特征,类比上述不等式可以得到
.请分析y=lgx的图象特征,类比上述不等式可以得到
三、解答题:
17、田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1、A2、A3;田忌的三匹马B1、B2、B3;三匹马各比赛一次,胜两场者为获胜,双方均不知对方的马出场顺序。
(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3;则田忌获胜
的概率是多大?
(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3;则田忌获胜
的概率是多大?
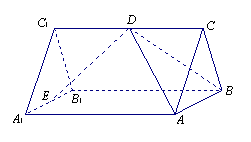 18、(本题满分15分)如图,已知
18、(本题满分15分)如图,已知![]() 是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱
是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求直线![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的大小.
的大小.
19、(本题满分14分)已知数列{a n}前n项的和为S n,前n项的积为![]() ,且满足
,且满足![]() 。
。
①求![]() ;
②求证:数列{a n}是等比数列;
;
②求证:数列{a n}是等比数列;
③是否存在常数a,使得![]() 对
对![]() 都成立?
都成立?
若存在,求出a,若不存在,说明理由。
20、(本小题满分14分)飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
 (3)若信号从P点的正上方Q点处发出,则A、B收到信号的时间差变大还是变小,并证明你的结论.
(3)若信号从P点的正上方Q点处发出,则A、B收到信号的时间差变大还是变小,并证明你的结论.
21、(本题满分15分)已知函数![]() ,
,![]() ,
,![]()
![]() 的最小值恰好是方程
的最小值恰好是方程![]() 的三个根,其中
的三个根,其中![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)设![]() ,
,![]() 是函数
是函数![]() 的两个极值点.
的两个极值点.
①若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
②求![]() 的取值范围.
的取值范围.
数学试题参考答案
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | C | D | D | B | C | A | B | B |
二、 填空题:
11、 ![]() ; 12、
; 12、 ![]() ;
13、4;
;
13、4;
14、 ![]() ; 15、 8 ; 16、
; 15、 8 ; 16、![]()
三、解答题:本大题共5小题,共70分
17、田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1、A2、A3;田忌的三匹 马B1、B2、B3;三匹马各比赛一次,胜两场者为获胜,双方均不知对方的马出场顺序。
(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3;则田忌获胜
的概率是多大?
(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3;则田忌获胜
的概率是多大?
17、(1)解:田忌获胜的概率是![]() ;
;
(2)解:田忌获胜的概率是![]() 。
。
18、 如图,已知
如图,已知![]() 是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱
是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求直线![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的大小.
的大小.
18、 (1)证明:连结C1E,则C1E^A1B1,
又∵A1B1^C1C,∴A1B1^平面EDC1,∴A1B1^DE,
而A1B1//AB,∴AB^DE. ·········································································5分
(2)取AB中点为F,连结EF,DF,则EF^AB,∴AB^DF.
过E作直线EH^DF于H点,则EH^平面DAB,∴EH就是直线A1B1到平面DAB的距离.
在矩形C1EFC中,∵AA1=AB=2,∴EF=2,C1E=,DF=2,
∴在△DEF中,EH=,
故直线A1B1到平面DAB的距离为. ···············································10分
(3)过A作AM^BC于M点,则AM^平面CDB,
过M作MN^BD于N点,连结AN,则AN^BD,∴∠ANM即为所求二面角的平面角,
在Rt△DCB中,BC=2,DC=1,M为BC中点,∴MN=,
在Rt△AMN中,tan∠ANM=,
故二面角A-BD-C的大小为arctan. ··············································15分
19、(本题满分14分)已知数列{a n}前n项的和为S n,前n项的积为![]() ,且满足
,且满足![]() 。
。
①求![]() ;
②求证:数列{a n}是等比数列;
;
②求证:数列{a n}是等比数列;
③是否存在常数a,使得![]() 对
对![]() 都成立?
都成立?
若存在,求出a,若不存在,说明理由。
19、①![]() ;③
;③![]()
 20、(本小题满分14分)飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
20、(本小题满分14分)飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
(3)若信号从P点的正上方Q点处发出,则A、B收
到信号的时间差变大还是变小,并证明你的结论.
20、 解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则
![]() 则
则![]()
即A、C两个救援中心的距离为![]()
(2)![]() ,所以P在BC线段的垂直平分线上
,所以P在BC线段的垂直平分线上
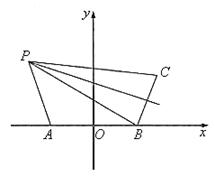 又
又![]() ,所以P在以A、B为焦点的双曲线的左支上,且
,所以P在以A、B为焦点的双曲线的左支上,且![]()
∴双曲线方程为![]()
BC的垂直平分线的方程为![]()
联立两方程解得:![]()
![]()
∴∠PAB=120°所以P点在A点的北偏西30°处
(3)如图,设![]()
![]()
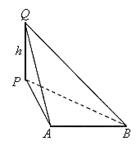
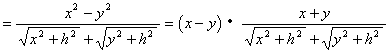
又∵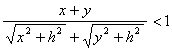
![]()
![]()
即A、B收到信号的时间差变小
21、(本题满分14分)已知函数![]() ,
,![]() ,
,![]()
![]() 的最小值恰好是方程
的最小值恰好是方程![]() 的三个根,其中
的三个根,其中![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)设![]() ,
,![]() 是函数
是函数![]() 的两个极值点.
的两个极值点.
①若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
②求![]() 的取值范围.
的取值范围.
21、解:(Ⅰ)三个函数的最小值依次为![]() ,
,![]() ,
,![]() ,…………………… …3分
,…………………… …3分
由![]() ,得
,得![]()
∴ ![]()
![]() ,
,
故方程![]() 的两根是
的两根是![]() ,
,![]() .
.
故![]() ,
,![]() .………………………4分
.………………………4分
![]() ,即
,即![]()
∴ ![]() . …………………………………………………………5分
. …………………………………………………………5分
(Ⅱ)①依题意![]() 是方程
是方程![]() 的根,
的根,
故有![]() ,
,![]() ,
,
且△![]() ,得
,得![]() .
.
由![]() ………………………7分
………………………7分
![]()
![]() ;得,
;得,![]() ,
,![]() .
.
由(Ⅰ)知![]() ,故
,故![]() ,
,
∴ ![]() ,
,![]()
∴ ![]() .…………………………………………9分
.…………………………………………9分
②![]()
![]()
![]()
![]()
![]() (或
(或![]() ). ………………………………………11分
). ………………………………………11分
由(Ⅰ)![]()
∵ ![]() ,
,
∴ ![]() ,
,
又![]() ,
,
∴ ![]() ,
,
![]() ,
,![]() (或
(或![]() ) …………………13分
) …………………13分
∴ ![]() .…………………………………15分
.…………………………………15分