高三数学第二次联考试题卷
数 学(理工类)
命题者:南县一中:陈敬波、沅江一中:朱清明、长炼中学:吴湘波.
考试时量:120分钟,试卷满分:150分.
 参考公式:
参考公式:
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集U = {1,2,3,4,5,6,7},A = {3,4,5},B = {1,3,6},则A∩(![]() )等于 ( )
)等于 ( )
A.{4,5} B.{2,4,5,7}
C.{1,6} D.{3}
2. 若![]() 、
、![]() 是两条不重合直线,
是两条不重合直线,![]() 、
、![]() 是两个不重合的平面,则
是两个不重合的平面,则![]() ∥
∥![]() 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
(A)![]() ,
,![]() ,
,![]() ∥
∥![]() 且b∥
且b∥![]() (B)
(B)![]() ,
,![]() ,且a∥b
,且a∥b
(C)![]() ,
,![]() ,且
,且![]() ∥
∥![]() (D)
(D)![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,且a∥b
,且a∥b
3. 在等差数列![]() 中,
中,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的最小值为( )
的最小值为( )
(A)60 (B)62 (C)70 (D)72
4. 已知![]() ,
,![]() ,且满足
,且满足![]() ,则下列不等式恒成立的是( )
,则下列不等式恒成立的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.以直线y= -x+1与坐标轴的交点为焦点的抛物线的标准方程为( )
A x2=4y或y2=4x B x2=2y或y2=2x
C x2=-4y或y2=-4x D x2=2y或y2=-2x
6.定义: a × b = a b sin![]() ,其中
,其中![]() 为向量a与b的夹角,若 a = 2, b = 5,a · b = – 6,则 a × b =( )
为向量a与b的夹角,若 a = 2, b = 5,a · b = – 6,则 a × b =( )
A.-8 B. 8 C.8或 – 8 D.6
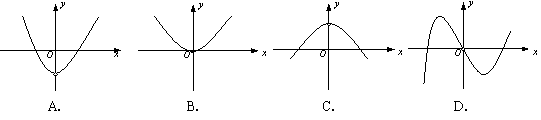
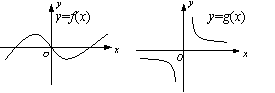 7.已知
7.已知![]() 与
与![]() 的图象如图所示,
的图象如图所示,
则函数![]() 的图象可以是
的图象可以是
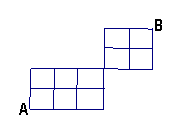 8.在某城市中,A、B两地有如右图所示道路网,从A地到B地最近的走法有( )种
8.在某城市中,A、B两地有如右图所示道路网,从A地到B地最近的走法有( )种
A 25 B ![]() C
C ![]() D
D ![]()
9.一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为1,![]() ,3,则这个三棱锥的外接球的表面积为( )
,3,则这个三棱锥的外接球的表面积为( )
(A) 16π (B) 32π (C) 36π (D) 64π
10.定义在R上的函数f(x),给出下列四个命题:
① 若f(x)是偶函数,则f(x+3)的图象关于直线x=-3对称;
② 若f(x+3)=-f(3-x),则f(x)的图象关于点(3,0)对称;
③ 若f(x+3)是偶函数,则f(x)的图象关于直线x=3对称;
④ y=f(x+3)与y=f(3-x)的图象关于直线x=3对称.
其中正确命题的个数有( )
A 0 B 1 C 2 D 3
试题卷 第 Ⅱ 卷 (非选择题,共100分)
二、填空题:本大题共5小题,每小题5分,共25分。将正确答案填在答题卷上对应题号的横线上。
11.设i是虚数单位,则![]() 的虚部为 。
的虚部为 。
12. 已知变量![]() 、
、![]() 满足
满足![]() 则
则![]() 的最大值为__________。
的最大值为__________。
13.若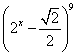 的展开式的第7项为
的展开式的第7项为![]() ,则
,则![]()
![]()
14. 已知![]() 服从正态分布N(5,4),那么P(
服从正态分布N(5,4),那么P(![]() )=____________.
)=____________.
15. 对于一切实数x,令[x]为不大于x的最大整数,则函数![]() 称为高斯函数或取整函数,如 f(2.1)=2;若
称为高斯函数或取整函数,如 f(2.1)=2;若![]() 为数列
为数列![]() 的前n项和,则
的前n项和,则![]() =____________.
=____________.
三、解答题:本大题共6小题,满分80分。解答应写出文字说明,证明过程或演算步骤。
16.(本大题满分12分)
已知锐角△ABC中,三个内角为A、B、C,两向量![]() ,
,![]() ,若
,若![]() 与
与![]() 是共线向量,(1)∠A的大小;(2)求函数
是共线向量,(1)∠A的大小;(2)求函数![]() 取最大值时,∠B的大小
取最大值时,∠B的大小
17. (本大题满分13分)
有A,B,C,D四个城市,它们都有一个著名的旅游点依此记为a,b,c,d把A,B,C,D和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连接一个城市与该城市的旅游点正确的得2分,连错的得0分;
(1)求该爱好者至少得2分的概率; (2)求所得分的数学期望?
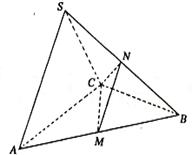 18.(本大题满分13分) 在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
18.(本大题满分13分) 在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2![]() ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(1)证明:AC⊥SB;
(2)求二面角N—CM—B的大小;
(3)求点B到平面CMN的距离.
19.(本大题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设![]() 表示学生注意力随时间t (分钟)的变化规律(
表示学生注意力随时间t (分钟)的变化规律(![]() 越大,表明学生注意力越集中),经过实验分析得知:
越大,表明学生注意力越集中),经过实验分析得知:
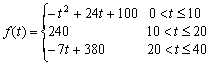
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过
适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
20.(本大题满分14分)
已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为A,P是椭圆
,右顶点为A,P是椭圆![]() 上任意一点,设该双曲线
上任意一点,设该双曲线![]() :以椭圆
:以椭圆![]() 的焦点为顶点,顶点为焦点,B是双曲线
的焦点为顶点,顶点为焦点,B是双曲线![]() 在第一象限内的任意一点,且
在第一象限内的任意一点,且![]() 。
。
(1)设![]() 的最大值为
的最大值为![]() ,求椭圆离心率;(2)若椭圆离心率
,求椭圆离心率;(2)若椭圆离心率![]() 时,证明:总有
时,证明:总有![]() 成立。
成立。
21.(本大题满分14分)
已知函数![]() (a为实常数).
(a为实常数).
(1) 当a = 0时,求![]() 的最小值;
的最小值;
(2)若![]() 在
在![]() 上是单调函数,求a的取值范围;
上是单调函数,求a的取值范围;
(3)设各项为正的无穷数列![]() 满足
满足![]() 证明:
证明:![]() ≤1(n∈N*).
≤1(n∈N*).
参考答案:
一.1、A,2、C,3、B,4、D,5、C,6、B,7、A,8、C,9、A,10、D
二.11、-3;.12、1;13、![]() 14、
14、![]() 15、
15、![]()
三.
16.解:
![]() ……(2’)
……(2’)
整理得:![]() ……………………………(4’)
……………………………(4’)
又A为锐角,![]() …………………(6’)
…………………(6’)
(2)由(1)知![]() ………………………(7’)
………………………(7’)
故
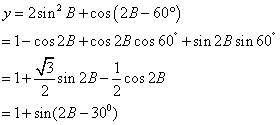
……………………………(12’)
当B=600时,Y取得最大值。……………………(13’)
17. 设答对题的个数为y,得分为![]() ,y=0,1,2,4
,
,y=0,1,2,4
,![]() =0,2,4,8………(1’)
=0,2,4,8………(1’)
∵![]() ,
, ![]() ,
,
|
则![]() 的分布列为
的分布列为
…………………………………10分
(2)E![]() =
=![]() …………………………12分
…………………………12分
答:该人得分的期望为2分……………………………………………………13分
18. 解:(1)取AC中点D,连结SD、DB.
∵SA=SC,AB=BC,
∴AC⊥SD且AC⊥BD,
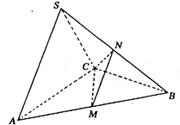 ∴AC⊥平面SDB,又SB
∴AC⊥平面SDB,又SB![]() 平面SDB,
平面SDB,
∴AC⊥SB-----------4分
(2)∵AC⊥平面SDB,AC![]() 平面ABC,
平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连结NF,
则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角---------------6分
∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC.
又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,
∴NE=![]() SD=
SD=![]() =
=![]()
![]()
![]() =
=![]() ,
且ED=EB.
,
且ED=EB.
在正△ABC中,由平几知识可求得EF=![]() MB=
MB=![]() ,
,
在Rt△NEF中,tan∠NFE=![]() =2
=2![]() ,
,
∴二面角N—CM—B的大小是arctan2![]() -----------------------8分
-----------------------8分
(3)在Rt△NEF中,NF=![]() =
=![]() ,
,
∴S△CMN=![]() CM·NF=
CM·NF=![]()
![]() ,
,
S△CMB=![]() BM·CM=2
BM·CM=2![]() -------------11分
-------------11分
设点B到平面CMN的距离为h,
∵VB-CMN=VN-CMB,NE⊥平面CMB,
∴![]() S△CMN·h=
S△CMN·h=![]() S△CMB·NE,∴h=
S△CMB·NE,∴h=![]() =
=![]() .
.
即点B到平面CMN的距离为![]() --------13分
--------13分
19. (1)解:当0<t≤10时,
![]() 是增函数,且
是增函数,且![]() 3分
3分
当20<t≤40时,![]() 是减函数,且
是减函数,且![]() 6分
6分
所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟 7分
(2)解:![]() ,所以,讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中 9分
,所以,讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中 9分
(3)当0<t≤10时,令![]() 得:
得:![]() 10分
10分
当20<t≤40时,令![]() 得:
得:![]() 12分
12分
则学生注意力在180以上所持续的时间![]()
所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题 14分
20.解:
(1)设![]() 又
又![]()
![]()
又![]() 得
得![]()
![]()
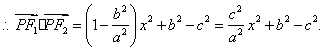
当![]() 时
时![]() 最大值为
最大值为![]() 。故
。故![]()
![]() ………………………(6’)
………………………(6’)
(2)由椭圆离心率![]() 得双曲线
得双曲线
![]()
设![]() 则
则![]() ……………(7’)
……………(7’)
① 当AB⊥x轴时,![]()
![]() .…………(9’)
.…………(9’)
②当![]() 时.
时.
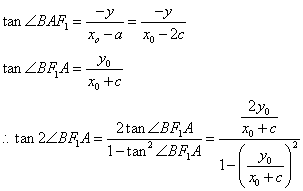
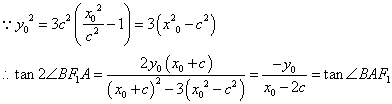
………………………………………………(12’)
又![]() 与
与![]() 同在
同在![]() 或
或![]() 内……………(13’)
内……………(13’)
![]() =
=![]()
总![]() =
=![]() 有成立。…………………………(14’).
有成立。…………………………(14’).
21. (1)![]()
当a≥0时,![]() 在[2,+∞)上恒大于零,即
在[2,+∞)上恒大于零,即![]() ,符合要求; 2分
,符合要求; 2分
当a<0时,令![]() ,g (x)在[2,+∞)上只能恒小于零
,g (x)在[2,+∞)上只能恒小于零
故△=1+4a≤0或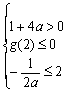 ,解得:a≤
,解得:a≤![]()
∴a的取值范围是![]() 6分
6分
(2)a = 0时,![]()
当0<x<1时![]() ,当x>1时
,当x>1时![]() ,∴
,∴![]() 8分
8分
(3)反证法:假设x1 = b>1,由![]() ,
,
∴![]()
故![]()
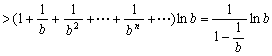 ,即
,即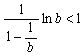 ①
①
又由(2)当b>1时,![]() ,∴
,∴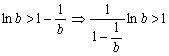
与①矛盾,故b≤1,即x1≤1
同理可证x2≤1,x3≤1,…,xn≤1(n∈N*) 14分