高三数学第二次诊断性考试
高三数学试题（理科）
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间120
分钟。
2．考生一律不准使用计算器。
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设集合P={1，2，3，4，5}，集合
，那么下列结论正确的是（ ）
A．
B．
C．
D．
2．“p或q”为真命题，“p且q为真命题”的 （ ）
A．充分不必要条件 B．必要非充分条件
C．充要条件 D．即不充分也不必要条件
3．下列不等式中解集为实数集R的是 （ ）
A．
B．
C．
D．
4．已知两点M（－2，0），N（2，0），点P满足
，则点P的轨迹方程为（ ）
A．
B．
C．
D．
5．设
则此四个数
中最大的是 （ ）
A．b B．
C．2ab D．
6．已知圆中一段弧长正好等于该圆的外切正三角形的边长，则这段弧所对圆心角的度数为
（ ）
A．
B．
C．
D．
7．设函数
是定义在R上的奇函数，若
，则a的取值范围是
（ ）
A．
B．且
C．
且
D．－1<
8．若函数是定义在（0，+
）上的增函数，且对一切x>0,y>0满足
，则不等式
的解集为 （ ）
A．（－8，2） B．（2，+） C．（0，2） D．（0，+）
9．已知三个互不相等的实数a、b、c成等差数列，那么关于x的方程
（ ）
A．一定有两个不相等的实数根 B．一定有两个相等的实数根
C．一定没有实数根 D．一定有实数根
|
的导数
处取到极大值，则a的取值范围是 （ ）
A．（－，－1） B．（－1，0） C．（0，1） D．（0，+）
11．设O是△ABC内部一点，且
的面积之比为（ ）
A．2 B． C．1 D．
12．已知等差数列
的前n项和为An，等差数列
的前n项和为Bn，且
，则使
为整数的所有n的值的个数为 （ ）
A．1 B．2 C．3 D．4
|
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13．若直线
和直线
垂直，则a的值是
。
14．已知实数x,y满足不等式组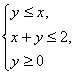
那么目标函数
的最大值是
。
15．在数列中，已知
，这个数列的通项公式是
= 。
16．设x,y
的最小值为
。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分10分）已知集合
（1）若
，求a的取值范围；
（2）若
，求a的取值范围。
18．（本小题满分12分）已知函数
（1）求的单调递减区间；
（2）若在区间[－2，2]上的最大值为20，求它在该区间上的最小值。
19．（本小题满分12分）解关于x的不等式
20．（本小题满分12分）已知函数的前项a1=1，其前n项和为Sn，且对任意正整数n，有n，
成等差数列。
（1）求证：数列
成等比数列；
（2）求数列的通项公式。
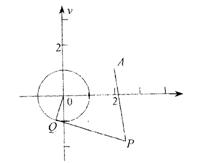
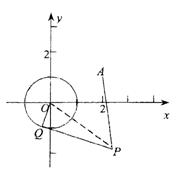
21．（本小题满分14分）已知⊙
由⊙O外一点P（a,b）向⊙O引切线PQ，切点为Q，且满足
（1）求实数a,b间满足的等量关系；
（2）求线段PQ长的最小值；
|
22．（本小题满分14分）已知二次函数
同时满足：①不等式
的解集有且只有一个元素；②在定义域内存在
，使得不等式
成立。设数列的前n项和
。
（1）求函数的表达式；
（2）求数列的通项公式；
（3）设各项均不为零的数列
中，所有满足
的整数I的个数称为这个数列的变号数。令
（n为正整数），求数列的变号数。
高三数学第二次诊断性考试
数学试题（理科）参考答案
|
1—6 CBABA 7—12 ADCDBCD
二、填空题
13．0或
； 14．4； 15．
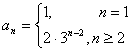16．
三、解答题
17．（本小题满分10分）
解：
（1）
a<0时，
a=0时
显然不符合条件。
……………………6分
（2）要满足
时成立
∵此时B
故所求的a值为3。…………………………10分
18．（本小题满分12分）
解：（1）
令
……………………4分
所以函数的单调递减区间为（－，－1）和（3，+）………………5分
（2）因为
所以
…………………………7分
因为在（－1，3）上
>0，所以在[－1，2]上单调递增，
又由于在[－2，－1]上单调递减，
因此f（2）和f（－1）分别是在区间[－2，2]上的最大值和最小值…………10分
于是有22+a=20，解得a=－2。
故
因此f（－1）=1+3－9－2=－7，
即函数在区间[－2，2]上的最小值为－7。……………………12分
19．（本小题满分12分）
解：原不等式可化为
即
…………………………4分
当m>1时，
……………………6分
当m=1时，
…………………………8分
当0<m<1时，
……………………10分
当m≤0时，…………………………12分
20．（本小题满分12分）
解：（1）
为等差数列
…………………………2分
又
…………………………4分
即
…………………………6分
即
成等比数列……………………8分
（2）由（1）知
是以
为首项，2为公比的等比数列。
…………………………10分
又
………………………………12分
|
解：（1）连OP，
为切点，PQ⊥OQ，由勾股定理有
又由已知
即：
化简得实数a、b间满足的等量关系为：
…………………………5分
（2）由，得b=－2a+3 。
故当
，即线段PQ长的最小值为
………………10分
（3）设⊙P的半径为R，
OP设⊙O有公共点，⊙O的半径为1，
而
故当
得半径取最小值⊙P的方程为
……………………14分
本题其它解法参照以上标准酌情给分。
22．解（1）
的解集有且只有一个元素，
当a=4时，函数
上递减
故存在，使得不等式成立
当a=0时，函数
上递增
故不存在，使得不等式成立
综上，得a=4，
…………………………5分
（2）由（1）可知
当n=1时，
当
时，
…………………………10分
（3）由题设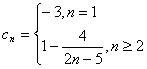
，
递增，
即
时，有且只有1个变号数；
又
∴此处变号数有2个。
综上得数列的变号数为3。………………14分